The Improving Mathematics Education in Schools (TIMES) Project
By year seven, students are expected to have developed almost all of the whole number arithmetic concepts outlined in the modules:
Using Place Value to Write Numbers
Multiplication of Whole Numbers
The purpose of this module is to bring together the ideas presented in the above modules for the teachers of the first year of secondary school mathematics. Students need to have a sound understanding of whole numbers, including the arithmetic of whole numbers, before they move onto other topics, and in particular algebra.
There is some repetition of material from the modules mentioned above but here it is brought together not only for the convenience of the reader but also for the purpose of presenting a more holistic view.
Order of operations is an important section of this module and does not appear in any of the above modules.
Addition
Of the four arithmetic operations on numbers, addition is the most natural. The ability to add numbers in your head is used in everyday life, when you play or watch sport and when you go shopping.
Subtraction
Subtraction answers questions such as:
- 1
- A class has 30 students and 16 of them are girls. How many boys are there in the class?
- 2
- I have $100 and I spend $20. How much do I have left?
- 3
- Terry has 11 chocolates and Marie has 7. How many more chocolates does Terry have?
These three questions are examples of three different types of question that require subtraction for their solution.
Multiplication
Examples of the use of multiplication include calculating the cost of six items costing 25 cents each. It is much quicker to calculate 6 × 25 by multiplication than by repeated addition. Multiplication answers questions such as:
- 1
- Judy brought 15 boxes of chocolates. Each box contained 24 chocolates. How many chocolates did Judy have?
- 2
- Henry has 16 rolls of wire. Each roll is 18 m long. What is the total length of wire that Henry has?
The natural geometric model of multiplication as rectangular area connects arithmetic to applications in measurement. Multiplication therefore provides an early link between arithmetic and geometry.
Division
Division is the last of the basic arithmetic operations to be introduced and, technically,
the most challenging. Division answers questions such as:
- 1
- How many apples will each friend get if four friends share 24 apples equally between them?
- 2
- If 421 children are going on an excursion and each bus can carry 35 children,
how many full buses are there and how many children are left over? - 3
- If you go out to dinner in a group of 12 and split the bill of $600 evenly, how much does each pay?
- 4
- If twenty pens are shared equally amongst seven children how many does each child receive, and how many are left over?
Division problems arise when we try to break up a quantity into groups of equal size and when we try to “undo” multiplications. Division is also central to the calculations of ratios, proportions, percentages and slopes.
The standard algorithms are useful when larger numbers make mental calculations difficult. While there are many ways to solve problems with arithmetic, the commonly taught algorithms have remained in constant use because they provide an accurate and efficient means for calculating with whole numbers.
Once we have developed an understanding of numbers, we can use calculators and computers with some confidence that we can identify any gross data-entry errors. A relatively common example of someone working without a sense of number is the person at the check-out who tries to charge you a large sum for an inexpensive item simply because the cash register tells them to, without pausing to think that perhaps
the code for the item was incorrect.
While there are many labour-saving devices that will do calculations, a person will not develop a number-sense or a fluency with arithmetic if they move to calculators too quickly. Students should have an opportunity to develop a number sense, then should be allowed to develop fluency with algorithms, and only then be allowed unrestricted use of calculators.
Since arithmetic is an essential tool in so many of the things we do, it is by no means an exaggeration to say that the development of a solid understanding of arithmetic is essential for future success. Without a secure mastery of arithmetic students will find algebra frustratingly difficult.
Students who start Year 7 without a familiarity with the basic operations should be given the opportunity to revisit earlier work.
Addition
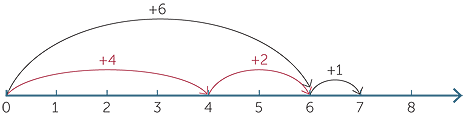
Addition can be modelled by combining objects and by jumps on the number line.
For example, the sum 24 + 5 + 10 can be modelled geometrically on the number line as

See also the module, Addition of Whole numbers.
Multiplication
Multiplication of whole numbers appears in the guise of
- Repeated addition, as in calculating 3 × 5 = 15 by writing 3 + 3 + 3 + 3 + 3
- Skip-counting, as in reciting 3, 6, 9, 12, 15
- Arrays and rectangular area, as in knowing that 3 × 5= 15 is the area of the rectangle
![]()

![]()

Rectangular area is the natural geometric model of multiplication and provides a good access point for visual learners.
See also the module, Multiplication of Whole Numbers.
Index notation
We use index notation to abbreviate products with multiple copies of the same factor. The use of indices shortens 2 × 2 × 3 × 3 × 5 × 5 × 5 × 5 to 22 × 32 × 54. In the expression 54, the number 5 is called the base and the number 4 is called the index.
The geometric model of multiplication provides a connection between indices and dimension. Just as multiplying two whole numbers corresponds to the area of a rectangle, multiplying three whole numbers corresponds geometrically to calculating the volume of a rectangular prism. So 52 = 5 × 5 is the area of a square of side length 5, and 53= 5 × 5 × 5 is the volume of a cube of side length 5.
By considering what happens when we multiply numbers together repeatedly, we establish that
- To multiply powers with the same base, add the indices.
![]() am × an =am + n
am × an =am + n
By considering what happens when we divide one power of a number by another we observe that
- To divide powers with the same base, subtract the indices, (where m > n)
![]() am ÷ an = am − n
am ÷ an = am − n
We also establish that
- To raise a power to a power, multiply the indices.
![]() (am)n = am×n
(am)n = am×n
By considering what happens when we multiply numbers with different bases but the same power, we observe that
- The power of a product is the product of the powers
![]() an × bn =(a × b)n
an × bn =(a × b)n
See also the module, Multiples, Factors and Powers
Subtraction
Subtraction is the inverse of addition and can be modelled geometrically on the number line. Subtraction appears in two slightly different guises
- as ‘take-away’, and
- as ‘difference’.
Typically, subtraction as a ‘take-away’ is calculated directly and modelled on the number line using a backwards jump. For example, we calculate 47 − 5 by taking five away from 47 in a single jump on the number line.

47 − 5 = 42
Subtraction as a difference is often calculated by complementary addition and modelled using a forward jump on the number line. For example, the difference between 47 and 42 can be calculated from the complementary addition 47 = 42 + 5 and modelled on the number line by noting that the jump from 42 to 47 is five units long.

47 = 42 + 5
See also the module, Subtraction of Whole Numbers.
Division
See also the module, Division of Whole Numbers.
Division always involves splitting something into a number of equal parts, but there are many contrasting situations that can all be described by ‘division’. In the expression
32 ÷ 6 we call 32 the dividend and 6 the divisor.
The mathematical development of division of whole numbers takes place in three stages:
- division without remainder,
- division with remainder, and
- division leading to a fraction or mixed numeral.
Division without remainder
In division without remainder, or exact division, the answer is a whole number.
An example of this is 30 ÷ 6 = 5. This type of division happens when the dividend is a whole-number multiple of the divisor, and is the inverse of multiplication of two whole numbers. The statement 30 ÷ 6 = 5 has the complementary multiplication 30 = 5 × 6.
Division with remainder
Division with remainder arises when the dividend is not an exact multiple of the divisor, as in the observation that 32 ÷ 6 is 5 with remainder 2. Arithmetically, this corresponds
to the statement
![]() 32 = 5 × 6 + 2.
32 = 5 × 6 + 2.
We write
![]()

Decompositions of the dividend using other multiples of the divisor, such as
32 = 6 × 6 − 4![]() or
or![]() 32 = 4 × 6 + 8,
32 = 4 × 6 + 8,
are avoided by the convention that the remainder always be a positive number less than the divisor. The general approach is as follows:
- Find the largest multiple of the divisor that is less than the dividend to calculate
the quotient. - Find the difference between that multiple of the divisor and the dividend to calculate the remainder.
Division without remainder can be regarded as division with remainder 0. Division with remainder involves only whole numbers and does not use fractions.
EXERCISE 1
The first 100 days of a US presidency are regarded as crucial. Express 100 days in weeks and days. Then write down the corresponding division statement and the corresponding product-and-sum statement.
Division leading to a fraction or mixed numeral
Division leading to a fraction or mixed numeral arises when we think of 32 ÷ 6 as the fraction  . So we could write 32 ÷ 6 =
. So we could write 32 ÷ 6 =  or 5
or 5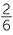 . We could also express our answer as a decimal.
. We could also express our answer as a decimal.
With fractions, division is the inverse of multiplication.
Division resulting in a mixed numeral requires an understanding of fractions, particularly cancelling fractions, because cancelling is often needed for the final result. It is therefore usual for students to learn division with remainder first, and then to learn division resulting in a mixed numeral in the course of learning fractions. It is important to understand, however, that both ways of expressing the answer are equally important, and both are required, depending on the problem.
EXERCISE 2
- a
- i
- How many days and hours in 60 hours?
- ii
- If a period of 60 hours is divided into 24 equal periods, how long is each period?
- b
- i
- How many 120 g packets can be made up from 2000g of coffee?
- ii
- If 2kg of coffee is divided into 120 packets, how much is in each packet?
- c
- i
- If hospitals cost $20 000 000 each, how many can be built with $208 000 000?
- ii
- If the Federal Government spends $208 000 000 on hospitals and pays for this from the money it receives from income tax, how much on average will it cost each of the 20 000 000 Australian citizens in taxes?
Laws of arithmetic and order of operations
The four arithmetic operations behave somewhat differently. The result of a list of calculations can vary depending on the order in which the calculations are performed. Care must therefore be taken to avoid ambiguity. We will discuss the conventions in detail later, but a general principle is that parentheses override all conventions and are always performed first, from the inside out.
Laws of arithmetic
Commutative laws
Addition and multiplication are both commutative. This mean that
![]() a + b = b + a and a × b = b × a for every pair of whole numbers a and b.
a + b = b + a and a × b = b × a for every pair of whole numbers a and b.
Commutativity means that we do not have to worry about whether we calculate
![]() a + b or b + a because the answer is the same.
a + b or b + a because the answer is the same.
Similarly, calculating a × b and b × a gives the same result.
Using the area model, commutativity of multiplication corresponds to rotating a rectangle through a right angle; so 3 × 5=5 × 3 is the observation that the area of the following rectangles is the same.
 |
 |
||
| 3 × 5 = 5 × 3 |
On the number line multiplication is modelled as repeated addition, so the fact that
3 × 5 = 5 × 3 is not so obvious because it is represented as 3 + 3 + 3 + 3 + 3 = 5 + 5 + 5.
Associative laws
Addition and multiplication are both associative. This means that
![]() a + (b + c)=(a + b)+c and a × (b × c) = (a × b) × c for every pair of whole numbers
a + (b + c)=(a + b)+c and a × (b × c) = (a × b) × c for every pair of whole numbers
![]() a, b and c.
a, b and c.
We can see associativity of addition on the number line. For example, in
4 + (2 + 1) = (4 + 2) + 1
![]() 4 + (2 + 1) corresponds to
4 + (2 + 1) corresponds to
![]()

whereas
![]() (4 + 2) + 1 corresponds to
(4 + 2) + 1 corresponds to
![]()
Associativity ensures that the expressions a + b + c and a × b × c are unambiguous, because it makes no difference which of the two operations is calculated first.
Any-order properties
The combination of commutativity and associativity lead to any-order principles for addition and multiplication.
The any-order property of addition
A list of numbers can be added two at a time in any order to calculate their sum.
The any-order property of multiplication
A list of numbers can be multiplied together in any order to calculate their product.
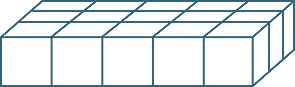
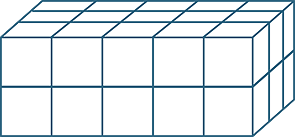
Multiplying three whole numbers corresponds geometrically to calculating the number of unit cubes in (or volume of) a rectangular prism. The any-order property of multiplication means that we can calculate this volume by multiplying the lengths of the sides in any order. The order of the calculation corresponds to slicing the volume up in different ways.
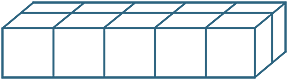 |
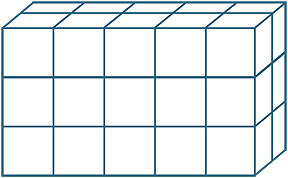 |
||
| 5 × 2 = 2 × 5 | (5 × 2) × 3 = (2 × 5) × 3 | ||
 |
 |
||
| 3 × 2 = 2 × 3 | (3 × 2) × 5 = (2 × 3) × 5 | ||
 |
 |
||
| 5 × 3 = 3 × 5 | (5 × 3) × 2 = (3 × 5) × 2 |
Subtraction and division
The commutative law does not hold for subtraction and division.
For example,
3 − 2 ≠ 2 − 3 and 3 ÷ 2 ≠ 2 ÷ 3.
The associative law does not hold for multiplication and division.
For example,
4 − (3 − 2) ≠ (4 − 3) − 2 and 4 ÷ (3 ÷ 2) ≠ (4 ÷ 3) ÷ 2.
Since subtraction and division are neither commutative nor associative, the result of a calculation depends on the order in which the operations are performed. This makes subtraction and division much less forgiving than addition and multiplication. Errors often occur when calculating subtractions or divisions because people erroneously transfer their intuition from addition and multiplication to the more badly-behaved operations of subtraction and division.
Order of Operations
The order in which operations are performed can also make a difference when operations are mixed, even if we are only combining addition and multiplication.
For example,
![]() 2 + (3 × 4) ≠ (2 + 3) × 4.
2 + (3 × 4) ≠ (2 + 3) × 4.
All ambiguity could be removed by using parentheses to indicate the order in which operations are to be performed. The following conventions are used to simplify
the appearance.
Order of operations
- Evaluate expressions inside brackets first.
- In the absence of brackets, carry out operations in the following order:
- powers
- multiplication and division from left to right
- addition and subtraction from left to right.
So 3 + 2 × 6 means 3 + (2 × 6).
Parenthetical calculations take priority because parentheses are used to override defaults. So, whereas 5 − 1 + 2 means (5 − 1) + 2, writing (5 + 1) × 2 forces us a change
in the order of operations. Similarly 5 + 1 × 2 means 5 + (1 × 2), and writing
(5 + 1) × 2 forces a change in the order of operations.
It is not wrong to include the parentheses in the expressions (5 − 1) + 2 and 5 + (1 × 2), even though they are not essential. Indeed, many mathematicians habitually put all parentheses in expressions without assuming any conventions.
EXAMPLE
Evaluate:
| a | 3 × 103 | b | 2 + 3 − 4 + 11 | |||
| c | 3 × 6 ÷ 2 + 6 | d | (9 − 6) × (11 − 5) | |||
| e | 42 ÷ 7 + 8 | f | 7 + 6 × (3 + 5 |
Solution
| a | 3 × 103 | = 3 × 1000 | b | 2 + 3 − 4 + 11 | = 5 − 4 + 11 | |||
| = 3000 | = 1 + 11 | |||||||
| = 12 |
| c | 3 × 6 ÷ 2 + 6 | = 18 ÷ 2 + 6 | d | (9 − 6) × (11 − 5) | = 3 × 6 | |||
| = 9 + 6 | = 18 | |||||||
| = 15 |
| e | 42 ÷ 7 + 8 | = 6 + 8 | f | 7 + 6 × (3 + 5) | = 7 + 6 × 8 | |||
| = 14 | = 7 + 48 | |||||||
| = 55 |
Distributivity
Commutativity and associativity are properties of a single operation. There is one final property that tells us how two operations interact and that is the key to expanding brackets. The equation 3 × (2 + 4) = (3 × 2) + (3 × 4) is an example of the distributivity of multiplication over addition. At the level of arrays, this corresponds to the following diagram.
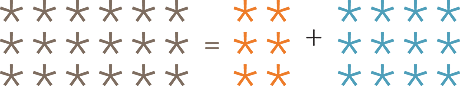
With areas it corresponds to the diagram below.
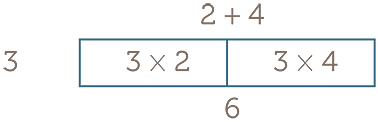
More generally,
![]() a × (b + c) = (a × b) + (a × c) for any numbers a, b and c.
a × (b + c) = (a × b) + (a × c) for any numbers a, b and c.
We can also distribute multiplication over addition from the right, so
![]() (a + b) × c = (a × c) + (b × c) for any numbers a,b and c.
(a + b) × c = (a × c) + (b × c) for any numbers a,b and c.
We can also distribute multiplication over subtraction from both the left and the right; so
![]() a × (b − c) = (a × b) − (a × c) and
a × (b − c) = (a × b) − (a × c) and
![]() (a − b) × c = (a × c) - (b × c) for any numbers a,b and c.
(a − b) × c = (a × c) - (b × c) for any numbers a,b and c.
All the above are called distributive laws
The distributivity of multiplication over addition and subtraction is the key to the multiplication and division algorithms.
We can distribute division over addition from the right, in the sense that
![]() (80 + 20) ÷ 8 = 80 ÷ 8 + 20 ÷ 8
(80 + 20) ÷ 8 = 80 ÷ 8 + 20 ÷ 8
Unfortunately we can’t distribute division over addition from the left in general.
For example,
![]() 80 ÷ (2 + 8) is not the same as (80 ÷ 2) + (80 + 8).
80 ÷ (2 + 8) is not the same as (80 ÷ 2) + (80 + 8).
This means that particular care must be taken when using the ÷ symbol for division rather than the alternative fraction notation. When deciding whether an operation distributes over division, it is worth thinking about the analogous statement expressed in the language of fractions. The equality
![]() (80 + 20) ÷ 8 = 80 ÷ 8 + 20 ÷ 8 corresponds to
(80 + 20) ÷ 8 = 80 ÷ 8 + 20 ÷ 8 corresponds to 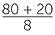 =
= 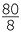 +
+ 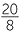
using fraction notation, whereas
![]() 80 ÷ (2 + 8) is
80 ÷ (2 + 8) is 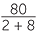 = 8 and (80 ÷2 ) + (80 + 8) is
= 8 and (80 ÷2 ) + (80 + 8) is 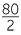 +
+ 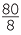 = 50
= 50
A proper understanding of distributivity and its limitations is crucial for algebra.
Basic mental strategies are covered in earlier modules on arithmetic. At this stage it is important to ensure students have achieved fluency with the basic addition and multiplication facts if they are to be able to implement the algorithms correctly and quickly. The reader is referred to the modules mentioned in the Assumed Knowledge section for further information.
Tables
Automatised knowledge of the addition and multiplication facts in the basic tables is an enormous advantage.
Addition Table
Knowledge of the addition table shown below is essential.

If students can add a single-digit number to a two-digit number, they can at least reconstruct their multiplication tables. It is therefore essential to ensure that students
can add fluently.
Multiplication Table
Fluency with the products in the multiplication table up to 10 × 10 are essential.
We strongly recommend that students learn their multiplication facts up to 12 × 12. This is primarily because the 12 times table is essential for time calculations — there are 12 months in a year, 24 hours in a day, and 60 minutes in an hour. Familiarity with dozens is useful in everyday life because packaging in 3 × 4 arrays is so much more convenient than in 2 × 5 arrays. In addition, the 12 × 12 table has many patterns that can be constructively exploited in pre-algebra exercises.
A straightforward approach to learning the tables is to recite each row, either by heart or by skip-counting. However, students also need to be able to recall individual facts without resorting to the entire table.
Looking at the 12 × 12 multiplication table gives the impression that there are 144 facts to be learnt. Ways of remembering the table are given in the module, Multiplication of the Whole Numbers.
Other Mental Strategies
Using the any-order properties
We often use the any-order properties in mental arithmetic, even when implementing the algorithms. For example, when calculating 71 + 68 + 49 + 32 most of us would naturally pair the tens complements to make the calculation easier:
| 71 + 68 + 49 + 32 | = (71 + 49) + (68 + 32) | |
| = 120 + 100 | ||
| = 220 |
We use the any-order property of multiplication to simplify calculations by changing the order in which we perform multiplications. For example,
| 2 × 2 × 2 × 5 × 5 × 5 | = (2 × 5) × (2 × 5) × (2 × 5) | |
| = 10 × 10 × 10 | ||
| = 1000 | ||
| 2 × 17 × 5 | = 10 × 17 | |
| =170 |
and
![]() 25 × 7 × 4 = 25 × 4 × 7 = 100 × 7 = 700.
25 × 7 × 4 = 25 × 4 × 7 = 100 × 7 = 700.
Sometimes this reordering happens after we decompose one of the factors, such as when we double twice in order to multiply by four, as in
![]() 17 × 4 = (17 × 2) × 2 = 34 × 2 = 68.
17 × 4 = (17 × 2) × 2 = 34 × 2 = 68.
This technique of moving a factor from one number to another in order to simplify a calculation has applications beyond repeated doubling, as in
![]() 36 × 5 = 18 × (2 × 5) = 180.
36 × 5 = 18 × (2 × 5) = 180.
Using the distributive property
We use the distributive property to enable us to reduce multiplication problems to a combination of familiar multiples. For example,
![]() 7 × 101 = 7 × (100 + 1) = 700 + 7 = 707,
7 × 101 = 7 × (100 + 1) = 700 + 7 = 707,
![]() 7 × 99 = 7 × (100 − 1) = 700 − 7 = 693,
7 × 99 = 7 × (100 − 1) = 700 − 7 = 693,
![]() 7 × 102 = 7 × (100 + 2) = 700 + 14 = 714,
7 × 102 = 7 × (100 + 2) = 700 + 14 = 714,
and
![]() 7 × 98 = 7 × (100 − 2) = 700 − 14 = 686.
7 × 98 = 7 × (100 − 2) = 700 − 14 = 686.
Some examples of this nature can be used to develop concepts needed in the formal algorithm. Observations such as 14 × 60 = 14 × 6 × 10 and 14 × 600 = 14 × 6 × 100 are fundamental to the implementation of the multiplication algorithm.
In addition, calculations such as
![]() 21 × 7 = 20 × 7 + 1 × 7 = 140 + 7 = 147
21 × 7 = 20 × 7 + 1 × 7 = 140 + 7 = 147
can be done first as a mental strategy, and then used as early examples in the formal algorithm. Other mental strategies related to the algorithm include observations such as
200 × 81 = 2 × 81 × 100 = 162 × 100 = 16 200,
where by multiplying by single-digit multiples of powers of ten is really no more complicated than multiplying by the single digit and keeping track of place value.
EXERCISE 3
Use the distributive law to carry out the following multiplications.
a ![]() 31 × 8
31 × 8 ![]() b
b ![]() 99 × 32
99 × 32 ![]() c
c ![]() 1001 × 34
1001 × 34 ![]() d
d ![]() 102 × 8
102 × 8
EXERCISE 4
The identity (a − b)(a + b) = a2 − b2 is also useful for mental computation.
For example: 49 × 51 = (50 − 1) × (50 + 1) = 2500 − 1 = 2499
Carry out each of the following multiplications using this identity.
a ![]() 48 × 52
48 × 52 ![]() b
b ![]() 47 × 53
47 × 53 ![]() c
c ![]() 31 × 29
31 × 29 ![]() d
d ![]() 201 × 199
201 × 199
The following exercise gives two examples where manoeuvres with the remainder
are possible.
EXERCISE 5
- a
- A computer macro runs for 200 seconds. Express this in minutes and seconds, and hence find how long it will take to run 7 versions of the macro in succession.
- b
- A training company runs a 25-day programme. Express this time in weeks and days, and hence find how many weeks and days six successive programmes will run.
More mental strategies are discussed in the modules listed in the Assumed Knowledge section of this module.
An algorithm works most efficiently if it uses a small number of strategies that apply in all situations; so algorithms do not resort to techniques of mental arithmetic, such as the use of near-doubles, that are efficient for a few cases but useless in the majority of cases. Algorithms must also be robust, in the sense that they must be easy to remember and implement. The benefit of an algorithm is that it can become an automated process that, once mastered, provides an accurate and efficient means to finding a solution.
Addition algorithm
It is essential that students are fluent with the addition of two single-digit numbers before embarking on any formal addition algorithm.
A detailed explanation of the addition algorithm can be found in the module, Addition of Whole Numbers. Depending on where you mark your carry digits, the standard algorithm comes in versions exemplified by
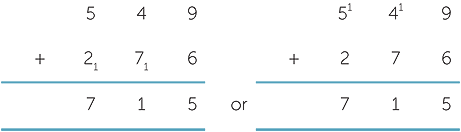
The digits are aligned in columns to ensure that like terms are added. The digits in smaller fonts are the carry. In the standard algorithm, there are different traditions as to where the carry digits and the + symbol are placed.
We can use the standard algorithm to add many numbers together. For example,

Multiplication algorithm
It is essential that students are fluent with addition and with the multiplication
of two single-digit numbers before embarking on any formal multiplication algorithm.
The distributive property is at the heart of our multiplication algorithm. It should be reinforced arithmetically, geometrically and algorithmically.
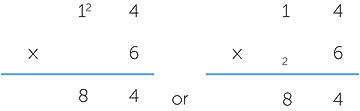
The exact location and size of the carry digit is not essential to the process and varies across cultures. When we do long multiplication, multiple carry digits can arise in each column and recording them in the algorithm can be more of a hindrance than a help. It is therefore desirable to develop a sufficient fluency in multiplying by a single digit so that a student can perform a calculation such as
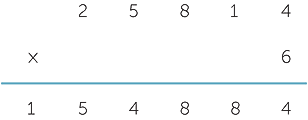
without needing to record the carry digits explicitly. If a student really needs to record the carry digits, then we recommend placing them above the relevant column and crossing them out as they are incorporated into the solution.
We can use the distributive law for long multiplication.
| 74 × 63 | = 74 × (60 + 3) |
| = 74 × 60 + 74 ×3 |
This is used in the two-step calculation below.

This corresponds to the area decomposition below.
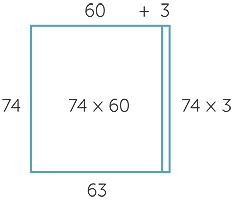
It is not efficient to do this extended long multiplication, but it can be used to highlight the multiple use of distributivity in the process. The area model illustration used in this case reappears later as a geometric interpretation of calculations in algebra.
Subtraction algorithm
Before moving on to subtraction algorithms, students need to be fluent in all subtractions for which the addition table of single-digit numbers provides the complementary additions. For example, both 12 − 4 = 8 and 12 − 8 = 4 have the complementary addition 12 = 8 + 4.

We encourage fluency with addition and subtraction involving whole numbers up to and including 20 (instead of 18 as is done in the addition table) because it is useful to learn and because fluency aids calculations.
There are two common algorithms for subtraction.
The equal addition method (also known as ‘borrow and pay back’)
This method is based on the observation that adding 10 to both numbers does not change the difference between them. So we write
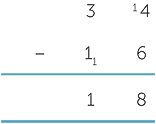
to mean that we add ten ones to 34 and one ten to 16. The algorithm works because, arithmetically, we are actually subtracting 26 from 44. The difference between 44 and 26 is the same as the difference between 34 and 16. This is shown in the following illustration of the number line.

In the subtraction below, we are adding ‘ten tens’ to the top line and adding one hundred to the bottom line.

If there are many zeroes, we may need to perform equal addition in several columns before we can complete the calculation, as illustrated below.

The traditional terminology for equal addition, “borrow and pay back”, is an unfortunate term because it does not accurately describe the process. The phrase “add the same to both numbers” is a more accurate description of the equal addition principle.
The decomposition method (also known as ‘trading’)
The names trading and decomposition come from the place-value representation of the numbers, as modelled by Diene’s blocks (MAB). The subtraction of one from the tens column and addition of ten to the ones column can be viewed as the “long” block being traded for, or decomposed into, ten “ones”.
We calculate 34 − 16 by writing 34 as 20 + 14 instead of 30 + 4.
| 34 − 16 | = (20 + 14) − (10 + 6) | |
| = (20 − 10) + (14 − 6) | ||
| = 10 + 8 |
Algorithmically, we indicate the new regrouping as a conversion of one ten into ten ones.

Consider the following calculation.

This can get messy using the decomposition method if you don’t have a good number sense. We could implement the calculation one column at a time, but this is time consuming and can get untidy and hard to follow. It is sometimes referred to as cascading trades. For example,
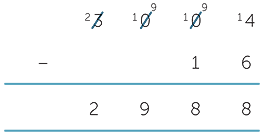
A student might say ‘I haven’t got any tens’. The key is to think of the 3000 as 300 tens and shift one of the tens over to the ones column, leaving you with 299 tens.
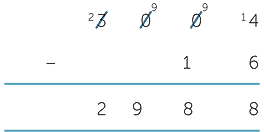
This way the calculation looks clean, is fast and is easy to check.
EXERCISE 6
Calculate 20 300 − 18 782 using equal addition and using decomposition to compare the two techniques.
The advantages and disadvantages of the equal addition and decomposition algorithms
An advantage of the equal addition method is that it is easier to use and produces a tidier and less cluttered layout. A disadvantage of the method is that the mathematics underpinning the technique has an extra layer of complexity.
An advantage of the decomposition method is that it is initially easier to explain, especially using place-value blocks. The algorithm depends on expressing one number in a more convenient format. A disadvantage is that the layout can get messy, mainly because of all of the markings, and this can lead to more errors.
Division algorithm
There is only one standard division algorithm, despite its different appearances. The algorithm can be set out as a ‘long division’ calculation to show all the steps, or as a ‘short division’ algorithm where only the carries are shown, or with no written working at all.
We develop the algorithm using the example 2193 ÷ 5 .
We need to locate 2193 between multiples of 5. To do this, we locate 2193 successively between multiples of 500, multiples of 50 and multiples of 5, subtracting each time to see how much further we have to go.
- Locate 2193 between 2000 = 5 × 400 and 2500 = 5 × 500.
Then subtract 2000 to give 2193 − 2000 = 193.
Thus 2193 = 5 × 400 + 193. - Locate 193 between 150 = 5 × 30 and 200 = 5 × 40.
Then subtract 150 to give 193 − 150 = 43.
Thus 2193 = 5 × 400 + 5 × 30 + 43. - Locate 43 between 40 = 5 × 8 and 45 = 5 × 9.
Then subtract 40 to give 43 − 40 = 3. Thus
2193 = 5 × 400 + 5 × 30 + 5 × 8 + 3.
Putting all this together,
![]() 2193 = 5 × 438 + 3
2193 = 5 × 438 + 3 ![]() and
and ![]() so 2193 ÷ 5 = 438 remainder 3.
so 2193 ÷ 5 = 438 remainder 3.
The calculations above used place value so that at each step, we only needed to know the first nine multiples of 5.
Setting a calculation out as a long division
We could set the work out as follows:
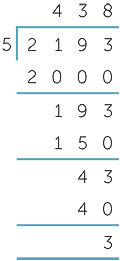 5 × 400 = 2000, then subtract 2000 from 2193
5 × 400 = 2000, then subtract 2000 from 2193
5 × 30 = 150, then subtract 150 from 193
5 × 8 = 40, then subtract 40 from 43
The standard ‘long division’ setting-out, however, allows place value to work for us even more efficiently, by working only with the digits that are required for each particular division. At each step another digit is required — this is usually called ‘bringing down the next digit’.
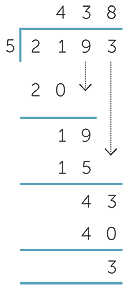 Divide 21 by 5.
Divide 21 by 5.
5 × 4 = 20, then subtract 20 form 21.
Bring down the 9, and divide 19 by 5.
5 × 3 = 15, then subtract 15 from 19.
Bring down the 3, and divide 43 by 5.
5 × 8 = 40, then subtract 40 from 43.
Hence 2193 ÷ 5 = 138 remainder 3.
Hence 2193 ÷ 5 = 438 remainder 3. (Always gather the calculation up into a conclusion.)
The placing of the digits in the top line is crucial. The first step is ‘5 into 21 goes 4’, and the digit 4 is placed above the digit 1 in 21.
Setting a calculation out as a short division
Once the steps have been mastered, many people are comfortable doing each multiplication− subtraction step mentally and writing down only the carry. The calculation then looks like this:
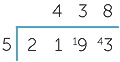 We say, ‘5 into 21 goes 4, remainder 1’.
We say, ‘5 into 21 goes 4, remainder 1’.
‘5 into 19 goes 3, remainder 4’.
‘5 into 43 goes 8, remainder 3’.
EXERCISE 7
Solve each problem first using long division setting-out, then using short division setting-out.
a![]() Express 42 897 days as weeks and days.
Express 42 897 days as weeks and days.
b![]() Express 11 447 months as years and months.
Express 11 447 months as years and months.
Zeroes in the dividend
Zeroes will cause no problems provided that all the digits are kept strictly in their correct columns. This same principle is fundamental to all algorithms that rely on place value.
The example to the right shows the long division and short division calculations for
16 070 ÷ 8 = 2008 remainder 6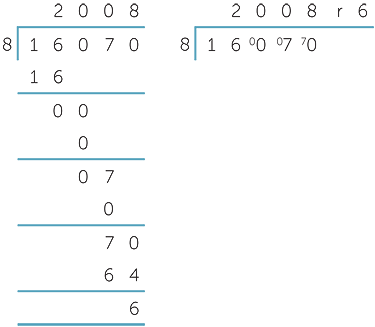
We twice had to bring down the digit 0, and two of the divisions resulted in a quotient of 0.
Long division by numbers with two or more digits
The only extra information we need to implement the division algorithm is the first 9 multiples of the divisor. All of us quickly run out of known multiplication tables, and to divide by any other numbers, begin by writing down the first 9 multiples of the divisor.
Here is the setting-out of the calculations for 13 814 ÷ 17
We begin by writing down the first 10 multiples of 17,
17, 34, 51, 68, 85, 102, 119, 136, 153.
Of course in any given problem we may not need all 9 multiples.
EXAMPLE
Find 97 958 ÷ 123.
Solution
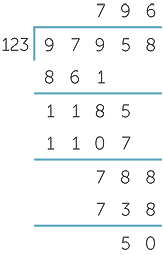 123 × 1 = 123
123 × 1 = 123
123 × 2 = 246
123 × 3 = 369
123 × 4 = 492
123 × 5 = 615
123 × 6 = 738
123 × 7 = 861
123 × 8 = 984
123 × 9 = 1107
That is, 97 958 ÷ 123 = 796 remainder 50.
Note: Once the table is finished, the only arithmetic to be done is subtraction.
EXERCISE 8
- a
- Write down the first 9 multiples of 24, then convert 10 000 hours to days and hours.
- b
- A kilobyte is 210 = 1024 bytes (not 1000 bytes). Write down the first 9 multiples of 1024, then find how many kilobytes and bytes there are in 1 000 000 bytes.
Using the calculator for division with remainder
As with many parts of arithmetic if the numbers are large use a calculator.
EXERCISE 9
- a
- A radar initially pointed north, then rotated clockwise for a few hours. When it was stopped for a calibration check, it registered that it had turned through 53 550o . Use the division button on a calculator to find how many full revolutions it had turned, and its true bearing now.
- b
- Convert 1 000 000 hours to days and hours using the division button on the calculator.
The material in this module lays the foundation for the arithmetic of fractions and decimals. A strong number-sense is an invaluable advantage in life and, essential for further progress in algebra. The understanding of algebra. In particular, the following processes and skills prepare the student for general algebraic manipulations:
- decomposing and recombining numbers
- an understanding of the any-order property of addition and multiplication
- the correct simplification and calculation of expressions involving brackets.
A strong grounding in arithmetic sets a student up for success in algebra.
Applications of arithmetic that are met early include percentages and consumer arithmetic. For example, we calculate the price of an item inclusive of GST by calculating 1.1 times its pre-GST cost and we use arithemetic to calculate discounts. Later in life we calculate mortgage repayments.
These applications are presented in the module, Percentages and the module
Consumer Arithmetic.
A familiarity with multiplication and the expression of numbers as products of factors paves the way for one of the major theorems in mathematics.
The Fundamental Theorem of Arithmetic
Every whole number bigger than 1 can be written as a product of prime numbers and such an expression is unique up to the order in which the factors are written.
The Fundamental Theorem of Arithmetic has far-reaching consequences and applications in computer science, coding, and public-key cryptography. This theorem is discussed in the module, Primes and Prime Factorisation.
The principle of equal addition can be used to reduce subtraction of integers to a two-step problem involving addition and subtraction of whole numbers. For example,
![]() −4 − (−6) = 2 − 0 = 2. (We have added 6 onto both numbers)
−4 − (−6) = 2 − 0 = 2. (We have added 6 onto both numbers)
Classroom activity
Draw a 10 × 10 grid and highlight the multiples of 9 on it. What is the geometric pattern the multiples of 9 make in the table and why does it arise? What is the arithmetic pattern in the digits of the numbers in the 9 times table and why does it arise?
Classroom activity
Draw a 12 × 12 grid with the numbers 1 to 144 written in it. Pick an entry that is not on the edge of the table. How are the numbers immediately above it and immediately below it related to the number in the box you chose? How many things can you say about the numbers to the left and right of the number you chose?
The division algorithm uses multiplication and subtraction. As such, division demands that we synthesise a lot of prior knowledge. This is what makes division challenging, and for many students it is their first taste of multi-layered processes. The ability to reflect on what you know, and implement it within a new, higher-level process is one of the generic mathematical skills that division helps to develop.
The implementation of the division algorithm is typically a multi- step process, and as such it helps to develop skills that are invaluable when students move on to algebra. The link to factors is also critical in later years.
The ability to identify patterns and to engage in open-ended problems are both critical mathematical skills. The multiplication table can be used as a source of activities for both.
Arithmetic itself does not change; 4 + 2 is six regardless of whether you write it as 6 or
VI. Just as the history of number is really all about the development of numerals,
the history of arithmetic is mainly the history of the processes people have used to perform calculations.
The development of the Hindu-Arabic place-value notation enabled the implementation of efficient algorithms for arithmetic and was probably the main reason for the popularity and fast adoption of the notation.
The reader is referred to the history sections of the modules referred to at beginning of this module for further information.
Mathematical Circus, Martin Gardner, Penguin, (1970)
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
Knowing and Teaching Elementary Mathematics: teachers’ understanding of fundamental mathematics in China and the United States. Liping Ma, Mahwah, N.J.: Lawrence Erlbaum Associates, (1999)
EXERCISE 1
100 days is 14 weeks and 2 days.100 ÷ 7 = 14 remainder 2 and 100 = 7 × 14 + 2
EXERCISE 2
- a
- First,we locate 60 between 48 = 24 × 2 and 72 = 24 × 3.
Hence 60 ÷ 24 = 2 remainder 12 or 60 ÷ 24 = 2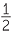 :
:
- i
- 60 hours is 2 days and 12 hours.
- ii
- Each of the 24 periods will be 2
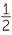 hours.
hours. - b
- First, we locate 2000 between 1920 = 120 × 16 and 2040 = 120 × 17.
Hence 2000 ÷ 120 = 16 remainder 80 or 2000 ÷ 120= 16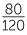 = 16
= 16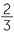 .
. - i
- There will be 16 packets each of 120g, with 80g left over.
- ii
- Each of the 200 packets will contain 16
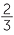 g.
g. - c
- First, we locate 208M between 200M = 20M × 10 and 120M = 20M × 11.
Hence 208M ÷ 20M = 10 remainder 8M or 208M ÷ 20M = 10 = 10.4.
= 10.4. - i
- We can build 10 hospitals, with $8 000 000 left over.
- ii
- Each Australian on average will pay $10.40.
EXERCISE 3
a![]() 248
248![]() b
b![]() 3168
3168![]() c
c![]() 34 034
34 034![]() d
d![]() 816
816
EXERCISE 4
a![]() 2496
2496![]() b
b![]() 2491
2491![]() c
c![]() 899
899![]() d
d![]() 39 999
39 999
EXERCISE 5
a![]() 23 hours 20 minutes
23 hours 20 minutes![]() b
b![]() 21 weeks and 3 days
21 weeks and 3 days
EXERCISE 6
1518
EXERCISE 7
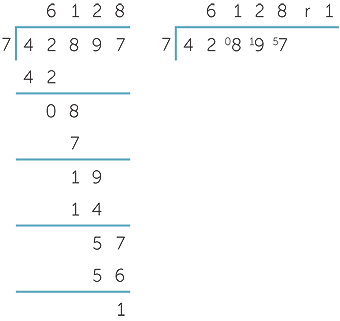 |
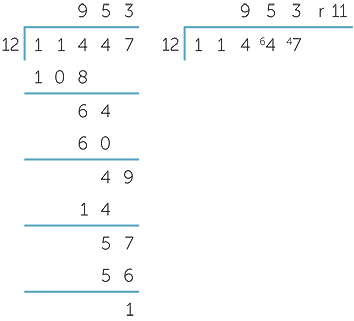 |
|
| Hence 42 897 days is 6128 weeks and 1 day. | Hence 11 445 months is 953 years and 11 months |
EXERCISE 8
a![]() 24, 48, 72, 96, 120, 144, 168, 192, 216, 240
24, 48, 72, 96, 120, 144, 168, 192, 216, 240
![]()
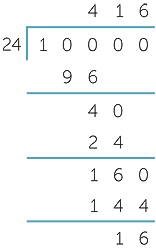
![]() Hence 1 000 000 hours is 416 days and 10 hours.
Hence 1 000 000 hours is 416 days and 10 hours.
b![]() 1024, 2048, 3072, 4096, 5120, 6144, 7168, 8192, 9216, 10 240
1024, 2048, 3072, 4096, 5120, 6144, 7168, 8192, 9216, 10 240
![]()
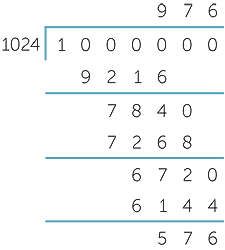
![]() Hence 1 000 000 btyes is not 1000 kilobytes, but is 976 kilobytes and 576 kilobytes.
Hence 1 000 000 btyes is not 1000 kilobytes, but is 976 kilobytes and 576 kilobytes.
EXERCISE 9
- a
- Using the division button, 53 550 = 148
 = 148
= 148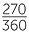 ; so 53 550 = 148 revolutions
; so 53 550 = 148 revolutions
and 270°. So it had turned 345 full revolutions, and was now pointing west. - b
- Using the division button, 1 000 000 ÷ 24 = 41 666 : 666 666… = 41 666
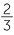 .
.
Hence 1 000 000 hours is 41 666 days and 16 hours.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


