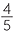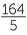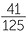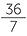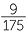The Improving Mathematics Education in Schools (TIMES) Project
- Fluency with addition, subtraction, multiplication and division of whole numbers and fractions.
- Some experience with percentages and decimals.
Percentages are a way of writing numbers with denominator 100. For example,
![]()
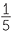 =
=  = 20%,
= 20%, 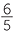 =
= 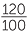 = 120% and
= 120% and  =
= 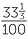 = 33
= 33 %.
%.
Percentages are used widely and in many different areas. For example, discounts in shops, bank interest rates, rates of inflation and many statistics in the media are expressed as percentages. Percentages are important for understanding the financial aspects of everyday life.
Much of what we buy in the shops has a 10% Goods and Services Tax (GST) included in the price. The GST is a tax of one dollar for each ten dollars in the price of the item.
Percentages are a useful way of comparing fractions with different denominators. Percentages give information which is often easier to understand than fractions. For example a statement such as ‘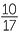 of a popluation have brown hair’ is quite difficult to interpret, while the statement ‘60% of a population have brown hair’ is easier to understand (
of a popluation have brown hair’ is quite difficult to interpret, while the statement ‘60% of a population have brown hair’ is easier to understand (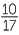 ≈ 59%).
≈ 59%).
The symbol for percent is % and its similarity to /100 reminds us of its meaning. Percentage is another way to write fractions with a denominator of 100. For example, 8% means  .
.
Thus, ![]() 25% =
25% = 
![]() 99% =
99% = 
![]() 150% =
150% = 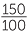 .
.
To understand percentages, we need only remember that percent means ‘out of one hundred’.
A square that has been cut into 100 smaller squares can be used to model percentages.
 If we colour any three of them, we say that ‘3 out of a hundred’ or ‘3 percent’ are coloured in.
If we colour any three of them, we say that ‘3 out of a hundred’ or ‘3 percent’ are coloured in.
We can write  = 3%.
= 3%.
 If we colour 50 of them, we say that ‘50 out of a hundred’ or ‘50 percent’ are coloured in.
If we colour 50 of them, we say that ‘50 out of a hundred’ or ‘50 percent’ are coloured in.
We can write  = 50%. This is equivalent to
= 50%. This is equivalent to 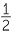 .
.
Writing percentages as fractions and decimals
Percentages are fractions with a denominator of 100. To convert a percentage to its fraction equivalent, we begin by writing it with a denominator of 100. We can then simplify.
When the number is a whole number we just need to write it as fraction and simplify.
For example,
![]() 65% =
65% =  =
= 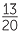
![]() 150% =
150% = 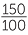 = 1
= 1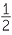 .
.
We can write these percentages as decimals by writing them as fractions with a denominator of 100 and converting to a decimal. For example,
![]() 65% =
65% =  = 0.65
= 0.65 ![]() 150% =
150% = 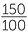 = 1.5.
= 1.5.
When we are not dealing with percentages where the number is not a whole number we need to calculate an ‘equivalent fraction’.
For example, 45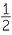 % =
% = 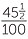 =
= 
To write a percentage as a decimal, we divide by 100. For example,
![]() 62.5% =
62.5% = 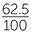 = 0.625
= 0.625
EXAMPLE
Write each percentage as a fraction
a 32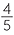 %
% ![]() b 5
b 5 %
%
Solution
|
a 32 |
b 5 |
EXERCISE 1
Write each percentage as a fraction
a![]() 98%
98% ![]() b
b![]() 56
56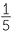 %
%
Writing fractions and decimals as percentages
Fractions with a denominator of 100 are easily written as percentages.
For example,
![]()
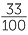 = 33%
= 33% ![]()
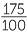 = 175%.
= 175%.
To write a fraction as a percentage, first see if it is possible to find an equivalent fraction with denominator of 100.
For example,
![]()
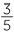 =
=  = 60%
= 60% ![]()
 =
= 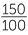 = 150%.
= 150%.
When a fraction does not have an equivalent fraction with a denominator of 100,
multiply the fraction by 100%. This does not change the fraction as 100% =  = 1.
= 1.
For example,  =
=  × 100% = 16
× 100% = 16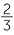 %.
%.
EXAMPLE
Write 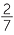 as a percentage.
as a percentage.
Solution
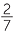 × 100% =
× 100% = 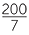 % = 28
% = 28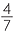 %
%
EXERCISE 2
Write each of the following as percentage:
a 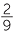
![]() b
b 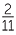
![]() c
c 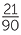
![]() d
d 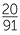
Similarly, to write a decimal as a percentage multiply by 100%.
![]() 0.6 = 0.6 × 100% = 60%
0.6 = 0.6 × 100% = 60%
![]() 3.2 = 3.2 × 100% = 320%
3.2 = 3.2 × 100% = 320%
Here are some commonly used percentages and their fraction equivalents.
It can be quite useful for students to know the following:
| 0 = 0% | 1 = 100% |
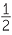 = 50% = 50%
|
 = 25% = 25%
|
 = 75% = 75%
|
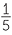 = 20% = 20%
|
 = 40% = 40%
|
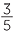 = 60% = 60%
|
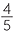 = 80% = 80%
|
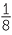 = 12.5% = 12.5%
|
 = 37.5% = 37.5%
|
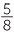 = 62.5% = 62.5%
|
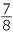 = 87.5% = 87.5%
|
 = 33 = 33 % %
|
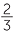 = 66 = 66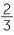 % %
|
|
Expressing one quantity as a percentage of another
Sometimes we want to describe one quantity as a percentage of another.
EXAMPLE
There are 50 people in a swimming club, and 35 go to squad training on one occassion. Calculate the number of people who go to squad training as a percentage of the number of swimming club members.
Solution
35 of the 50 go to squad training.
Percentage in squad = 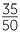 × 100%
× 100%
![]() =
= 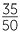 ×
× 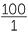 %
%
![]() = 70%
= 70%
So, 70% of the swimming club members go to squad training.
EXAMPLE
Express 55 as a percentage of 120.
Solution
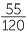 × 100% =
× 100% =  %
%
![]() = 45
= 45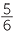 %
%
Therefore 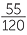 = 45
= 45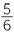 %
%
We often use percentages in the following way.
EXAMPLE
25% of people in a city watched the tennis grand final. Calculate how many people watched the tennis grand final if
The population of the city is 3 000 000
Solution
Number of people watching = 25% of 3 000 000
![]() =
=  ×
× 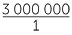
![]() = 750 000
= 750 000
The unitary method has been discussed in the module, The Unitary Method.
Many percentage calculations can be carried out using this method.
The most common units used are 10% = 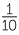 or 1% =
or 1% =  .
.
EXAMPLE
Find ![]() a 70% of 3000
a 70% of 3000 ![]() b 7% of 3000
b 7% of 3000
Solution
a ![]() 100% of 3000 is 3000
100% of 3000 is 3000
![]()

![]() 10% of 3000 is 300
10% of 3000 is 300
![]()

![]() 70% of 3000 is 2100
70% of 3000 is 2100
b ![]() 100% of 3000 is 3000
100% of 3000 is 3000
![]()

![]() 1% of 3000 = 30
1% of 3000 = 30
![]()

![]() 7% of 3000 = 210
7% of 3000 = 210
EXERCISE 3
a ![]() Use the unitary method to find 30% of $14 000
Use the unitary method to find 30% of $14 000
b ![]() Use the unitary method to find 45% of $52 000
Use the unitary method to find 45% of $52 000
Percentages are often used to compare ratios (fractions) by expressing them as percentages. For example in two tests a student receives 72 out of 85 and 37 out 45. Expressing these results as percentages gives 84.7% and 82.2%, where the percentages
are given correct to one decimal place. Hence the first result is better.
EXAMPLE
Two bakeries called Browie and Best Bake both bake bread. On a particular day, 27 out of 40 loaves in Browie Bakery were baked on the previous day. At the Best Bake Bakery 57 out of 90 loaves were baked the previous day. Which bakery was selling the larger percentage of loaves baked the previous day?
Solution
The percentage of loaves baked on the previous day for the Browie Bakery is:
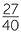 × 100% =
× 100% =  %
%
![]() =
= 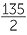 %
%
![]() = 67
= 67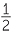 %
%
The percentage of loaves baked on the previous day for the Best Bake Bakery is:
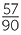 × 100% =
× 100% =  %
%
![]() =
= 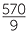 %
%
![]() = 63
= 63 %
%
The Browie Bakery had the greater percentage of loaves baked a day earlier.
EXERCISE 4
A student scores 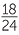 in one test and
in one test and 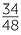 in a second test. Express each score as a percentage and hence state the better score.
in a second test. Express each score as a percentage and hence state the better score.
The unitary method can be used to find 100% of an amount given a percentage of that amount. For example, if 10% of an amount of money is $23, then 100% is 10 × $23 = $230.
EXAMPLE
8% of an amount of money is $6000. What is the amount of money?
Solution
8% of the amount is $6000

![]() 1% of the amount is $750
1% of the amount is $750

![]() 100 % of the amount is $75 000
100 % of the amount is $75 000
The amount of money is $75 000
EXAMPLE
A population of ants increases by 20% in a week and the new population is 125 508.
What was the population at the beginning of the week?
Solution
120% of the original population is 125 508

![]() 20% of the original population is 20 918
20% of the original population is 20 918

![]() 100% of the original population is 104 590
100% of the original population is 104 590
The population at the beginning of the week was 104 590
EXERCISE 5
In the following use the unitary method.
a ![]() Forty percent of an amount of money is $56 000. Find the amount of money.
Forty percent of an amount of money is $56 000. Find the amount of money.
b ![]() Julie receives $3600 in interest from a term deposit for a year which pays
Julie receives $3600 in interest from a term deposit for a year which pays ![]() 6% per annum. How much did Julie invest?
6% per annum. How much did Julie invest?
Sums and differences of percentages
Percentages can sometimes be added and subtracted. In practical applications it is important that you are adding or subtracting percentages of the same quantity.
EXAMPLE
60% percent of people on a large railway platform are reading a newspaper and
24% are reading a novel. The other people on the platform are not reading.
What is the percentage of people on the platform who are
a ![]() reading?
reading? ![]() b
b![]() not reading?
not reading?
Solution
a ![]() Percentage of people reading = 60% + 24% = 84%
Percentage of people reading = 60% + 24% = 84%
![]() 84% of people on the platform are reading
84% of people on the platform are reading
b ![]() Percentage of people not reading = 100% − 84% = 16%
Percentage of people not reading = 100% − 84% = 16%
![]() 16% of people on the platform are not reading
16% of people on the platform are not reading
In the module, Sets and Venn Diagrams examples such as 60% of people on a beach are reading and 70% of the people on the beach are wearing sun glasses and 20% are neither reading nor wearing sunglasses. What is the percentage of people both reading and wearing sun glasses?’
EXERCISE 6
Eighty percent of people in a bus are reading a newspaper. Fifteen percent are reading a novel. A person cannot be reading both.
a ![]() What is the percentage of the people in the bus who are either reading a newspaper
What is the percentage of the people in the bus who are either reading a newspaper ![]() or a novel?
or a novel?
b ![]() What is the percentage of the people in the bus who are neither reading a newspaper
What is the percentage of the people in the bus who are neither reading a newspaper ![]() nor a novel?
nor a novel?
Multiplication of percentages arises from situations such as 55 % of class are boys and 30% of them have blue eyes. The percentage of students in the class who are boys with blue eyes is given by
30% of 55% =  ×
× 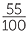 = 16.5%
= 16.5%
EXAMPLE
There are 65 000 spectators in a football stadium. 56% of the spectators barrack for the Reds. 80% of the Reds fans are male.
a ![]() Find the percentage of spectators who are male Reds supporters?
Find the percentage of spectators who are male Reds supporters?
b![]() Find the number of male Reds spectators in the stadium.
Find the number of male Reds spectators in the stadium.
Solution
a ![]() The percentage of spectators who are male Reds supporters = 80% of 56%
The percentage of spectators who are male Reds supporters = 80% of 56%
![]() =
=  ×
× 
![]() =
= 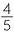 ×
× 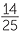
![]() =
= 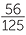
The fraction can be converted to a percentage by multiplying by 100%
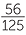 =
= 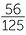 × 100%
× 100%
![]() =
= 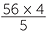 %
%
![]() = 44. 8%
= 44. 8%
b ![]() 44. 8% of 65 000 =
44. 8% of 65 000 = 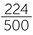 × 65 000
× 65 000
![]() = 29 120
= 29 120
EXERCISE 7
Sixty percent of a group of people work full time. Fifteen percent of those who work full time are married. What is the percentage of people of the group who are married and work full time.
Percentage increase and decrease
Percentage increase and decrease are discussed in the module, Consumer Arithmetic.
Percentages are not only used to express change but also give us the ability
to compare change.
EXAMPLE
An island has two types of rats on it.
On January 1st 2005 there were 670 Creepy rats and on January 1st 2006 the number of these rats had increased to 1260.
On January 1st 2005 there were 230 Slinky rats and on January 1st 2006 the number of these rats had increased to 659.
Find the percentage increase of the number of each type of rat.
Solution
Creepy rats increase by 1260 − 670 = 590
Percentage increase =  × 100%
× 100%
![]() =
= 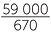 %
%
![]() = 88
= 88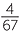 %
%
![]() ≈ 88.06%
≈ 88.06%
Slinky rats increase by 659 − 230 = 429
Percentage increase =  × 100%
× 100%
![]() = 186
= 186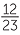 %
%
![]() ≈ 186.52%
≈ 186.52%
EXERCISE 8
City A has a population of 989 000 on January 1 2006 and a population of 1 078 000 on January 1 2008.
City B has a population of 456 000 on January 1 2006 and a population of 501 000 on January 1 2008.
Find the percentage change for each of the cities and hence state which city has the fasting growing population for the period.
The discussion of percentages continues in the module, Consumer Arithmetic and also the module, Rates and Ratios.
Long before decimals were used the need to work with tenths, twentieths and hundredths was evident. Roman taxes were calculated on the basis of these types of fractions. For example Emperor Augustus (63 BC - 19 AD) levied a tax of 1% on goods sold at auction and a tax of 4% on every slave sold. The Romans did not use this notation but certainly employed the concept that we use today.
The concept of percentages has been used since ancient times, but the use of the % sign, is quite recent and its exact history uncertain.
EXERCISE 1
a 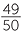
![]() b
b 
EXERCISE 2
a 22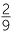 %
% ![]() b 18
b 18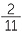 %
% ![]() c 23
c 23 %
% ![]() d 21
d 21 %
%
EXERCISE 3
a $4200 ![]() b $23 400
b $23 400
EXERCISE 4
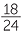 = 75% and
= 75% and 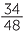 = 70
= 70 %
%
Therefore 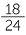 is the higher score.
is the higher score.
EXERCISE 5
a $140 000 ![]() b $600 000
b $600 000
EXERCISE 6
a 95% ![]() b 5%
b 5%
EXERCISE 7
9%
EXERCISE 8
City A: percentage change ≈ 9.0%
City B: percentage change ≈ 9.8%
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()