The Improving Mathematics Education in Schools (TIMES) Project
Multiplication of Whole Numbers
Number and Algebra : Module 9![]() Year : 4-7
Year : 4-7
June 2011
- An understanding of place value as applied to whole numbers (see module on Counting and Place Value).
- An appreciation that addition can be modelled by combining sets of objects, and can also be modelled on a number line.
- An understanding of, and fluency with, skip-counting.
- An understanding of, and fluency with, addition of two single-digit numbers.
- Familiarity with the use of arrays to model multiplication.
- The use of the multiplication symbol to mean “groups of”.
- Knowledge of simple multiplication and division facts.
Examples of the use of multiplication include calculating the cost of six items
costing 25 cents each. It is much quicker to calculate 6 × 25 by multiplication
than by repeated addition.
Multiplication answers questions such as:
1 Judy bought 15 boxes of chocolates. Each box contained 24 chocolates. How many chocolates did Judy have?
2 Henry has 16 rolls of wire. Each roll is 18 m long. What is the total length of wire that Henry has?
The natural geometric model of multiplication as rectangular area leads to applications in measurement. As such, multiplication provides an early link between arithmetic and geometry.
Fluency with multiplication reduces the cognitive stress in learning later topics such
as division. The development of a solid understanding of arithmetic is essential for all further mathematics.
For whole numbers, multiplication is equivalent to repeated addition.
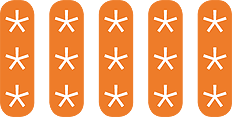
Modelling multiplication by arrays
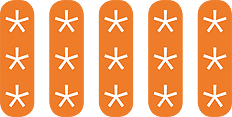
The use of arrays to model multiplication is essential. For example, 3 × 5 is illustrated by

We call 15 the product of 3 and 5, and we call 3 and 5 factors of 15.
By looking at the rows of the array we see that
3 × 5 = 5 + 5 + 5

By looking at the columns of the array we also see that
5 × 3 = 3 + 3 + 3 + 3 + 3
This illustrates 3 × 5 = 5 × 3. We say that multiplication is commutative.
Modelling multiplication by skip-counting
Skip-counting, such as reciting 3, 6, 9, 12, 15,..., is one of the earliest introductions to repeated addition and hence to multiplication. This can be illustrated on a number line as shown for 3 × 5 = 15 below.

3 × 5 = 15
On the number line, the fact that 3 + 3 + 3 + 3 + 3 = 5 + 5 + 5 is not so obvious; the above diagram shows 5 + 5 + 5, whereas 3 + 3 + 3 + 3 + 3 on a number line looks quite different.
Skip-counting is important because it helps children learn their multiplication tables.
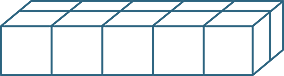
Modelling multiplication by area
Replacing objects in an array by unit or 1 × 1 squares introduces the area model of multiplication. This is illustrated below for 3 × 5.

At this stage, we are using unit squares instead of counters or stars. We can also use the area model of multiplication for multiplication of fractions.
Learning the multiplication table
Fluency with multiplication tables is essential for further mathematics and in everyday life.
If students can add a single-digit number to a two-digit number, they can at least reconstruct the multiplication table even if they have not yet developed fluency. It is therefore essential to ensure that students can add fluently.
We strongly recommend that students learn their multiplication facts up to 12 × 12. This is primarily because the 12 times table is essential for time calculations — there are 12 months in a year, 24 hours in a day, and 60 minutes in an hour. Familiarity with dozens is useful in everyday life because packaging in 3 × 4 arrays is so much more convenient than in 2 × 5 arrays. In addition, the 12 × 12 table has many patterns that can be constructively exploited in pre-algebra exercises.
A straightforward approach to learning the tables is to recite each row, either by heart or by skip-counting. However, students also need to be able to recall individual facts without resorting to the entire table.
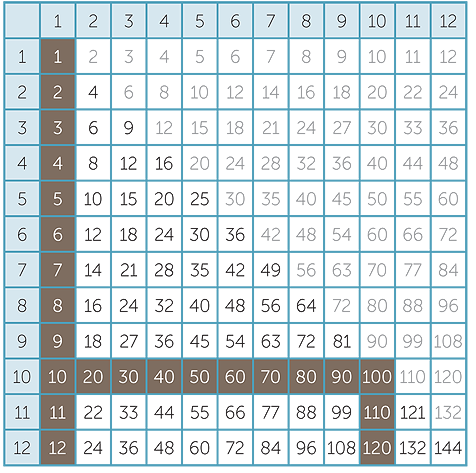
Looking at the 12 × 12 multiplication table gives the impression that there are 144 facts to be learnt.

However, there are several techniques that can be used to reduce the number of facts to be learnt.
- The commutativity of multiplication immediately reduces 144 to 78.
- The 1 and 10 times tables are straightforward and their mastery reduces the number
of facts to be learnt to 55.
- The 2 and 5 times tables are also easy to learn and their mastery further reduces the number of facts to be learnt to 36.
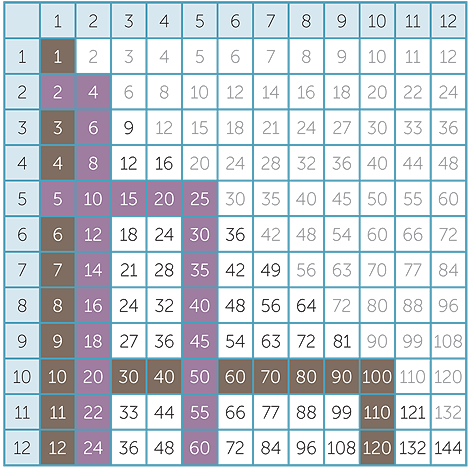
- The 9 and 11 times tables are the next easiest to skip-count because 9 and 11 differ from 10 by 1. This reduces the number of facts to 21.
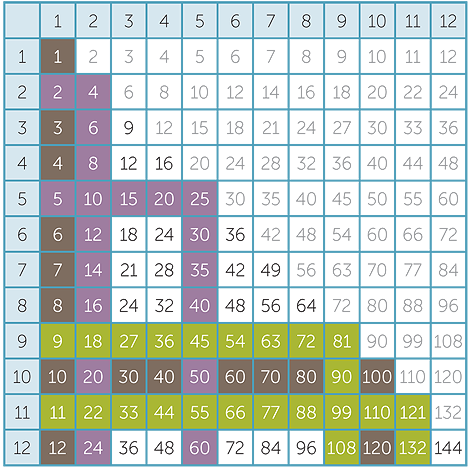
- The squares are useful and can be learnt just as one might learn a times table.
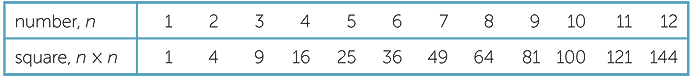
This reduces the number of terms to be learnt to 15.
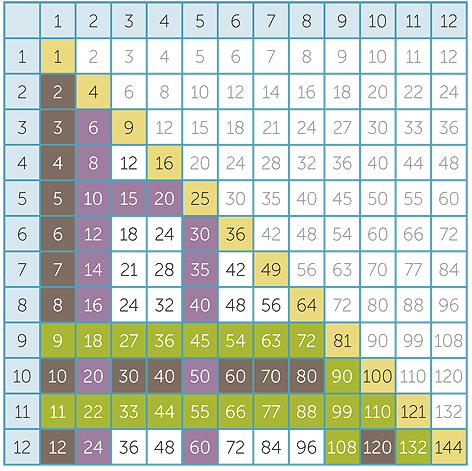
Whatever techniques are used, the aim should be fluency.
Commutativity
One of the advantages of the array and area approach is that properties of multiplication are more apparent.
As discussed above, turning the 3 × 5 array on its side illustrates that 3 × 5 = 5 × 3 because the area does not change.
 |
 |
|
| 3 × 5 = 5 × 3 | ||
We saw this before by looking at the rows and columns separately, but we can also do this by turning the rectangle on its side, that is, by rotation.
 3 × 5 = 5 × 3 3 × 5 = 5 × 3 |
 |
Any-order property
Another important property of multiplication is associativity, which says that
a × (b × c) = (a × b) × c for all numbers.
Associativity of multiplication ensures that the expression a × b × c is unambiguous. We usually don’t teach associativity of multiplication explicitly in years 4 -7. Instead, we teach the any-order property of multiplication, which is a consequence of the commutative and associative properties.
Any-order property of multiplication
A list of numbers can be multiplied together in any order to give the product of the numbers.
The any-order property of multiplication is analogous to the any-order property of addition. Both associativity and commutativity are nontrivial observations; note that subtraction and division are neither commutative nor associative. Once we are familiar with the arithmetic operations we tend to take both associativity and commutativity of multiplication for granted, just as we do for addition. Every so often, it is worth reflecting that commutativity and associativity combine to give the important and powerful any-order properties.
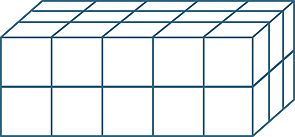
Multiplying three whole numbers corresponds geometrically to calculating the number of unit cubes in (or volume of) a rectangular prism. The any-order property of multiplication means that we can calculate this volume by multiplying the lengths of the sides in any order. The order of the calculation corresponds to slicing the volume up in different ways.
 |
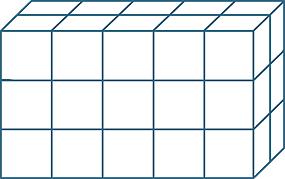 |
|||
| 5 × 2 = 2 × 5 | (5 × 2) × 3 = (2 × 5) × 3 | |||
 |
 |
|||
|
|
|||
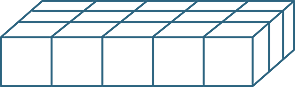 |
 |
|||
| 5 × 3 = 3 × 5 | (5 × 3) × 2 = (3 × 5) × 2 |
Distributivity of Multiplication over Addition and Subtraction.
The equation 3 × (2 + 4) = (3 × 2) + (3 × 4) is an example of the distributivity
of multiplication over addition. With arrays, this corresponds to the
following diagram.
 =
= 
With areas it corresponds to the diagram below.
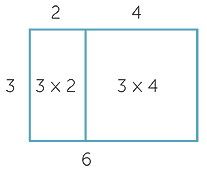 |
Area = 3 × 6 |
Multiplication is also distributive over subtraction.
For example 7 × (10 − 2) = 7 × 10 − 7 × 2. This can be illustrated by the area model.
The any-order property of multiplication and the distributive law for multiplication allow some multiplication problems to be completed without complicated calculations.
Using the any-order property
We use the any-order property of multiplication to simplify calculations by changing
the order in which we perform multiplications. For example,
| 1 |
|
||
|
|||
| 2 | 2 × 17 × 5 = 10 × 17 | ||
| 3 | 25 × 7 × 4 = 25 × 4 × 7 = 100 × 7. |
Sometimes this reordering happens after we decompose one of the factors,
such as when we double twice in order to multiply by four, as in
17 × 4 = (17 × 2) × 2 = 34 × 2 = 68.
This technique of moving a factor from one number to another in order
to simplify a calculation has applications beyond repeated doubling, as in
36 × 5 = 18 × (2 × 5) = 180.
This is sometimes called “halve and double“.
EXERCISE 1
Use the any-order property to carry out the following multiplications.
| a | 5 × 7 × 2 | b | 68 × 5 | c | 25 × 11 × 4 |
Using the distributive property
We use both distributive properties to simplify some multiplication problems. For example,
7 × 101 = 7 × (100 + 1) = 700 + 7 = 707,
7 × 99 = 7 × (100 − 1) = 700 − 7 = 693,
7 × 102 = 7 × (100 + 2) = 700 + 14 = 714,
and
7 × 98 = 7 × (100 − 2) = 700 − 14 = 686.
Some examples of this nature can be used to develop concepts needed in the formal algorithm. Observations such as 14 × 60 = 14 × 6 × 10 and 14 × 600 = 14 × 6 × 100 are fundamental to the understanding of the multiplication algorithm.
Calculations such as
21 × 7 = 20 × 7 + 1 × 7 = 140 + 7 = 147
can be done first as a mental strategy, and then used as early examples in the formal algorithm. Other mental strategies related to the algorithm include observations such as
200 × 81 = 2 × 81 × 100 = 162 × 100 = 16 200
where multiplying by single-digit multiples of powers of ten is really no more complicated than multiplying by the single digit and keeping track of place value.
EXERCISE 2
Use the distributive law to carry out the following multiplications.
| a | 31 × 8 | b | 99 × 32 | c | 1001 × 34 | d | 102 × 8 |
EXERCISE 3
The identity (a − b)(a + b) = a2 − b2 is also useful for mental computation.
For example: 49 × 51 = (50 − 1) × (50 + 1) = 2500 − 1 = 2499
Carry out each of the following multiplications using this identity.
| a | 48 × 52 | b | 47 × 53 | c | 31 × 29 | d | 201 × 199 |
An algorithm works most efficiently if it uses a small number of steps that apply in
all situations. So algorithms do not resort to techniques, such as the use of near-doubles, that are efficient for a few cases but useless in the majority of cases.
The standard algorithm will not help you to multiply two single-digit numbers. It is essential that students are fluent with the multiplication of two single-digit numbers before embarking on any formal algorithm.
Standard Algorithms
The distributive property is at the heart of our multiplication algorithm because it enables us to calculate products one column at a time and then add the results together. It should be reinforced arithmetically, geometrically and algorithmically. For example, arithmetically we have 6 × 14 = 6 × 10 + 6 × 4, geometrically we see the same phenomenon,
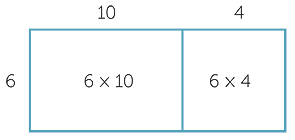
and algorithmically we implement this in the following calculation.
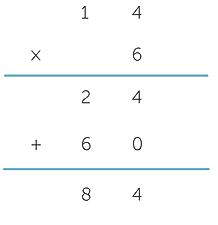
Once this process and layout is understood, we can proceed to the contracted algorithm.
Multiplying by a single digit
First we contract the calculation by keeping track of carry digits and incorporating the addition as we go. The previous calculation shortens as either

depending on where the carry digits are recorded.
Care should be taken even at this early stage because of the mixture of multiplication and addition. Note also that the exact location and size of the carry digit is not essential to the process and varies across cultures. When we do long multiplication, multiple carry digits can arise in each column and recording them in the layout can be more of a hindrance than a help. It is therefore desirable to develop a sufficient fluency in multiplying by a single digit so that a student can perform a calculation such as
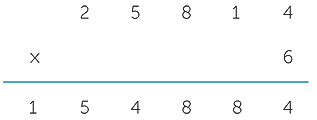
without needing to record the carry digits explicitly. If a student really needs to record the carry digits, then we recommend placing them above the relevant column and crossing them out as they are incorporated into the solution.
Multiplying by a single digit multiple of a power of ten
The next observation is that multiplying by a single-digit multiple of ten is no harder than multiplying by a single digit provided we keep track of place value. So, to find the number of seconds in 14 minutes we calculate
14 × 60 = 14 × 6 × 10 = 840
and implement it in a layout such as
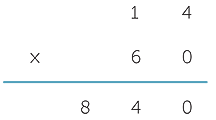
Similarly, we can keep track of higher powers of ten by using place value to our advantage. So
14 × 600 = 14 × 6 × 100 = 8400
becomes
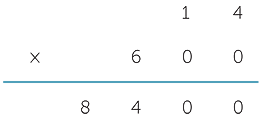
For students who have met the underlying observation as part of their mental arithmetic exercises the only novelty at this point is how to layout these calculations.
Multiplying by a two-digit number
The next cognitive jump happens when we use distributivity to multiply two two-digit numbers together. This is implemented as two products of the types mentioned above. For example,
74 × 63 = 74 × (60 + 3) = 74 × 60 + 74 × 3
is used in the two-step calculation below.

This corresponds to the area decomposition illustrated below.
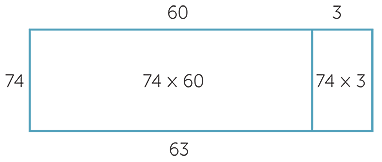
In the early stages, it is worth concurrently developing the arithmetic, geometric and algorithmic perspectives illustrated above.
Unpacking each line in a long multiplication calculation using distributivity explicitly,
as in

This is 74 × 63 = (70 + 4)(60 + 3)
This also corresponds to the area decomposition
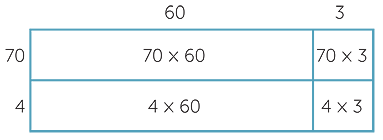
It is not efficient to do this extended long multiplication, but it can be used to highlight the multiple use of distributivity in the process. The area model illustration used in this case reappears later as a geometric interpretation of calculations in algebra.
Multiplying multiple-digit numbers
The more digits in the numbers we are multiplying, the more times we need to apply the distributive property, and the more lines our calculation will have, as shown below.

This example corresponds to: 5974 × 3 + 5974 × 60 + 5974 × 200 + 5974 × 1000
Beyond that, multiplication of whole numbers never really gets any more complicated.
The first application of multiplication that students are likely to meet is division. When calculating a division, we are constantly calculating multiples of the divisor, and lack of fluency with multiplication is a significant handicap in this process. The material in this module lays the foundation for multiplication, and then division, of fractions and decimals.
Other applications of multiplication that are met early include percentages and consumer arithmetic. For example, we calculate the price of an item inclusive of GST by calculating 1.1 times its pre-GST cost.
A familiarity with multiplication and the expression of numbers as products of factors paves the way for one of the major theorems in mathematics.
The Fundamental Theorem of Arithmetic: Every whole number bigger than 1 can be written as a product of prime numbers and such an expression is unique up to the order in which the factors are written. For example, 24 = 23 × 3 and 20 = 22 × 5.
The Fundamental Theorem of Arithmetic has far-reaching consequences and applications in computer science, coding, and public-key cryptography.
Last, but not least, a strong grounding in arithmetic sets a student up for success in algebra.
Using the multiplication table as a source of patterns
The ability to identify patterns and to engage in open-ended problems are both critical mathematical skills. The multiplication table can be used as a source of activities for both.
Classroom activity
Draw a 10 × 10 grid and highlight the multiples of 9 on it. What is the geometric pattern the multiples of 9 make in the table and why does it arise? What is the arithmetic pattern in the digits of the numbers in the 9 times table and why does it arise?
Classroom activity
Draw a 12 × 12 grid with the numbers 1 to 144 written on it. Pick an entry that is not on the edge of the table. How are the numbers immediately above it and immediately below it related to the number in the box you chose? How many things can you say about the numbers to the left and right of the number you chose?
The product of two numbers is the same no matter how you calculate it or how you write your answer. Just as the history of number is really all about the development of numerals, the history of multiplication is mainly the history of the processes people have used to perform calculations. The development of the Hindu-Arabic place-value notation enabled the implementation of efficient algorithms for arithmetic and was probably the main reason for the popularity and fast adoption of the notation.
One technique that is quite different to the standard algorithm is Egyptian Duplation and dates from before 1850 BC. It reduces calculations to a succession of doublings together with a final addition.
Suppose you want to multiply 63 by 22. First write
| 1 | 63 |
then double both numbers and write them below to get
| 1 | 63 | |||
| 2 | 126 |
Continue doubling until the number in the left-hand column is as big as it can be without being bigger than 22. So we write
| 1 | 63 | |||
| 2 | 126 | |||
| 4 | 252 | |||
| 8 | 504 | |||
| 16 | 1008 |
and stop because 32 is bigger than 22.
Now we work our way backwards and start by marking the 16; traditionally this was done by placing a line to the left of the number, as illustrated below.
Adding 8 to 16 gives a number bigger than 22, so we don’t mark the row above.
Since 16 + 4 ≤ 22 we mark the row with 4 in the left-hand column.
Since 16 + 4 + 2 = 22 we mark the row with 2 in the left-hand column,
and since 16 + 4 + 2 + 1 > 22 we do not mark the top row. This leaves us with
| 1 | 63 | |||
| / | 2 | 126 | ||
| / | 4 | 252 | ||
| 8 | 504 | |||
| / | 16 | 1008 |
Adding the numbers in the right column of the marked rows gives
1008 + 252 + 126 = 1386,
which is the product 22 × 63. This works because
22 × 63 = (16 + 4 + 2) × 63 = 1008 + 252 + 126 = 1386.
Egyptian duplation relies on distributivity and the fact that every number can be written as a sum of powers of 2.
EXERCISE 4
Complete the following using Egyptian duplation.
| a | 34 × 56 | b 57 × 34 |
Like Egyptian Duplation, the Russian Peasant Method works because every number has a unique expression in base 2. The Russian Peasant Method reduces calculations to a succession of doublings and halvings together with a final addition.
As an algorithm, Russian Peasant Method works as follows.
- Put the two numbers you want to multiply at the top of two columns.
- Produce another row of two numbers by doubling the number in the first column
and halving the number in the second column, ignoring any remainders in the
halving process. - Repeat the previous step until the number in the halving column is 1.
- Cross out all rows in which the number in the halving column is even.
- Add all the numbers in the doubling column that have not been crossed out.
- This sum is equal to the product of the original two numbers. For example, in using it to calculate 63 × 22 we write
| 126 | 11 | |
| 252 | 5 | |
| 1008 | 1 |
then calculate 126 + 252 + 1008 = 1386 and conclude that 63 × 22 = 1386.
This procedure always works, but why?
Suppose we want to multiply 63 by 16. We begin by writing 63 and 16 at the top of
two columns and below each we write the numbers we get by doubling one and
halving the other.
| 1008 | 1 |
In this case, the product of the two numbers in each row is identical to the product of the numbers immediately above. For example, 126 × 8 = 63 × 16. By following the chain of products we conclude that 63 × 16 = 1008 × 1 = 1008. This works particularly easily because 16 is a power of 2.
Suppose instead we want to multiply 63 by 14.
| 126 | 7 | |
| 252 | 3 | |
| 504 | 1 |
Since there are no remainders in the first division, 126 × 7 = 63 × 14 and the first step has been simply to restate the product in a different way. We can safely cross out 63 × 14 and pretend it was never there to start with. However, at the second step we have ignored a remainder and so there is a difference between the two rows; in particular, 126 × 7 = 252 × 3 + 126 × 1. Note that the difference between the product in the two rows is 126, the number in the upper row in the doubling column. Since the remainder on division by 2 can only ever be 0 or 1, at each step we are either restating the problem exactly, or out by one copy of the number in the doubling column. In this calculation, we have ignored one copy of 126 and one copy of 252 before arriving at our expression 504 × 1. So our original product, 63 × 14 must be equal to 504 + 252 + 126.
In general, there may be several rows in which we have no remainder and several rows in which we are ignoring remainders. We cross out those rows for which the division by 2 resulted in an exact restatement of the product in the previous row; this corresponds precisely to the rows that have even numbers in the halving column. The numbers that have not been crossed out in the doubling column correspond to the remainders and their sum is equal to the original product.
Another technique, known as the Italian or lattice method is essentially an implementation of the extended version of the standard algorithm but in a different layout. The method is very old and might have been the one generally adopted if it had not been difficult to print. It appears to have first appeared in India, but soon appeared in works by the Chinese and by the Arabs. From the Arabs it found its way across to Italy and can be found in many Italian manuscripts of the 14th and 15th centuries.
The multiplication 34 × 27 is illustrated here.
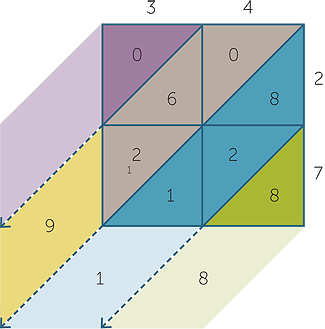
34 × 27 = 918
In the top right rectangle 4 × 2 is calculated. The digit 8 is placed in the bottom triangle and 0 in the top triangle.
Then 3 × 2 is calculated and the result entered as shown.
In the bottom right rectangle 4 × 7 is calculated. The digit 8 is placed in the bottom triangle and the digit 2 in the top triangle. The result of 3 × 7 is also recorded in this way.
The green diagonal contains the units.
The blue diagonal contains the tens.
The brown diagonal contains the hundreds.
The digits are now summed along each diagonal starting from the right and each
result recorded as shown. Note that there is a ‘carry’ from the ‘tens diagonal’ to the ‘hundreds diagonal’
EXERCISE 5
Use the lattice method to carry out each of the following multiplications
| a | 35 × 73 | b | 67 × 87 | c | 453 × 235 |
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
History of Mathematics, D. E. Smith, Dover publications New York, (1958)
https://en.wikipedia.org/wiki/Ancient_Egyptian_multiplication
Exercise 1
| a | 70 | b | 340 | c | 1100 |
EXERCISE 2
| a | 248 | b | 3168 | c | 34 034 | d | 816 |
EXERCISE 3
| a | 2496 | b | 2491 | c | 899 | d | 39 999 |
EXERCISE 4
| a | 1904 | b | 1938 |
EXERCISE 5
| a | 2555 | b | 5829 | c | 106 455 |
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


