The Improving Mathematics Education in Schools (TIMES) Project

return to index

Using place value to write numbers

Number and Algebra : Module 5Years : 4-7

June 2011

PDF Version of module

Assumed Knowledge

• The ability to count up to 1000.
• The ability to write numbers up to 100.
• The ability to add single-digit numbers with accuracy and fluency.

Children learn to count before they learn to write numbers, just as they learn to speak before they learn to write words.

We will make a distinction between a number and a numeral. A number is an abstract concept, whereas a numeral is a symbol used to represent that concept. Thus the number three is the abstract concept common to three chairs, three crayons, and three children, whereas the symbols 3 and III are numerals for the number three.

Motivation

Numeracy and literacy are essential skills in modern society. Just as we need the alphabet to write down words and sentences so we need a notation to write down numbers.

We use a base-ten place-value notation to write numbers. It was developed over several centuries in India and the Arab world, so we call it Hindu-Arabic notation. The place-value nature of Hindu-Arabic notation enabled the development of highly efficient algorithms for arithmetic, and this contributed to its success and wide acceptance.

Hindu-Arabic numerals exhibit some of the qualities that makes mathematics so powerful, namely

• they can be used by understanding a small number of ideas, and
• they can be generalized beyond the original setting for which they were devised.

To illustrate the second point, note that the notation was developed to express whole numbers, but it extends to the representation of fractions and decimals.

A solid understanding of numbers and arithmetic is essential for the development of later concepts including fractions and algebra.

Content

The basics of the system

Hindu-Arabic numerals are a decimal, or base-ten, place-value number system with the ten digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 as fundamental building blocks. Each digit in a number has a place value depending on its position. These positions can be thought of as columns labelled by powers of ten, with the powers increasing from right to left as illustrated in the following table.

When reading Hindu-Arabic numerals, the digit with the largest place value is read first. Thus the number 7352 is read as “seven-thousand, three-hundred and fifty-two”, and we think of it in columns as illustrated in the following table.

These labels are made explicit when we write numbers in expanded form. For example

7352 = 7 × 1000 + 3 × 100 + 5 × 10 + 2

Only one digit is entered in each column.

The digit 0 is essential in the Hindu-Arabic system because it acts as a place-holder.
In the number 302, the 0 tells us that there are ‘no tens’.

Multiplying a number by ten shifts each digit one place to the left. Because there is now nothing in the ones column, we put a 0 in that column as a place holder. The following table illustrates the process for 420 × 10 = 4200.

Dividing by ten shifts the digits one step to the right, and requires decimals unless the last digit in the original number was 0. The following table illustrates this process for
420 ÷ 10 = 3.5

Conventions about spacing and naming

A number with many digits can be hard to read.

Therefore we cluster the digits in groups of three, starting from the ones place,
and separate different groups by a thin space. By convention we do not put a space
in a four-digit number. Thus we write 7352, but 17 352 and 2 417 352.

The nested method that we use to name the columns enables us to read very large numbers using a few basic words such as thousands and millions.

Classroom Activity

Use place-value houses to gather digits into groups of three and to aid in the naming of larger numbers.

So we write the number shown in the place value houses above as 830 427 596 and we say ‘eight hundred and thirty million, four hundred and twenty seven thousand, five hundred and ninety six’. Converting between words and numbers is an important skill.

The following table summarises some column names and their values.

Column value		Name
1	100	one (unit)
10	101	ten
100	102	hundred	ten × ten
1000	103	thousand	ten × hundred
10 000	104	ten thousand
100 000	105	hundred thousand
1 000 000	106	million	thousand × thousand
10 000 000	107	ten million
100 000 000	108	hundred million
1 000 000 000	109	billion	thousand × million
1 000 000 000 000	1012	trillion
	10100	googol

The convention is slightly different when we write about money. It is standard accounting practice to separate the groups of digits by a comma. For example, the average annual salary in Australia was close to $64,200 in 2009. This can cause confusion for two reasons. Firstly, people often see numbers in the context of money and tend to always write large numbers with commas to separate groups of digits. Secondly, the use of a comma is not a world-wide standard. In continental Europe, the groups of digits are separated by points and what we call a decimal point is replaced by a comma. The average annual salary in Spain might be 21.500 euros, but a coffee might only cost 1,20 euros.

The number of numbers

The smallest whole number is zero, written 0.

There is no bound on the number of whole numbers we can express using Hindu-Arabic numerals, although we eventually run out of names.

There are 100 numbers less than 100 including 0.

There are 1000 numbers less than 1000.

There are 10 000 numbers less than 10 000.

There are	10		1-digit numbers.
	90		2-digit numbers.
	900		3-digit numbers.
	9000		4-digit numbers.

Using algorithms

Children’s understanding of place value improves dramatically once they start working with the formal algorithms for addition, subtraction, multiplication and division. These algorithms will be covered in other modules. When using the algorithms there are a number of common errors related to place value.

For example, a common error is to enter two digits into a single column when carrying out the addition algorithm.

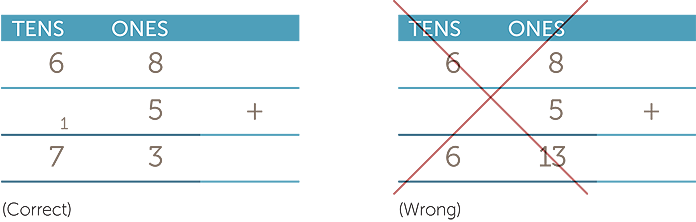
Another common error is forgetting to use 0 as a place marker when performing
long division.

(Correct)		(Wrong)

As we mentioned in the motivation, the existence of fast and efficient algorithms for arithmetic is a major advantage of the Hindu-Arabic numerals.

Other place value number systems

When we work in base ten, the columns represent powers of ten. For example 7352 is shown as

This means 7 × 1000 + 3 × 100 + 5 × 10 + 2.

What happens if we use five instead of ten as the base for the columns? Working in base five the column headings would be powers of five. For example, in base 5, 243 is shown as

This means 2 × 25 + 4 × 5 + 3 × 1 which is 73 in base ten.

Notice that we have to be clear about which base we are working in so as to know
the place value of each digit. We do this by using a subscript to indicate the base,
so we write

243five=73ten.

Converting a number from base ten to another base is a little more complicated and, in the first instance, is best done using hands-on materials.

The following illustrates the conversion of 32ten into a numeral in base five.

Take 32 lollipop sticks and put them into bundles of five.

Thus		= 6 × 5 + 2
		= 5 × 5 + 5 + 2
		= 1 × 25 + 1 × 5 + 2.
So		32ten = 112five

In the base-five system the only the digits are 0, 1, 2, 3 and 4.

Place value systems with bases other than ten are not just curiosities. All computer calculations take place in a base-two, or binary, system and computer scientists often express numbers in hexadecimal, or base-sixteen, notation.

Links Forward

This module has dealt with whole numbers. Once students have mastered whole numbers, we introduce them to integers (the whole numbers together with the negative numbers −1, −2, −3, …) and rational numbers (positive and negative fractions).

The development of the concept of number can be described with the aid of the following diagram.

School mathematics normally follows the historical development of numbers and introduces students first to whole numbers then to positive fractions, then to integers,
and finally to the rational numbers.

History

Note that when we discuss the historical development of this topic we are always
talking about the same numbers. The history of numeration is all about the evolution
of numerals.

Early civilizations developed different ways of writing numbers. Many of these ways were cumbersome and made it hard to do arithmetic.

The most basic and oldest known system of numeration involves tally marks.

The Babylonians

The two earliest civilisations known to have developed writing and written number systems are the Egyptian and Mesopotamian civilisations centred on the modern countries Egypt and Iraq. Mesopotamia probably began to develop as small city-states between 6000 and 7000 years ago.

For various reasons, Mesopotamian mathematics is called Babylonian mathematics and quite a lot is known about it and its users, despite the fact that to date the only clay tablets discovered date from about 1600 BC, 1000 BC and 300 BC.

The Babylonian number system was in base 60 so the number 1, 5, 13 is

1 × 602 + 5 × 60 + 13 = 391310.

This, of course, means that 60 digits from 0 to 59 are needed. In 1600 BC a space was used as a place holder as in 1, 0, 13 but by 300 BC the symbol was used as a zero place holder. The remaining 59 digits were created using a base 10 system. So 34 was drawn as 10, 10, 10, 1, 1, 1, 1 in a neat character grouping.

By 1600 BC the system also represented sexagesimal (base 60) fractions so, depending on the context, 1, 5, 13 could also represent 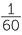+ + 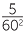. This sexagesimal number system had all the features of the modern decimal place-value system except for the sexagesima point!

The Egyptians

The Egyptians used a system of numeration based on powers of ten, but it was not a place-value system. They used the following hieroglyphs for powers of ten and simply drew as many of each as they needed.

1	10	100	1000	10 000	100 000	106

For example, the number 7352 was written as:

Later, when they started writing on papyrus, they developed a short-hand system based on hieratic numerals illustrated in the table below. Hieratic means “of priests” and reflects the close connection between religion and education at the time.

Hieratic numerals allowed people to write numbers more succinctly and with greater speed than with hieroglyphs.

A brief exposition of the Egyptian number systems can be found at
https://en.wikipedia.org/wiki/Egyptian_numerals

and an interactive hieroglyphic number calculator can be found at
www.eyelid.co.uk/numbers.htm

Roman Numerals

Once civilisations moved from hieroglyphic (picture-based) to alphabet-based writing, letters were used as numerals. The best-known example is the system of Roman numerals, but earlier systems were also developed using the Greek and Hebrew alphabets. We will explain the system of Roman numerals as a general example. The basic numerals are listed in the following table.

Roman numerals are added whenever they were listed in decreasing order, so LXVII represents 50 + 10 + 5 + 1 + 1 = 67. The value of a numeral does not change depending on its location, except in a very local sense. If a numeral is placed immediately to the left of the next-biggest numeral then the smaller numeral is subtracted from the larger; so XI represents 10 + 1 = 11 whereas IX represents 10 − 1 = 9. However, 49 was not be written as IL. Forty nine is written as XI. Since the study of Roman numerals is common in many schools we attach an appendix dealing with the system in greater detail. However, we emphasise that the study of other systems of numeration should not come at the cost of the development of fluency with Hindu-Arabic notation.

Hindu-Arabic notation

The Hindu-Arabic notation was probably developed in India. A place-value system using 9 digits and a space or the word kha (for emptiness) as place marker was used in India the 6th century AD. By the 9th century the system had made its way to the Arab world (including Persia and Al-Andalus in what is now Spain). The digit 0 evolved from “.” and was used in both Madhya Pradesh (Northern India) and the Arab world by the 10th century.

Leonardo of Pisa, known as Fibonacci, learned to use the notation from merchants in Africa when he was a boy. His book, Liber Abaci, in 1202 contained a description of the notation. This book popularized the Hindu-Arabic system in Europe. At about the same time, Maximus Planudes wrote a treatise called The Great Calculation entirely devoted to the Hindu-Arabic notation and the algorithms of arithmetic.

It is no coincidence that the word digit also means the fingers and thumbs on our hands. The fact that we use a base-ten place value system is almost certainly a consequences of a natural tendency to count on our fingers.

The inconsistencies in the use of commas and points to separate groups of digits or whole numbers from fractional parts when writing about money is one of several examples of cultural differences in mathematics. Countries colonized or influenced by Britain (including the USA, India and Malaysia) use a comma to separate blocks of three digits, whereas countries colonized or influenced by continental European countries (including South America and Vietnam) use a point. In Canada a comma is used in the English-speaking west of the country and a point in the French-speaking east. These types of considerations should be taken into account when working with families from other cultural backgrounds.

appendix − Roman Numerals

The numerals we use are called Hindu−Arabic numerals. Other people have used different systems for writing numbers.

The Romans used letters to write numerals. Their system is based on three principles.

1. The numbers 1, 5, 10, 50, 100, 500 and 1000 are each written using a single letter.



2. Addition and subtraction are used to construct further numerals.
   The numerals for 1 to 9 are listed below.



• When I is written before V, subtract 1 from 5 to get IV = 4.
• When I is written after V, add 1 to 5 to get VI = 6.
• When I is written before X, subtract 1 from 10 to get IX = 9.
• The same principle is used to construct the multiples of 10 from 10 to 90 and the multiples of 100 from 100 to 900.
• For example: XXX = 30XL = 40XC = 90
  CD = 400CM = 900
  
3. The numerals for the ones, tens, hundreds and thousands are calculated separately and then put together in order, with ones last. For example,

	23	= 20 + 3
		= XXIII

	49	= 40 + 9
		= XLIX

	399	= 300 + 90 + 9
		= CCCXCIX

	1997	= 1000 + 900 + 90 + 7
		= MCMXCVII

Roman numerals are often used to indicate the construction dates on buildings, the production dates of movies and books, and the numbers on some clocks and watches. There are some variations of this notation. For example IIII is sometimes used instead of IV. They are commonly used to number the preliminary pages of books, including the preface, foreword and table of contents.

ANSWERS TO EXERCISES

EXERCISE 1

The column labels in the base 2 system are 20, 21, 22, 23, ......

a 2 digits 0 and 1

b 37ten = 100101two

EXERCISE 2

a				b		2 × 100
						50
						6

 

The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.

The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.

© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/