The Improving Mathematics Education in Schools (TIMES) Project
- An understanding of the Hindu-Arabic notation and place value as applied
to whole numbers (see module, Using place value to write numbers). - Counting on by ones and skip-counting.
- An appreciation that addition can be modelled by combining sets of objects,
and also by movement to the right on a number line. - An understanding of, and fluency with, addition of two single-digit numbers.
- Experience with the use of doubles, near-doubles and tens complements in
addition exercises. - An appreciation of the commutativity and associativity of addition.
- Fluency with decompositions and tens complements.
For example, 3 + 7 = 7 + 3 (commutative law for addition) and (2 + 3) + 7 = 2 + (3 + 7) (associative law for addition).
For example, 10 = 1 + 9 = 2 + 8 = 3 + 7 etc.
Numeracy and literacy are essential skills in modern society. Of the four arithmetic operations on numbers, addition is the most natural and, historically, was the first operation developed. The ability to add numbers in your head is used in everyday life, when you play or watch sport and when you buy a couple of items at the shops.
While there are many labour-saving devices that will do calculations, a student will not develop a number-sense or a fluency with operations if they move to algorithms and calculators too quickly.
Formal or written algorithms are useful when larger numbers make mental calculations difficult. While there are many ways to solve problems using arithmetic, the commonly taught algorithms have remained in constant use because they are accurate and efficient.
Once an understanding of numbers has been developed, we can use calculators and computers with some confidence that any data-entry errors that are inconsistent with our number sense will be identified. A relatively common example of someone working without a sense of number is the person at the check-out who tries to charge you a large sum for an inexpensive item simply because the cash register tells them to, without pausing to think that perhaps the code for the item was incorrect.
Developing a solid understanding of addition is essential for understanding later ideas and topics including other arithmetic operations and algebra.
Addition algorithms should not be introduced until students have started to develop a familiarity with basic addition. This can be developed by giving students hands-on experiences, including the use of manipulatives and number lines, and practice with mental strategies for addition based on the basic properties of numbers.
Some mental strategies are more useful than others depending on the numbers used. Several levels of mathematical sophistication are evident amongst the selection of strategies explained here.
Adding two single-digit numbers
A review of the addition of single-digit numbers is essential to ensure students have achieved fluency. Lack of fluency is a serious impediment to their mathematical development because the addition of two single-digit numbers appears as an embedded process in so many arithmetic and algebraic calculations.
Adding a single-digit number to a two-digit number without carrying
The first step is to understand that this case simplifies to the case of adding two single-digit numbers. Using hands-on materials is necessary in the early stages. Students then need to mentally apply decomposition and associativity to produce arguments such as the following.
22 + 5 = 20 + 7 = 27
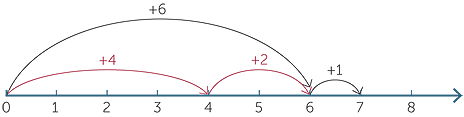
When children are using the number line, we can identify children that are still counting on by ones
from those that are skip-counting by fives.
Adding a single-digit number to a two-digit number with carrying
Once the previous case is mastered, students should be progressed to the extra complication of the need to carry a ten. In the first instance, students would use tens complements as illustrated below.
28 + 5 = 28 + 2 + 3 = 30 + 3 = 33.
On the number line, this corresponds to jumping to the first number, then jumping to the nearest ten above it, then jumping the rest of the way. The mental strategy essentially involves calculating the size of this last jump.
Alternative strategies should also be investigated. Different strategies should be recognized as equally valid and their relative merits discussed. In particular, students should be introduced to the process used in the standard algorithm in an informal way.
For example,
28 + 5 = 20 + 13 = 33
We observe that this argument reduces to two applications of adding two single-digit numbers, with one of the additions taking place in the tens column.
Adding two two-digit numbers with no carries involved
Mental strategies for adding two-digit numbers usually involve decomposing one of them and reducing the problem to one, or a combination of the cases already discussed. We illustrate this with the example 24 + 15.
First add ones then add tens.
This approach corresponds to
24 + 15 = 24 + 5 + 10 = 29 + 10 = 39
This is the approach that is formalised in the standard algorithm. On the number line, this corresponds to skip-counting as illustrated below.
First add tens then add ones.
This involves the calculation
24 + 15 = 24 + 10 + 5 = 34 + 5 = 39
This is a valid approach. There is a formal algorithm known as the Hindu scratch method. This will be considered later in this module. Indeed, developmentally it often comes before the previous technique.
On the number line this corresponds to implementing the second and third jumps above in the opposite order.
Adding two two-digit numbers with carrying involved.
The next level of complication involves introducing carrying. We illustrate various techniques using 28 + 15.
First add ones then add tens
28 + 15 = 28 + 5 + 10 = 33 + 10 = 43
First add tens then add ones
28 + 15 = 28 + 10 + 5 =38 + 5 = 43
This technique requires revisiting the tens after the ones have been dealt with. Algorithmically, it is implemented as the Hindu scratch method described later in this module.
Build to tens
In this technique we decompose one number to create a tens complement for the other. This can usually be done in more than one way. For example
28 + 15 = 28 + 2 + 13 = 30 + 13 = 43
and
28 + 15 = 23 + 5 + 15 = 23 + 20 = 43
CLASSROOM ACTIVITY
Write the following numbers on the whiteboard.
60
132142189755
Write the numbers 0 to 20 on stickers and place them randomly around a beach ball. Pass the beach ball around the class. The person who catches the ball adds the number that lands nearest their right thumb to one of the numbers selected by the teacher from the list above and states which of the strategies for addition they have used.
A variation might be for the teacher to choose the strategy to be used.
Addition satisfies various properties that make calculations easier. The most commonly known law is the commutative law that says, for example, that
3 + 4 = 4 + 3.
It is a mistake to take commutativity for granted or think of it as a trivial observation. Note that subtraction is not commutative (3 − 4 ≠ 4 − 3). In particular, we observe a geometric difference between 3 + 4 and 4 + 3 on the following number lines even though the arithmetic outcome is the same.
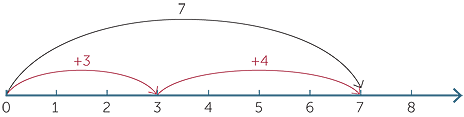3 + 4 corresponds to
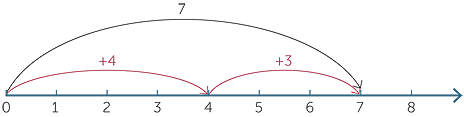4 + 3 corresponds to
An algorithm works most efficiently if it uses a small number of steps that apply in all situations. So algorithms do not resort to techniques, such as the use of near-doubles, that are efficient for a few cases but useless in the majority of cases. The benefit of an algorithm is that it can become an automated process that, once understood, provides an accurate and efficient means to find an answer. No algorithm will help you to add two single-digit numbers. It is essential that students are fluent with the addition of two single-digit numbers before embarking on any formal algorithm for addition.
As soon as you start using the standard algorithm to add more than two numbers, you need to be able to add a single-digit number to a two-digit number in the implementation of the algorithm.
Standard Algorithm
As a procedure the standard algorithm works in the following steps:
- Align the digits in the numbers into columns according to place value.
- Draw a line under the last number you are adding and put a + somewhere to note which operation you are performing.
- Starting from the rightmost column and working from right to left, perform the following subprocedure for each column.
- Add the digits in the column, including any carry digits.
- Write the units digit of your answer in the same column, but under the line.
- Make a note of any carry digits in the next column to the left.
Depending on where you mark your carry digits, the standard algorithm comes in versions exemplified by
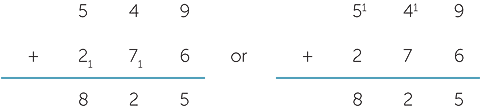
The digits are aligned in columns to ensure that like terms are added. In the standard algorithm, the location of the carry digits are habitual, as is the noting and location of the + sign.
CLASSROOM ACTIVITY
Rather than give students slabs of ‘add-ups’ to do, the following method of finding palindromes requires the use of an addition algorithm.
A palindrome is a word, sentence or number that reads the same backwards as it does forwards. For example, Hannah, 2 437 342 and “Ma, I am a llama, I am!”
We can create palindromes by following a procedure that starts with almost any number.
Start with any positive integer, reverse it and add the two numbers. Repeat the procedure until the sum of the two numbers is a palindrome.
For example, 64 generates a palindrome in 2 steps:
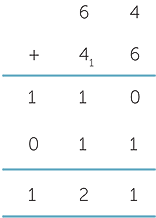
Try starting with the numbers 12, 32, 39, 76, 79, 256 and 73 187.
It could take 6 or more steps to get to a palindrome, but while they are searching for a palindrome, your students are practising their addition!
Some numbers take a great many steps, for example 89 takes 24 steps to reach the palindrome 8 813 200 023 188. There are 12 numbers less than 1000 that lead to this palindrome. Other numbers such as 196 seem to never lead to a palindrome but this has not been proved.
Common Errors
Misaligned columns
A common early error is to misalign the columns. For example, miscalculating 278 + 54 by writing
Entering a two-digit number into a single column.
Another common error is to enter a two-digit number into a single column, thereby destroying the place-value alignment in the solution. For example,
Forgetting to add the carry digits in the calculation.
For example,
Adding several numbers together.
Adding within columns
When implementing the algorithm to add two numbers, the most complicated process we face when adding a column of digits is the sum of two single-digit numbers. When we use the algorithm to add more than two numbers, we may have to use mental arithmetic to add a single-digit number to a two-digit number when adding the digits in a column. Consider the following example.
When adding the digits in the ones column we calculate 3 + 9 = 12 and then 12 + 6 = 18. Similarly, when adding the digits in the tens column we also need to use mental arithmetic to add a single-digit number to a two-digit number.
Higher carry digits
In some cases, the carry digits are greater than 1.
When we add a long list of numbers, the sum of a column may be a three-digit number. In this case we will need to add a single-digit number to a three-digit number, and the carry will be a two-digit number.
The Hindu scratch method
The Hindu scratch method starts from the left and adjusts previous terms as it progresses. It links naturally to mental arithmetic. It is hard to illustrate the method in a static way, but the final version of a calculation would look something like the following.
Start from the left.
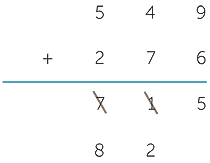
If there is no carrying then it is impossible to distinguish the use of the Hindu scratch method from the standard algorithm by looking at the finished product. You can only tell the Hindu scratch method has been used if there is carrying involved. In particular, children often intuitively use the Hindu scratch method with nobody noticing until carry digits are needed. Students using the Hindu scratch method often have a good understanding of addition; they are unlikely to have been taught the method and are likely to have developed it on their own.
Students found to be using the Hindu scratch method should not be told they are incorrect, but should be encouraged to use the standard algorithm as it is more efficient.
Further Mental Strategies − the associative law
and the any-order property
As well as being commutative, addition is associative, meaning that for all numbers a, b and c
a + (b + c) = (a + b) + c
Because of the associative law we have
4 + (2 + 1) = (4 + 2) + 1
4 + (2 + 1) corresponds to
whereas
(4 + 2) + 1 corresponds to
The combined effect of commutativity and associativity can be described in the following way.
The any-order property of addition
A list of whole numbers can be added two at a time in any order to give the same result.
We often use the any-order property in mental arithmetic, even when implementing the algorithm. For example, when calculating 71 + 68 + 49 + 32 most of us would naturally pair the tens complements to make the calculation easier:
71 + 68 + 49 + 32 |
= (71 + 49) + (68 + 32) |
| = 120 + 100 | |
= 220 |
|
CLASSROOM ACTIVITY
Find these sums by pairing the tens complements and rearranging to make the calculation easier.
a
24 + 7 + 32 + 6 + 93 + 8 =
b 98 + 49 + 17 + 11 + 32 + 43 =
c 333 + 54 + 145 + 7 + 55 + 6 =
Addition is the foundation of arithmetic. One way to model multiplication of whole numbers is as repeated addition. Subtraction is the inverse process of addition and division is the inverse process of multiplication. Thus in a very real sense, mastery of addition underpins success in all of arithmetic.
A strong number-sense is an invaluable advantage in the understanding of algebra. In particular, the process of decomposing and recombining numbers aids the understanding of general algebraic manipulations. A strong grounding in arithmetic sets a student up for success in algebra.
Addition, in the sense of measuring the size of combined sets, was probably done as soon as people counted. Addition itself does not change; 4+2 is six regardless of whether you write it as 6, VI or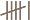 
. Just as the history of number is really all about the development of numerals, the history of addition is mainly the history of the processes people have used to perform calculations.
The development of the Hindu-Arabic place-value notation enabled the implementation of efficient algorithms for arithmetic and was probably the main reason for the popularity and fast adoption of the notation.
The word algorithm is derived from the name of Muhammad al- Khwārizmī an Islamic astronomer and mathematician. In 825 AD he wrote a treatise entitled Book on Addition and Subtraction after the Method of the Indians. It was translated into Latin in the 12th century as Algoritmi de numero Indorum. The term Algoritmi probably referred to
al-Khwārizmī rather than a general procedure of calculation, but the name has stuck.
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
Mathematical Circus, Martin Gardner, Penguin, (1970)
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
