The Improving Mathematics Education in Schools (TIMES) Project
- Facility with the arithmetic of fractions, decimals and percentages.
- Facility with converting fractions and decimals to percentages and vice versa.
- Facility with simple percentage problems.
- Familiarity with the basic operations on a calculator, including the power button xy.
- Familiarity with rounding numbers to a given number of decimal places, the nearest whole number, to the nearest ten, and so on.
- Facility with rounding money to the nearest dollar and to the nearest cent.
- Familiarity with the use of spreadsheets.
For most people, one of the primary applications of arithmetic is in dealing with money and in coping with questions involving financial computations. For example, when we are offered a 25% discount in a shop, we ought to be able to work out, at least roughly, what this will be and make sure we receive it. Similar calculations also apply to bank interest and commissions. If we are offered a 12% commission on sales of $3000, how much should we receive? Such simple problems should be able to be easily solved.
When buying a car, using a credit card, or deciding how good a particular ‘bargain’ is,
we all need to be competent in our understanding of commercial or consumer arithmetic. Otherwise we run the serious risk of wasting our money or, even worse, being at the mercy of unscrupulous individuals. This is particularly important when we come to the ‘big ticket items’ of life such as purchasing a car, a home or planning superannuation. It is also important when dealing with our tax returns.
This module will apply the arithmetical skills related to percentages, fractions, addition, subtraction, multiplication and division. Thus it gives practical applications of the ideas
and methods of arithmetic that students have been studying since primary school.
In most of the modules from F–8 we present the material so that the ideas can be understood and the exercises solved without using a calculator. For the work in this module, we assume that the reader has a calculator at hand, and that the answers to computations are rounded in a way that is appropriate in the given context. When presenting problems to school students it is wise for the teacher to specify carefully how they wish their students to round up or down, whether to the nearest dollar, or nearest cent and so on. Note that rounding at multiple stages in a calculation may alter an answer by a small amount. For this reason it is better to only round at the last step.
In the following sections, we will, for the most part, apply only two basic ideas. Finding a percentage of a number, and increasing or decreasing a number by a given percentage. Finding simple interest or commissions all involve multiplying a given number by a factor which will depend on the given percentage. Other problems often simply involve reversing the process. This can be done using division. For example, to increase a number by 15%, we multiply the number by 1.15, to reverse this process we simply divide by 1.15. We will see below that these ideas simplify a number of problems that students have traditionally found difficult.
A percentage is a way of writing a fraction with a denominator of 100.
Thus 10% means  which can be simplified to
which can be simplified to 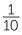 or as a decimal, 0.1.
or as a decimal, 0.1.
Since 100% =1, to convert a fraction or decimal to a percentage, we multiply by 100% .
For example,
![]()
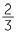 =
= 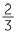 × 100% = 66
× 100% = 66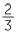 %
% ![]() and
and![]() 3.2 = 3.2 × 100% = 320%.
3.2 = 3.2 × 100% = 320%.
It is useful to be familiar with a number of commonly used fractions and their
percentage equivalents.
| Fraction | percentage | Fraction | percentage |
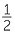 |
50% | 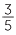 |
60% |
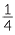 |
>25% | 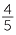 |
80% |
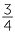 |
75% |  |
12.5% |
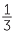 |
33 % % |
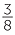 |
37.5% |
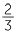 |
66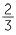 % % |
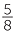 |
62.5% |
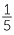 |
20% | 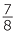 |
87.5% |
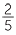 |
40% | 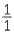 |
100% |
Percentage of a quantity
When told, for example, that 84% of a group of 250 people surveyed watched the cricket match on Saturday, it is natural to ask what exact number this was. To do this we find
84% of 250, which is 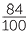 × 250 = 210 people.
× 250 = 210 people.
Also, if we know, for example, that 37 of the 50 people in the swimming club attended training, then it is useful to express this number as a percentage of the whole. This is
done by expressing 37 as a fraction of 50 and converting it to a percentage.
Thus, 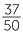 × 100 = 74%, so we can say that 74% of the club attended training.
× 100 = 74%, so we can say that 74% of the club attended training.
Exercise 1
Mike bought 72 stamps. He bought 27 more stamps than Carla. Express the number of stamps Carla bought as a percentage of the number Mike bought.
Reversing the Process
To find 15% of a given quantity, we multiply the quantity by 15%. To reverse the process, we divide by 15%. Thus, for example, if 15% of Paul’s take home pay is $90, then his take home pay was
![]() 90 ÷ 15% = 90 ÷ 0.15 = $600.
90 ÷ 15% = 90 ÷ 0.15 = $600.
This is a simple but important algorithm that is very useful in consumer arithmetic.
EXAMPLE
Sterling silver is an alloy that is made up of 92.5% by mass silver and 7.5% copper.
- a
- How much sterling silver can be made with 5kg of silver and unlimited supplies
of copper? - b
- How much sterling silver can be made with 5kg of copper and unlimited supplies
of silver?
Solution
- a
- Mass of silver = mass of sterling silver × 92.5%
Reversing this:
| mass of sterling silver | = mass of silver ÷ 92.5% | |
| =5 ÷ 0.925 | ||
| ≈ 5.405kg |
- b
- Mass of copper = mass of sterling silver × 92.5%
Reversing this:
| mass of copper | = mass of sterling silver ÷ 7.5% | |
| = 5 ÷ 0.075 | ||
| ≈ 66.667kg |
EXERCISE 2
A man earns $1440 for a 44 hour week. His weekly earnings are increased by 10%, but his hours are cut by 10%. What are his new earnings?
A commission is a fee charged for services rendered. For example, a real estate agent will charge a commission on the selling price of a house (in addition to such things as the fee for advertising the house), and a financial advisor will charge a commission for managing a portfolio of investments. Commissions are generally stated in the form of percentages.
For example, a gallery charges a commission of 6.5% for selling a painting. If they sold a painting for $180 000, how much did the owner receive?
| Commission | = 180 000 × 6.5% | |
| = 180 000 × 0.065 | ||
| = 11 700. |
Hence the owner receives 180 000 − 11 700 = $168 300.
This can also be calculated as 180 000 × 93.5%
On the other hand, suppose that the gallery received $3640 commission for the sale of a painting. What was the selling price of the painting?
This is a reverse process, so
| Selling price | = commission ÷ 6.5% | |
| = 3640 ÷ 0.065 = $56 000. |
A simple business model is to consider sales and costs. Sales refer to the income of the business and costs may include wages and rent.
Thus we can define
![]() Income − Expenditure = Profit/Loss
Income − Expenditure = Profit/Loss ![]() OR
OR![]() Sales − Costs = Profit/Loss.
Sales − Costs = Profit/Loss.
Clearly, if the difference above is positive then we have a profit and if it is negative, a loss.
EXAMPLE
Joshi’s tile shop made a profit of 5.8% on total costs last year. If the actual profit was
$83 000, what were the total costs, and what were the total sales?
solution
Profit = cost × 5.8%
| Reversing this, cost | = profit ÷ 5.8% |
| = 83 000 ÷ 0.058 | |
| ≈ $1 431 034, correct to the nearest dollar. |
| Hence | total sales | = profit + costs | |
| ≈ 83 000 + 1 431 034 | |||
| = $1 514 034. |
Income tax rates are often progressive. This means that the more you earn, the higher the rate of tax on each extra dollar you earn. Taxable income (which is the income after deductions) is divided into tax brackets. Since these can change from year to year, we will assume the following income tax brackets as an example.
- There is no tax on the first $12 000 that a person earns in the given year.
- From $12 001 to $30 000 the tax rate is 15c for each dollar over $12 000.
- From $30 001 to $75 000, the tax rate is 25c for each dollar over $30 000.
- Over $75 000, the tax rate is 35c for each dollar over $75 000.
Based on this schedule, the tax payable for a person earning, for example, $62 300 is calculated as follows:
![]() Tax on first $12 000 = $0
Tax on first $12 000 = $0
![]() Tax on next $18 000 = 18 000 × 0.15 = $2700
Tax on next $18 000 = 18 000 × 0.15 = $2700
![]() Tax on the remaining $32 300 = 32 300 × 0.25 = $8075
Tax on the remaining $32 300 = 32 300 × 0.25 = $8075
![]() Hence the total tax is $10 775.
Hence the total tax is $10 775.
EXERCISE 3
a![]() Use the tax schedule above to find the tax payable on a taxable income of $120 000.
Use the tax schedule above to find the tax payable on a taxable income of $120 000.
b![]() What percentage is this of the total taxable income?
What percentage is this of the total taxable income?
When money is borrowed, the borrower normally repays the amount they have borrowed plus another amount that is called the interest. The amount of interest usually depends on:
- the amount borrowed, called the principal,
- the rate at which the interest is charged,
- the time for which the money is borrowed.
The rate is almost always expressed as a percentage for each year. For example, the rate might be 5% per annum, or 5% p.a. The phrase per annum is the Latin for for a year.
In simple interest transactions, interest is paid on the original amount borrowed. It is calculated by finding the amount of interest on the principal in one year and multiplying it by the number of years. Thus, if P is the principal, r is the interest rate, expressed as a percentage per annum, and T is the number of years, then we have the well-known simple interest formula
![]() I = PrT.
I = PrT.
If the interest rate is expressed in terms of some other period of time, for example per month, then we will need to adjust T accordingly.
Thus, for example, the simple interest on $12 000 for 6 years at 8.25% is given by
| I | = PrT | |
| = 12 000 × 0.0825 × 6 | ||
| = $5940. |
Since the formula contains four pronumerals, specifying any three of them allows the fourth to be found.
EXAMPLE
Jessie borrows $3000 from her parents to help buy a car. They agree that she should only pay simple interest. Five years later she pays them back $3600, which includes simple interest on the loan. What was the interest rate?
Solution
The total interest paid was $600.
| So I | = 600, P = 3000 and t = 5 | |
| I | = PrT | |
| 600 | = 3000 × r × 5 | |
| 600 | = 15 000 × r | |
| r | = 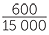 × × 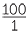 % % |
|
| = 4% |
Percentage Increase and Decrease
When a quantity is increased or decreased, the change is often expressed as a percentage of the original amount. The key to finding percentage increases and decreases is to combine two steps into one. Thus, for example, to increase 30 by 5% we can find 5% of 30, which is 1.5, and add it on to 30 to produce 31.5.
It is better, however, to combine the two steps and find 105% (= 100% + 5%) of 30,
which is
![]() 1.05 × 30 = 31.5.
1.05 × 30 = 31.5.
Hence, to increase a quantity by a% we multiply by (100 + a)%.
This key idea will be used repeatedly in the remaining work in this module.
EXAMPLE
The number of patient admissions at a certain hospital last year was 890 and increased by 23% this year. How many admissions are there this year?
Solution
We multiply 890 by 123%.
![]() So the number of admissions = 890 × 1.23 = 1094.7 ≈ 1095.
So the number of admissions = 890 × 1.23 = 1094.7 ≈ 1095.
Percentage decrease can also be calculated in one step. For example, if we wish to decrease a quantity by 30%, then we obtain 100 − 30 = 70% of the amount we started with.
Hence, to decrease a quantity by a% we multiply by (100 − a)%.
Again, this key idea will be used repeatedly in the remaining work in this module.
EXAMPLE
A government department was ordered to decrease its $2 000 000 budget by 3% in the coming year. How much did they have for their budget?
Solution
New budget = 2 000 000 × 97% = 2 000 000 × 0.97 = $1 940 000.
To find the rate of increase or decrease
Example
Suppose that the rainfall has increased from 480 mm p.a. to 690 mm p.a. What percentage increase is this?
Solution
Method 1
Consider the increased or decreased value as a percentage of the original value.
 |
= 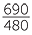 × × 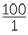 % % |
|
| = 143.75% |
So the rainfall has increased by 43.75%.
Method 2
Find the actual increase by subtraction, and then express the increase as a percentage of the original rainfall.
Increase = 210 mm
| Percentage increase | =  × × 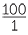 % % |
= 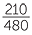 × × 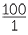 % % |
|
| = 43.75% |
Reversing the Process
Using the idea above, we can now solve problems which at first sight might appear rather hard. For example, after increasing my salary by 7%, I now receive $890 per week. What was my salary before the increase?
To increase by 7% we multiply by 107%. Hence to reverse the process, we divide by 107%. Thus, my original salary was
![]() 890 ÷ 107% = 890 ÷ 1.07 ≈ $831.78.
890 ÷ 107% = 890 ÷ 1.07 ≈ $831.78.
EXAMPLE
Shares in a particular stock fell 34% to $5.30. What was the price before the fall?
Solution
To decrease a quantity by 34% we multiply by (100 − 34)% = 66%. Hence to reverse the process, we divide by 66%. Thus, the value of the shares was
![]() $5.30 ÷ 66% = $5.30 ÷ 0.66 ≈ $8.03.
$5.30 ÷ 66% = $5.30 ÷ 0.66 ≈ $8.03.
In 1999 the Australian Government introduced a Goods and Services Tax, or GST for short. This tax applies to nearly all goods and services in Australia.
The current rate is 10% on the pre-tax price of the goods or service.
- When GST is to be added to the pre-tax price, we multiply by 110% = 1.1.
- If the quoted price includes the GST, the pre-tax price is obtained by dividing by 1.1.
EXAMPLE
The current GST rate is 10% of the pre-tax price.
a If a domestic plumbling job costs $630 before GST, how much will it cost after adding GST, and how much tax is paid to the Government?
b I paid $77 for an item recently. What was the price before adding GST, and what tax was paid to the Government?
Solution
The after-tax price is 110% of the pre-tax price.
| a | After-tax price | = 630 × 1.10 |
|
| = $693 | |||
| Tax | = 693 − 630 | ||
| = $63 | |||
| b | Pre-tax price | = 77 ÷ 1.10 |
|
| = $70.00 | |||
| Tax | = 77 − 7.00 | ||
| = $7 |
It is very common for a shop to discount the price of an item. Discounts are normally expressed as a percentage of the original price. Hence finding the price after a discount is the same as decreasing a quantity by a given percentage. As we have seen before, the process can also be reversed.
EXAMPLE
The Elegant Shirt Shop is closing down and has discounted all its prices by 35%.
a ![]() What is the discounted price of a shirt whose original price is:
What is the discounted price of a shirt whose original price is:
![]() i
i ![]() $120
$120 ![]()
![]() ii
ii ![]() $75?
$75?
b ![]() What was the original price of a shirt whose discounted price is $92.30?
What was the original price of a shirt whose discounted price is $92.30?
Solution
a ![]() The discount price of each item is 100% − 35% = 65% of the old price.
The discount price of each item is 100% − 35% = 65% of the old price.
| i | Hence discounted price | = old price × 0.65 | ||
| = 120 × 0.65 | ||||
| = $78 | ||||
| ii | discounted price | = 75 × 0.65 | ||
| = $48.75 |
b From part a, discount price = old price × 0.65
| Reversing this, old price | = discounted price ÷ 0.65 | ||
| = 92.30 ÷ 0.65 | |||
| = $142 |
EXERCISE 4
A shoe store is offering a discount of 35% at its end of year sale. Find the original price of an item whose discounted price is $20.80.
Repeated Increase and decrease
The method of increasing or decreasing a quantity by a given percentage is very useful when several increases or decreases occur.
For example, if the population of a town is 30 500 and increases by 6% then 7% and finally 4.5% over a three year period, then the new population is 30 500 × 1.06 × 1.07 × 1.045 ≈ 36 150. Notice that to find the overall percentage increase on the original, we calculate 1.06 × 1.07 × 1.045 ≈ 1.185 and so the percentage increase is about 18.5%. This is somewhat larger than the sum of the three increases, which is 17.5%, and illustrates the fact that percentages cannot always be added.
The same method can be applied to repeated decrease.
EXERCISE 5
A discount of 8% was made on a product costing $550. A further discount of 5% on the new price was then made.
a ![]() What is the cost now?
What is the cost now?
b ![]() What was the overall percentage discount?
What was the overall percentage discount?
The reverse method can again be applied.
EXAMPLE
Using the discounts in the above exercise, we find that an item costs $56 after the two discounts. What was the original price?
Solution
Method 1
After the first discount, the price was 100 − 8% = 92% of its original price.
After the second discount, the price was 100 − 5% = 95% of the discounted price.
Hence the final price was 0.92 × 0.95 = 0.874 = 87.4% of the original price.
Thus to find the original price, we divide $56 by 0.874 to obtain $64.07
Method 2
Let the original price be $x
| Then |
x × 0.92 × 0.95 = 56 |
| x = $64.07 |
EXERCISE 6
A bookstore has a 50% sale on all stock and then a further 16% reduction on all remaindered stock. A remaindered book is now selling for $10.50. What was its original price?
When an amount of money, called the principal, is invested in a bank, the bank generally pays interest at the end of each month and adds that interest to the account balance. Thus the balance, on which the interest is calculated, increases each month. This process is referred to as compound interest. In some situations the interest is paid yearly.
Adding on interest to a given amount is another example of increasing by a certain percentage and so the previous method again applies.
While there is a formula for calculating the final balance for a compound interest problem, when introducing compound interest it is best to avoid using the formula in the first instance.
EXAMPLE
Suppose we invest $2000 at 7.5% p.a. compounded yearly for 8 years. How much is in the account after the 8 year period?
Solution
After one year there will be 2000 × 1.075 = $2150
After two years there will be 2150 × 1.075 = $2311.25.
This last calculation can also be written as 2000 × 1.075 × 1.075 = 2000 × 1.0752.
Hence, after three years there will be 2000 × 1.0753 dollars and so on.
After 8 years there will be 2000 × 1.0758 ≈ $3566.96, to the nearest cent.
Thus the final balance is approximately $3566.96.
The bank has paid $1566.96 in interest and this corresponds to a simple interest rate of
![]() (1566.96 ÷ 2000) × 100 ÷ 8 = 9.7935%, per annum.
(1566.96 ÷ 2000) × 100 ÷ 8 = 9.7935%, per annum.
EXERCISE 7
If interest of 1% per month is compounded monthly for one year, to what rate of simple interest per annum is this equivalent?
Note then that when compound interest is being used, a 12% interest rate per year is not the same as a 1% interest rate per month, calculated monthly. The two rates are, however, close.
Reversing the Process
As always, the process can be reversed.
EXAMPLE
Eleni wants to borrow money for three years to start a business, and then pay all the money back, with interest, at the end of that time. The bank will not allow her final debt, including interest, to exceed $300 000. Interest is 9% p.a., compounded annually. What is the maximum amount that Eleni can borrow?
Solution
Each year Eleni will owe 109% of what she owed the previous year.
| Hence |
final debt | = original debt × 1.09 × 1.09 × 1.09 | |
| Reversing this, | original debt | = final debt ÷ (1.09)3 | |
| = 300 000 ÷ (1.09)3 | |||
| ≈ $231 655 |
Depreciation
Depreciation occurs when the value of an asset reduces as time passes. Assets such as cars, office furniture and computers typically lose value over time. Accountants generally assume that such assets decrease in value every year by the same amount, called the depreciation rate. For taxation purposes, the tax laws fix the depreciation rate for many standard assets.
Once again there is a formula for calculating the final value after depreciation, but it is best, when introducing the idea, to avoid using a formula in the first instance.
EXAMPLE
Suppose that a company bought a car four years ago for $40 000 and claimed a depreciation rate of 20% p.a. What is the value of the car after the four year period?
Solution
Since the depreciation rate is 20%,
after the first year, the value of the car = $40 000 × 80% = $32 000,
after the second year, the value of the car = $32 000 × 80% = $25 600.
These calculations can be combined as $40 000 × 80% × 80% = $40 000 × 0.82.
Similarly,
after the third year, the value of the car is $40 000 × 0.83, and
after the fourth year, the value is $40 000 × 0.84 = $16 384.
Hence the car now has a value of $16 384.
The process can also be reversed as the following exercise will show.
EXERCISE 8
St Scholasticus' Grammar School bought photocopying machines six years ago, which it then depreciates at 25% p.a. They are now worth $72 000.
a ![]() How much were they worth one year ago?
How much were they worth one year ago?
b ![]() How much were they worth two years ago?
How much were they worth two years ago?
EXERCISE 9
The number of trees on Green Plateau fell by 5% every year for 10 years.
Then the numbers rose by 5% every year for 20 years. What is the total percentage
gain or loss of trees over the thirty-year period?
Compound interest formula
We saw above how to compute compound interest via an iterative process. There is a straightforward formula for finding the value of an investment of $P, at an interest rate r per unit of time, over n units of time.
After 1 unit of time, the balance is P(1 + r).
After 2 units of time, the balance is P(1 + r)(1 + r) = P(1 + r)2.
Continuing the pattern, we can see that the formula for the amount A after n units of time is given by
![]() A = P(1 + r)n.
A = P(1 + r)n.
EXAMPLE
Suppose we invest $1000 compounded monthly at 0.5% per month for 2 years.
How much will the investment be worth after 2 years?
Solution
The given data is: P = 1000, r = 0.5% per month, and n = 2 × 12 = 24 months.
Hence A = 1000 × 1.00524 ≈ $1127.16.
Depreciation Formula
Earlier we used an iterative process to find the value to which an asset depreciates over a period of time. As with compound interest, there is a formula for calculating this.
Suppose we have an asset, originally worth $P, which depreciates at a percentage rate r per annum for n years.
After 1 year, the value of the asset is P(1 − r).
After 2 years, the value of the asset is P(1 − r)(1 − r) = P(1 − r)2.
Continuing the pattern, we can see that the formula for the value A of the asset after n years is given by
![]() A = P(1 − r)n.
A = P(1 − r)n.
EXAMPLE
Suppose that Abdul buys a computer for work for $3000 and claims a depreciation rate of 15% p.a. How much can he claim back on tax over a four year period?
Solution
The given data is: P = 3000, r = 0.15, n = 4.
Hence A = 3000 × 0.854 ≈ $1566.02.
Thus Abdul can claim $3000 − $1566.02 = $1433.98 in depreciation over four years.
Spreadsheets provide an excellent way to model financial calculations based on compound interest, because the successive steps in the compounding can be displayed in the successive lines of the spreadsheet.
When a formula is copied in a spreadsheet, the user can control whether each cell reference is an absolute reference of a relative reference. Relative references allow the recursive processes of financial calculations to be modelled easily and quickly.
Algebra is essential for spreadsheets, and nowadays spreadsheets are probably the most common application for algebra. For the simple applications of this module, cell references are used as pronumerals. There is no benefit in using a ‘name manager’ to define pronumerals.
This is a first treatment, and accordingly, interest is only calculated annually and installments are only paid annually. Spreadsheets, however, have an extremely large maximum size, and can easily cope with monthly or daily calculations.
Compound interest
EXAMPLE
On 31st December of Year 0, a principal of $12 000 is invested at a rate of 5% per annum for 12 years, compounded annually.
- a
- Design a spreadsheet to model the compound interest on this investment.
Design the sheet so that the interest rate and the principal can be changed quickly. - b
- How long does it take for the principal to increase by at least 50%?
- c
- What is the effect of doubling:
![]() i
i ![]() the principal
the principal ![]() ii
ii![]() the interest rate?
the interest rate?
- d
- What principal would yield a final balance of $50 000 at 5% per annum?
- e
- What interest rate would yield a final balance of $50 000 on a principal of $12 000?
Solution
| a | A | B | C | D | ||
| 1 | Principal | $12,000.00 | ||||
| 2 | Interest rate per annum | 5.00% | ||||
| 3 | year | Rate | Interest | Balance Dec 31 | ||
| 4 | 0 | 12,000.00 | ||||
| 5 | 1 | 5.00% | 600.00 | 12,600.00 | ||
| 6 | 2 | 5.00% | 630.00 | 13,230.00 | ||
| 7 | 3 | 5.00% | 661.50 | 13,891.50 | ||
| 8 | 4 | 5.00% | 694.58 | 14,586.08 | ||
| 9 | 5 | 5.00% | 729.30 | 15,315.38 | ||
| 10 | 6 | 5.00% | 765.77 | 16,081.15 | ||
| 11 | 7 | 5.00% | 804.06 | 16,885.21 | ||
| 12 | 8 | 5.00% | 844.26 | 17,729.47 | ||
| 13 | 9 | 5.00% | 886.47 | 18,615.94 | ||
| 14 | 10 | 5.00% | 930.80 | 19,546.74 | ||
| 15 | 11 | 5.00% | 977.34 | 20,524.07 | ||
| 16 | 12 | 5.00% | 1,026.20 | 21,550.28 | ||
| 17 | Final balance | 21,550.28 | ||||
| 18 | Total interest | 9,550.28 | ||||
In the table above, formatting is the first task:
The rates cells are formatted as percentages correct to two decimal places.
The principal at cell D1 is formatted as currency so that it has a dollar sign.
The other cells with amounts are formatted as numbers with two decimal places.
The cells in the year column are formatted as numbers with no decimal places.
The principal and the interest rates are entered in the first two rows, so that the values in those cells can be used in the table below. This allows quick experimentation with the whole sheet at a later stage simply by changing these two values.
In the ‘Year 0’ row, the entry at cell A4 is ‘0’, and the entry at cell D4 is =$D$1, so that the principal is automatically copied into cell D4.
The ‘Year 1’ row calculates the first year’s interest and the balance at the end of Year 1:
A5: =A4+1. This increases the year by 1.
B5: =$D$2. This copies the rate from cell D2.
C5: =D4*B5.This calculates the year’s interest by multiplying the balance in the previous line by the interest rate.
D5: =D4+C5. This adds the interest to the previous balance to give the balance at the end of Year 1.
We now copy the ‘Year 1’ row of the table into all the remaining rows. (This can be done using either the ‘copy-and-paste’ macro or the ‘fill down’ macro.) When this is done, the row numbers in the cell references change correspondingly, so that the balance models the growth of the investment.
A cell reference enclosed in dollar signs, like =$D$2, is an absolute reference and does not change when the formula is copied. A cell reference without dollar signs, like =A4+1, is a relative reference and is interpreted in terms of its position relative to the current cell, for example as ‘the cell above the current cell’ or as ‘the cell on the line above and two columns to the right’.
- b
- The balance has reached $18 000 after 9 years.
- c
- When the principal is doubled, all the balances and interest amounts are doubled. When the interest is doubled to 10%, the total interest increases by a factor of nearly 2.7 from $9550.28 to $25 661.14.
In Windows, the keyboard shortcut ‘Ctrl Z’ will undo any changes made to the spread- sheet. This command is extremely useful when experimenting with the data, as in this example and in the following exercise. - d
- Using the trial and error approach of changing the principal repeatedly, a principal of $27 842 yields a final balance of $50 000.23.
- e
- Using the trial and error approach of changing the interest rate repeatedly, an interest rate of 12.63% yields a final balance of $50 006.94.
EXERCISE 10
Adapt the spreadsheet to find the effects on the final balance when:
- a
- The principal changes to $10 000.
- b
- The interest rate changes to 10% on a principal of $10 000.
Superannuation
EXAMPLE
On 1st January each year for 20 years, an installment of $6000 is paid into a superannuation account. Interest is assumed to be constant at 6% per annum, and is paid into the account on 31st December each year.
- a
- Design a spreadsheet to model this investment.
- b
- How many years does it take for the balance to exceed half the final balance?
- c
- In what year did the interest earned first exceed the installment?
- d
- What are the effects of doubling:
![]() i the installment,
i the installment, ![]() ii the interest rate?
ii the interest rate?
- e
- What installment would yield a final balance of $500 000 at 6% per annum?
- f
- What interest rate would yield a final balance of $500 000 given installments of $6000?
Solution
| a | A | B | C | D | E | F | |
| 1 | Installment paid each year | $6,000.00 | |||||
| 2 | Interest rate per annum | 6.00% | |||||
| 3 | Year | Installment | Balance Jan 1 |
Rate | Interest | Balance Dec 31 |
|
| 4 | 0 | 0.00 | |||||
| 5 | 1 | 6,000.00 | 6,000.00 | 6.00% | 360.00 | 6,360.00 | |
| 6 | 2 | 6,000.00 | 12,360.00 | 6.00% | 741.60 | 13,101.60 | |
| 7 | 3 | 6,000.00 | 19,101.60 | 6.00% | 1,146.10 | 20,247.70 | |
| 8 | 4 | 6,000.00 | 26,247.70 | 6.00% | 1,574.86 | 27,822.56 | |
| 9 | 5 | 6,000.00 | 33,822.56 | 6.00% | 2,029.35 | 35,851.91 | |
| 10 | 6 | 6,000.00 | 41,851.91 | 6.00% | 2,511.11 | 44,363.03 | |
| 11 | 7 | 6,000.00 | 50,363.03 | 6.00% | 3,021.78 | 53,384.81 | |
| 12 | 8 | 6,000.00 | 59,384.81 | 6.00% | 3,563.09 | 62,947.90 | |
| 13 | 9 | 6,000.00 | 68,947.90 | 6.00% | 4,136.87 | 73,084.77 | |
| 14 | 10 | 6,000.00 | 79,084.77 | 6.00% | 4,745.09 | 83,829.86 | |
| 15 | 11 | 6,000.00 | 89,829.86 | 6.00% | 5,389.79 | 95,219.65 | |
| 16 | 12 | 6,000.00 | 101,219.65 | 6.00% | 6,073.18 | 107,292.83 | |
| 17 | 13 | 6,000.00 | 113,292.83 | 6.00% | 6,797.57 | 120,090.40 | |
| 18 | 14 | 6,000.00 | 126,090.40 | 6.00% | 7,565.42 | 133,655.82 | |
| 19 | 15 | 6,000.00 | 139,655.82 | 6.00% | 8,379.35 | 148,035.17 | |
| 20 | 16 | 6,000.00 | 154,035.17 | 6.00% | 9,242.11 | 163,277.28 | |
| 21 | 17 | 6,000.00 | 169,277.28 | 6.00% | 10,156.64 | 179,433.92 | |
| 22 | 18 | 6,000.00 | 185,433.92 | 6.00% | 11,126.03 | 196,559.95 | |
| 23 | 19 | 6,000.00 | 202,559.95 | 6.00% | 12,153.60 | 214,713.55 | |
| 24 | 20 | 6,000.00 | 220,713.55 | 6.00% | 13,242.81 | 233,956.36 | |
| 25 | Final balance | 233,956.36 | |||||
| 26 | Total installments | 120,000.00 | |||||
| 27 | Total interest | 113,956.36 | |||||
The installment and the interest rate are entered at the top of the spreadsheet and used below. The ‘Year 0’ row of the table sets the year to zero and the balance to zero.
The ‘Year 1’ row begins the recursive process. First, the installment paid on 1st January is added to the balance, then the interest for the year on that balance is calculated and added to the balance on 31st December:
A5: =A4+1 This increases the year by 1.
B5: =$D$1 This copies the installment from cell D1.
C5: =F4+B5 This adds the installment in B5 to the previous balance in F4.
D5: =$D$2 This copies the interest rate from cell D2.
E5: =C5*D5 This calculates the year’s interest on the balance in C5.
F5: =C5+E5 This adds the year’s interest to the previous balance in C5.
As before, the ‘Year 1’ row is now copied to all the remaining rows of the table. The cell references in each formula change accordingly, except for the absolute cell references.
- b
- The balance first exceeds half the final balance at the end of Year 13
- c
- The interest first exceeds the installment in Year 12.
- d
- When the installment doubles, all the amounts in the table double. When the interest rate doubles, the final balance rises from $233 956.36 to $484 192.41 and the total interest rises by a factor of nearly 3.2 from $133 956.36 to $364 192.41.
- e
- Using the trial and error approach of changing the installment repeatedly, an installment of $12 823 yields a final balance of $500 003.73.
- f
- Using the trial and error approach of changing the interest rate repeatedly, an interest rate of 12.26% yields a final balance of $500 179.98.
EXERCISE 11
Adapt the spreadsheet to find the effects on the final balance when:
- a
- The installment changes to $10 000.
- b
- The interest rate changes to 10% with installments of $6000.
Housing loans
EXAMPLE
Prasad and Isabella borrow $400 000 on 31st December to buy a house. They pay it off by annual installments of $36 000 paid every successive 31st December for 25 years. Interest is assumed to be 7.5% per annum, charged each 31st December.
- a
- Design a spreadsheet to model this loan.
- b
- What actually happens on 31st December of the last year?
- c
- How long does it take to reduce the loan to 75% of its original value?
- d
- What are the effects of:
![]() i
i ![]() doubling the installment,
doubling the installment, ![]() ii
ii ![]() halving the interest rate?
halving the interest rate?
- e
- What installment would pay the loan off in 15 years with the same interest rate?
- f
- With what interest rate would the loan be paid off in 20 years with the original installment?
- g
- What happens if $500 000 is borrowed with the same installments and interest rate?
Solution
a |
A |
B |
C |
D |
E |
|
1 |
Initial loan |
$400,000.00 |
||||
2 |
Instalment paid each year |
$36,000.00 |
||||
3 |
Interest rate per annum |
7.50% |
||||
4 |
Year |
Rate |
Interest |
Instalment |
Balance Dec 31 |
|
5 |
0 |
-400,000.00 |
||||
6 |
1 |
7.50% |
-30,000.00 |
36,000.00 |
-394,000.00 |
|
7 |
2 |
7.50% |
-29,550.00 |
36,000.00 |
-387,550.00 |
|
8 |
3 |
7.50% |
-29,066.25 |
36,000.00 |
-380,616.25 |
|
9 |
4 |
7.50% |
-28,546.22 |
36,000.00 |
-373,162.47 |
|
10 |
5 |
7.50% |
-27,987.19 |
36,000.00 |
-365,149.65 |
|
11 |
6 |
7.50% |
-27,386.22 |
36,000.00 |
-356,535.88 |
|
12 |
7 |
7.50% |
-26,740.19 |
36,000.00 |
-347,276.07 |
|
13 |
8 |
7.50% |
-26,045.71 |
36,000.00 |
-337,321.77 |
|
14 |
9 |
7.50% |
-25,299.13 |
36,000.00 |
-326,620.91 |
|
15 |
10 |
7.50% |
-24,496.57 |
36,000.00 |
-315,117.48 |
|
16 |
11 |
7.50% |
-23,633.81 |
36,000.00 |
-302,751.29 |
|
17 |
12 |
7.50% |
-22,706.35 |
36,000.00 |
-289,457.63 |
|
18 |
13 |
7.50% |
-21,709.32 |
36,000.00 |
-275,166.95 |
|
19 |
14 |
7.50% |
-20,637.52 |
36,000.00 |
-259,804.48 |
|
20 |
15 |
7.50% |
-19,485.34 |
36,000.00 |
-243,289.81 |
|
21 |
16 |
7.50% |
-18,246.74 |
36,000.00 |
-225,536.55 |
|
22 |
17 |
7.50% |
-16,915.24 |
36,000.00 |
-206,451.79 |
|
23 |
18 |
7.50% |
-15,483.88 |
36,000.00 |
-185,935.67 |
|
24 |
19 |
7.50% |
-13,945.18 |
36,000.00 |
-163,880.85 |
|
25 |
20 |
7.50% |
-12,291.06 |
36,000.00 |
-140,171.91 |
|
26 |
21 |
7.50% |
-10,512.89 |
36,000.00 |
-114,684.81 |
|
27 |
22 |
7.50% |
-8,601.36 |
36,000.00 |
-87,286.17 |
|
28 |
23 |
7.50% |
-6,546.46 |
36,000.00 |
-57,832.63 |
|
29 |
24 |
7.50% |
-4,337.45 |
36,000.00 |
-26,170.08 |
|
30 |
25 |
7.50% |
-1,962.76 |
36,000.00 |
7,867.17 |
|
31 |
Final balance |
7,867.17 |
||||
32 |
Total installments |
900,000.00 |
||||
33 |
Total interest paid |
492,132.83 |
||||
There are three parameters to enter at the top of the spreadsheet − the initial loan, the annual installment, and the interest rate.
In the ‘Year 0’ row, the ‘Balance’ is = $E$1 because the account is in debit.
The ‘Year 1’ row begins the recursive process:
A6: =A4+1 This increases the year by 1.
B6: =$E$3 This copies the rate from cell E3.
C6: =E5*B6 This calculates the year's interest on the balance in E5. The interest is negative because it is a charge against the customer's account.
D6: =$E$2 This copies the installment from cell E2.
E6: =E5+C6+D6 This adds the year's interest (a negative number) and the installment (a positive number) to the previous balance from E5 to give the new balance on 31st December.
The ‘Year 1’ row is now copied to all the remaining rows of the table. The cell references in each formula change accordingly, except for the absolute cell references.
- b
- The final payment required is not the full installment of $36 000, but only $28 132.83
- c
- The loan is first reduced below $300 000 at the end of the 12th year.
- d
- When the installment is doubled, the loan is paid off in 8 years, with $38 747.58 left over.
When the interest rate is halved, the loan is paid off in 15 years, with $12 768.74 left over. - e
- The installment should be about $45 315.
- f
- The interest rate should be about 6.25%.
- g
- Instead of the loan being paid off, it grows to about $602 000 over 25 years.
EXERCISE 12
Adapt the spreadsheet to find the effects on the term of the loan when:
a ![]() The installment changes to $50 000.
The installment changes to $50 000.
b ![]() The interest rate changes to 4%.
The interest rate changes to 4%.
To deal with more complicated financial problems such as superannuation and time payments, we need to understand what a geometric series is and how to find the formula for the sum of a geometric series.
A geometric sequence (or geometric progression) is a list of numbers in which each is obtained by multiplying the previous one by a constant multiplier called the common ratio. For example, the sequence 2, 6, 18, 54, 162, … is an example of a geometric sequence in which the common ratio is 3. When we add the numbers in a geometric sequence up to some point, we obtain a geometric series.
Hence the series 2 + 6 + 18 + 54 = 80 is the sum of the first four terms of the geometric sequence given above.
As above, we define a geometric series to be the sum of numbers in which each term is a constant multiple of the previous one. We will right the first term as a and the constant ratio as s. Hence the series can be written as
![]() Sn = a + as + as2 +… + asn − 1,
Sn = a + as + as2 +… + asn − 1,
and contains n terms. Series such as this arise naturally in financial (and many other) problems. We would like to obtain a simple formula for this sum. To do this we multiply both sides by s, thus
![]() sSn = as + as2 + … +asn.
sSn = as + as2 + … +asn.
If we now subtract these equations, most of the terms cancel and we obtain
![]() sSn − Sn = asn − a.
sSn − Sn = asn − a.
Factoring, (s − 1)Sn = a(sn − 1), and so Sn = 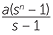 .
.
This is the formula for the sum to n terms of the geometric series with first term a and constant ratio s.
Superannuation is a way of saving for retirement. Money is regularly invested over a long period of time and (compound) interest is paid.
Suppose that I am to invest in a superannuation scheme for 30 years which pays 6% p.a. I put $3000 each year into the scheme, and (for the sake of simplicity) we will suppose that the interest is calculated yearly. Thus, the first $3000 will be invested for the full 30 years at 6% p.a. Hence it will grow to accrue to $3000 × 1.0630.
At the beginning of the next year, the next $3000 will be invested for 29 years and so will accrue to $3000 × 1.0629 and so on. Writing the amounts from smallest to largest, the total value of my investment will this be:
![]() A = $3000 × 1.06 + $3000 × 1.062 + … + $3000 × 1.0630.
A = $3000 × 1.06 + $3000 × 1.062 + … + $3000 × 1.0630.
This is a geometric series with a = $3000 × 1.06, and s = 1.06 and n = 30.
Substituting into the formula, the value of the sum is
![]() A =
A = 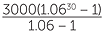 ≈ $237 174.56.
≈ $237 174.56.
This example illustrates both the value of regular saving and the power of compound interest − $90 000 invested becomes roughly $237 000 over 30 years.
Dealing with time payments is somewhat more difficult and the reader may wish to skip over this section. On the other hand, those who are paying off loans may find it useful.
It is, of course, too advanced for junior high school. Spreadsheets were used in a previous section.
When a loan is taken out, the amount borrowed (the principal) is generally repaid, along with the interest accrued, in equal installments. The interest depends on the balance owing and so will decrease over time as more payments are made.
Finding the amount of each repayment to be made, given that we wish to pay out the loan in a given time, appears at first sight to be a difficult problem, but it can be solved using geometric series.
Suppose, for example, that a car loan for $7000 is taken out at an interest rate of 6.2% p.a. (calculated monthly) and that the loan is to be repaid in 5 years with monthly repayments. How much should each monthly payment be, in order to pay out the loan in this time?
Since we are working in months, the period of the loan is 5 × 12 = 60 months, and the interest rate per month is approximately 6.2% per month. (Recall that for compound interest, a 12% p.a. rate is not exactly equal to a 1% per month rate.)
Hence r ≈ 0.0051667. To simplify the notation we will write
![]() R = 1 + r = 1.0051667.
R = 1 + r = 1.0051667.
Let P be the amount of each repayment, and Ak be the amount owing after k payments. After each month we owe R times the amount owing in the previous month (the balance plus the interest) minus P (the monthly repayment).
Hence
| A1 = 7000R − P | ||
| and so | A2 = R(7000R − P) − P = 7000R2 − P(1 + R). |
Continuing this process,
![]() A3 = R[7000R2 − P(1 + R)] − P = 7000R3 − P(1 + R + R2) (check this step carefully.)
A3 = R[7000R2 − P(1 + R)] − P = 7000R3 − P(1 + R + R2) (check this step carefully.)
From here we can see where the pattern is leading, so after n months,
![]() An = 7000Rn− P(1 + R + R2 + … + Rn − 1).
An = 7000Rn− P(1 + R + R2 + … + Rn − 1).
The sum inside the parentheses is a geometric series consisting of n terms with a = 1 and s = R. We can thus apply the formula for the sum of a geometric series to obtain
![]() An= 7000Rn− P
An= 7000Rn− P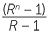 .
.
Now after 60 months, the loan has been repaid and so An=0, when
substituting the values of R = 1.0051667, n = 60, An=0, we obtain
0 = 7000 × 1.00516670 − P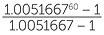 , and we can solve this for P to obtain
, and we can solve this for P to obtain
![]() P ≈ $135.98.
P ≈ $135.98.
Hence, we need to pay $135.98 per month in order to pay out the loan.
Note then that we have to repay a total of 60 × 135.98 = $8158.80 and so the total interest paid is $1158.80.
It appears that the concept of 'money’ arose in very ancient times via the need for an intermediary stage in the barter process. Thus, if I wish to exchange some barley for someone’s fruit, but the barley harvest has not yet come, I can hand over some other good such as metal, cattle, salt or wine, which I can then redeem when the barley has been harvested. This is referred to as commodity money. Thus metal, which is very durable, came, in time, to represent the basis for our modern concept of money.
In the first half of the seventh century BC, Pheidon of Argos, on the Greek mainland, is believed to have set up a system of standardized weights and measures, and to have begun the use of stamped coinage. Although this was the first use of coinage in Europe, the earliest known coins stem from Ionia (part of modern day Turkey) and by 650 BC stamped coinage was in relatively common usage in Lydia in Asia Minor from where the concept spread to most parts of Greece and beyond. Coins were typically minted by some official government process with the amount of precious metal being carefully controlled to equal the 'value’ of the coin. In time, the 'authority’ of the government stamp enabled the coin to be devalued in terms of the precious metal it contained, while nevertheless retaining official value. This led to the notion of representative money.
The concept of lending money at interest is an old one and is mentioned in the ancient Code of Hammurabi (about 1760 BC). The Greek word for interest, tokos, is related to the word for 'giving birth’. Thus the ancients thought of money 'giving birth’ to money in the form of interest.
Banking in Europe arose after the time of the Crusades, since paying for soldiers, weapons, transport etc across large distances required the transfer of large amounts of money. This was achieved in the form of bills of exchange. By the time of the Industrial Revolution, the church rules forbidding usury, the lending of money at interest, appear to have been either forgotten or reinterpreted and the lending of money at interest became very widespread.
It is worth commenting that the father of the famous Fibonacci (Leonardo of Pisa, c. 1202 AD) was a business man and that the young Leonardo assisted his father in his bookkeeping at an extremely young age. Many of the problems in Fibonacci’s Liber Abaci involve calculations with interest and percentages and are often couched in a financial setting.
There is some debate as to the origin of the % sign, however the word percentage is derived from the Italian per cento meaning out of a hundred.
It is interesting to note that the number e (≈ 2.71828 to 5 decimal places) which occurs as the base of the natural logarithm in Calculus, was known at an earlier date, since it arises from a simple problem in compound interest. Suppose we invest say $1 at 100% p.a.,
(a rather generous rate indeed!), compounded over n equal units of time during a one year period. The formula 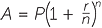 , where P = 1 is the amount invested, r = 1 is the interest rate per annum, n is the number of units of time, and A is the amount we have, becomes
, where P = 1 is the amount invested, r = 1 is the interest rate per annum, n is the number of units of time, and A is the amount we have, becomes 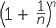 . If we calculate this quantity for larger and larger values of, we get closer and closer to the number 2.71828…. Using limit techniques we can show that this limit is equal to the number e. Thus, the most interest we can make from this scenario is about $1.72 (!)
. If we calculate this quantity for larger and larger values of, we get closer and closer to the number 2.71828…. Using limit techniques we can show that this limit is equal to the number e. Thus, the most interest we can make from this scenario is about $1.72 (!)
While there were earlier works written on the arithmetic of money, percentages and simple interest, it was in 1613 that Richard Witt produced a book entirely devoted to compound interest.
In 1847 the French Central Bank attempted to control interest rates through the manipulation of the money supply. This practice continues today via central banks such as the Reserve Bank of Australia.
Today, modern banking is a very complicated activity which employs highly trained mathematicians as financial and risk analysts.
In 1973 the Black-Scholes model for financial markets and derivative investments was put forward. This involved some quite sophisticated Mathematics that makes use of partial differential equations and is very important in the modern financial world. Modern actuarial and financial studies at tertiary level involve material from a number of branches of advanced Mathematics.
EXERCISE 1
62.5%
EXERCISE 2
$1425.60
EXERCISE 3
a ![]() $29,700
$29,700
b ![]() 24.75%
24.75%
EXERCISE 4
$32
EXERCISE 5
a ![]() $480.70
$480.70
b ![]() 12.6%
12.6%
EXERCISE 6
$25.00
EXERCISE 7
12.7% rounded to one decimal place
EXERCISE 8
a ![]() $96,000
$96,000
b ![]() $128,000
$128,000
EXERCISE 9
59% gain, rounded to one per cent.
EXERCISE 10
a ![]() $17,958.56
$17,958.56
b ![]() $31,384.28
$31,384.28
EXERCISE 11
a ![]() $389,927.27
$389,927.27
b ![]() $378,015.00
$378,015.00
EXERCISE 12
a ![]() The loan will be paid off on Dec 31 of the 13th year with a credit of $16,110.35.
The loan will be paid off on Dec 31 of the 13th year with a credit of $16,110.35.
b ![]() The loan will be paid off on Dec 31 of the 15th year with a credit of $471.75.
The loan will be paid off on Dec 31 of the 15th year with a credit of $471.75.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


