The Improving Mathematics Education in Schools (TIMES) Project

return to index

Subtraction of whole numbers

Number and Algebra : Module 8Years : 4-7

June 2011

PDF Version of module

Assumed Knowledge

• An understanding of the Hindu-Arabic notation and place value as applied to whole numbers (see module Counting and Place Value).
• An appreciation that subtraction can be modelled by removing objects from a set of objects, and also by a difference in sizes of two sets of objects.
• Familiarity with the use of the number line to model addition, as well as subtraction both as difference and as taking away.
• Counting forwards and backwards by ones and skip-counting on the number line.
• Understanding of, and fluency with, addition.
• Fluency with the calculation of all subtractions involving whole numbers up to and including 18.
• The use of complementary addition to perform simple subtractions. For example, for 15 − 7 = 8 , we recall 7 + 8 = 15.

Motivation

Of the four arithmetic operations on numbers, addition is the most natural and, historically, was the first operation developed. Subtraction and addition are inverse operations. For example 60 − 3 = 57 is equivalent to 60 = 57 + 3.

Subtraction answers questions such as:

1

A class has 30 students and 16 of them are girls. How many boys are there in the class?

2

I have $100 and I spend $20. How much do I have left?

3

Terry has 11 chocolates and Marie has 7. How many more chocolates does Terry have?

These questions are examples of three different types of question that require subtraction for their solution. A way of classifying questions that require subtraction for their solution is addressed in the Content section.

Content

The addition table

It is essential that students can do all the subtractions implicit in the addition table for two single-digit numbers.

Before moving on to subtraction algorithms, students need to be fluent in all subtractions for which the addition table of single-digit numbers provides the complementary additions. For example, both 13 − 5 = 8 and 13 − 8 = 5 have the complementary addition 13 = 8 + 5.

We ask students to develop fluency with addition and subtraction involving whole numbers up to and including 20 (instead of 18 as is done in the addition table) because it is useful to learn and because fluency aids calculations.

Different ways of thinking about subtraction

The following three questions illustrate three types of questions that require subtraction for their solution.

1

Matthew is riding his bike to the shopping centre 18 kilometres away. He gets a flat tyre after travelling 13 kilometres. How much further is it to the shopping centre?
We calculate the missing part as 5 kilometres.

2

Jenny has ten apples in a bowl and gives three apples to Fred. How many apples does Jenny have left? To solve this we think of taking three away from ten and conclude that Jenny has seven apples left.

3

Harry is 123cm tall and Ally is 112cm tall. How much taller is Harry than Ally?
We calculate the difference between Harry’s height and Ally’s height and conclude Harry is 11cm taller than Ally or Ally is 11 centimetres shorter than Harry.

The three questions given above, and the three questions in the Motivation section, are examples of three different types of situations where subtractions arise. These are sometimes called:

1

Part−whole (or adding on): A part of a set or quantity is specified and it is required to find how much is needed to make it ‘whole’.

2

Take−away: Objects are removed from a set or a measurement is decreased by a specified amount.

3

Difference: Two sets or two measurements are compared. In this case subtraction is interpreted as difference.

The number line and subtraction

Subtracting by ‘taking away’

If you have 5 items and you take 2 away, the number remaining is 5 − 2, which is 3.
For example, ‘I had 5 pencils but my sister took 2 away, so now I have 3’.

In this case, 2 is subtracted from 5 to give 3. On a number line, this can be illustrated
as shown.

5 − 2 = 3

With larger numbers this might be done by counting backwards (to the left) by ones or taking the correct number of steps to get to the solution.

Subtracting by “adding on”

Another way of thinking about the subtraction 5 − 2 is to ask “What do you add to 2 in order to get to 5?” This can also be illustrated on the number line.

2 + 3 = 5 so 5 − 2 = 3

One example of this is “I have 5 pencils and my brother has 2, so I have 3 more pencils than my brother”.

With larger numbers we might count forwards (to the right) by ones the number of steps to get to the number we want. The solution is the number of steps we took. When we think of subtraction in this way, we are using complementary addition.

Mental strategies for subtraction

Our choice of approach for subtraction depends on the numbers involved.
We usually calculate 20 − 17 using complementary addition, whereas we calculate
20 − 3 directly by taking away. Both correspond to the same addition fact, 20 = 17 + 3.

Once students start using an algorithm, they might be less likely to develop new mental strategies. It is therefore important that students are given the opportunity to develop a variety of useful mental strategies before a standard algorithm is introduced.

Single digit subtraction with no change to ‘columns’

When a student sees 68 − 5, they must recognize that the mental calculation is not
much more complicated than 8 − 5 and conclude that 68 − 5 = 63. In doing so,
they are mentally decomposing 68 and calculating

68 − 5 = 60 + (8 − 5) = 63

Decomposition is a basic component of all subtraction algorithms.

Single digit subtraction with change to ‘columns’

Students should be asked to consider calculations such as 62 − 5 = 57 and be encouraged
to perform the subtraction in different ways, including:

• Counting backwards and keeping track of the steps.

For example,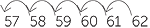

• Breaking the number apart into manageable steps.

For example, 62 − 5 = 62 − 2 − 3 = 60 − 3 = 57

• A different decomposition.

Would be, 62 − 5 = 50 + (12 − 5) = 57

Subtraction by equal addition

The principle of equal addition is the observation that if you add the same amount to two numbers, their difference does not change.

In the example, 37 − 18 = 39 − 20 = 19, we have added 2 to both 37 and 18 to make the calculation easier.

Note that the principle of equal addition also tells us that if you subtract the same amount from two numbers their difference doesn’t change. This can be used in a mental subtraction such as

115 − 65 = 100 − 50 = 50 or 115 −65 = 110 − 60 = 50.

Standard Subtraction Algorithms

We need an algorithm for subtraction, just as we have an algorithm for addition. Algorithms must be robust − in the sense that, they must be easy to remember and implement.

In all versions of the subtraction algorithm we write the larger number which we call the 'top number' above the smaller number which we call the 'bottom number'.

The simple case

When each digit in the ‘bottom number’ is less than or equal to the digit in the ‘top number’, you simply subtract in each column.

The general case

We need to deal with subtractions such as 81 − 27 = 54

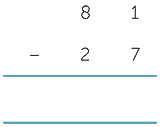
where the 7 is greater than the 1. There are several standard approaches to this, and we discuss the two most common.

The equal addition method (also known as ‘borrow and pay back’)

This method is based on the observation that adding 10 to both numbers does not change the difference between them. So we write

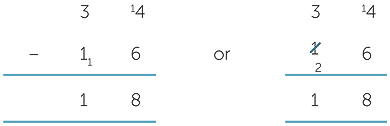
to mean that we add ten ones to 34 and one ten to 16. The algorithm works because, arithmetically, we are actually subtracting 26 from 44. The difference between 44 and
26 is the same as the difference between 34 and 16.

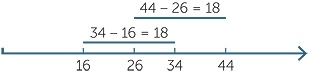
In the subtraction below, we are adding ‘ten tens’ to the top line and adding one hundred to the bottom line.

If there are many zeroes, we may need to perform equal addition in several columns before we can complete the calculation, as illustrated below.

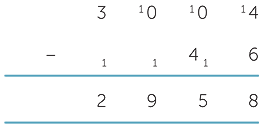
The traditional terminology for equal addition, “borrow and pay back”, is an unfortunate term because it does not accurately describe the process. The phrase “add the same to both numbers” is a more accurate description of the equal addition principle.

Decomposition method (also known as ‘trading’)

The names trading and decomposition come from the place-value representation of the numbers, as modelled by Diene’s blocks (MAB). The subtraction of one from the tens column and addition of ten to the ones column can be viewed as the “long” block being traded for, or decomposed into, ten “ones”.

We calculate 34 − 16 by writing 34 as 20 + 14 instead of 30 + 4.

	34 − 16	= (20 + 14) − (10 + 6)
		= (20 − 10) + (14 − 6)
		= 10 + 8

Algorithmically, we indicate the new regrouping as a conversion of one ten into ten ones.

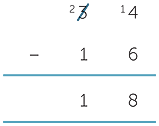
Consider the following calculation.

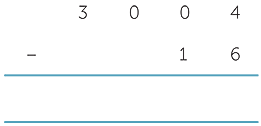
This can get messy using the decomposition method if you don’t have a good number sense. We could implement the calculation one column at a time, but this is time consuming and can get untidy and hard to follow. It is sometimes referred to as cascading trades. For example,

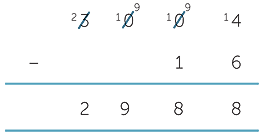
People often say 'I haven’t got any tens’. But in fact they have 300 tens! The key is to think of the 3000 as 300 tens and shift one of the tens over to the ones column, leaving you with 299 tens.

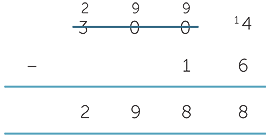
This way the calculation looks clean, is fast and is easy to check. All subtraction problems can and should be checked by adding the answer to the bottom number.

The advantages and disadvantages of the equal addition and decomposition algorithms

An advantage of the equal addition method is that it is easier to use and produces a tidier and less cluttered layout. A disadvantage of the method is that the mathematics underpinning the technique has an extra layer of complexity.

An advantage of the decomposition method is that it is initially easier to explain, especially using place-value blocks. The algorithm depends on expressing one number in a more convenient format. A disadvantage is that the layout can get messy, mainly because of all of the markings, and this can lead to more errors.

The relationship between subtraction and addition

We can use complementary addition to solve subtraction problems because subtraction is the inverse operation to addition. To “undo” an addition we perform the corresponding subtraction and vice-versa. This relationship makes it tempting to assume subtraction behaves in a similar way to addition, but the assumption is incorrect and this thinking can be the source of many errors in arithmetic.

The any-order property of addition is a consequence of two properties.

• Addition is commutative, in the sense that a + b = b + a for all whole numbers a and b. For example, 14 + 6 = 6 + 14
• Addition is associative, in the sense that (a + b) + c = a + (b + c) for all whole numbers a, b, and c. For example, (3 + 2) + 6 = 3 + (2 + 6)

Subtraction is not as well-behaved as addition.

Subtraction is not commutative. For example, 2 − 4 ≠ 4 − 2

Subtraction is not associative. For example, 6 − (4 − 1) ≠ (6 − 4) − 1

In particular, the any-order property of addition does not transfer to subtraction. With subtraction, the order in which operations are performed is critical. Failing to observe
and understand this can cause many arithmetical errors.

Links Forward

Subtraction is a fundamental operation. A mastery of arithmetic including subtraction, provides a firm foundation for algebra and functions.

Fluency with subtraction is essential for division. Division can somtimes be thought of as repeated subtraction. Subtraction is used when we perform division calculations, especially when we carry the division algorithms.

The principle of equal addition can be used to reduce subtraction of integers to a
two-step problem involving addition and subtraction of whole numbers. For example,
−4 − (−6) = 2 − 0 = 2.

Consumer arithmetic contains a wealth of applications of subtraction. These range from basic calculations, such as finding the change in a financial transaction, to calculating discounts and mortgage repayments.

History

The early development of subtraction is not documented because it is essentially prehistoric. The oldest written records of mathematical calculations date back over 4000 years to the ancient Egyptians and Babylonians. These documents include subtraction problems, so we know that subtraction as an operation was already used by then.

As with all arithmetic, the use of the Hindu-Arabic place value system enables the development of efficient algorithms.

The two algorithms discussed in this module and variations of them have been used for many centuries in Europe and Asia. In the Crafte of Nombryge (circa 1300 AD) one of the earliest books in English on the algorithms, there is a description of the subtraction of 1134 from 2122. This was working on the top line where the first step was to take 4 from 10 and then add 2. The ‘2’ in the ‘tens place’ is then changed to a ‘1’ and so on.

Variations of the other algorithms were also used in earlier centuries. For example, Borghi (1484), Fibonacci (1202) and Maximus Planudes (circa 1340) used these methods.

Johannes Widman was the author of an early book on arithmetic, published in German in 1489. This book has become famous since it contains the first appearance of + and − signs for addition and subtraction.

The following method did not find favour from arithmeticians until the nineteenth century. It was used in Austrian arithmetic books in the middle of the nineteenth century.

Austrian Method of Subtraction

The Austrian method of subtraction involves only addition. Add from the amount to be subtracted up to the next 'place value column', then to the next and so on.


References

History of Mathematics, D. E. Smith, Dover publications New York, (1958)

Man and Number, Donald Smeltzer, Adam and Charles Black, London, (1965)

Elementary Mathematics for Teachers, Thomas Parker and Scott Baldridge, Sefton-Ash Publishing, Michigan, USA, (2004)

ANSWERS TO EXERCISES

EXERCISE 1

a 84 b 118 c 3 d 36

EXERCISE 2

a 1518

 

The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.

The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.

© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/