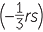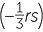The Improving Mathematics Education in Schools (TIMES) Project
Negatives and the Index Laws in Algebra
Number and Algebra : Module 24 ![]() Years : 7-8
Years : 7-8
June 2011
- The arithmetic of integers.
- Basic methods of mental arithmetic.
- Algebraic expressions with whole numbers.
- The index laws in arithmetic with nonzero whole number indices.
- The HCF and LCM in arithmetic.
The various uses of algebra require systematic skills in manipulating algebraic expressions. This module is the second of four modules that provide a systematic introduction to basic algebraic skills.
The first of these modules, Algebraic Expressions, introduced algebra using only whole numbers for pronumerals. The present module extends the methods of that module to integers and to simple positive and negative fractions, covering in turn substitution, collecting like terms, taking products, and expanding brackets using the distributive law. These first four sections of this module provide all the skills needed to solve straightforward linear equations, without the constraints of avoiding negative coefficients.
We saw the importance of the index laws when dealing with powers in the module, Multiples, Factors and Powers. Clearly the index laws need to be integrated into algebra. This module does not involve anything but very simple fractions, so it deals only with the three index laws involving products. The remaining two index laws are left until the next module, whose principal theme is the use of fractions in algebra.
Factoring will later become an essential part of algebra for a variety of reasons, most obviously because it can help us find which substitutions make an algebraic expression zero. The first step in factoring is taking out the HCF of an algebraic expression — applying the distributive laws in reverse. This procedure is much simpler than the other standard methods of factoring and is covered in the final section.
With many algebraic formulas, it is perfectly reasonable to substitute negative numbers for the pronumerals. For example, suppose that I have three bank accounts with balances $A, $B and $C. The total amount $T in the three accounts is given by the formula
![]() T = A + B + C.
T = A + B + C.
The first account is a savings account with a balance of $450, and the second is a term deposit with a balance $2000. The third is a credit card account with a negative balance of −$3000. The total of my three accounts is thus
| T | = A + B + C | |
| = 450 + 2000 − 3000 | ||
| = −550. |
Perhaps the substitution step should have been written as
| T | = A + B + C | |
| = 450 + 2000 + (−3000), |
but once we know about adding and subtracting negative numbers, the working is clearer when we do not worry about such distinctions.
Here are some further examples of substitution. People make different choices about how many middle steps to show − the important thing is to be accurate, particularly with the negative signs.
EXAMPLE
Evaluate each expression for a = 2, b = −5 and c = 3.
| a | a + 3b | b | −3c + 5 | c | 2c − 4b | d | ab − c2 | |||||||
| e | (a − b)(b − c) | f | 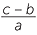 |
g | 2b3 | h | (2b)3 |
Solution
| a | a + 3b | = 2 − 15 | b | −3c + 5 | = −9 + 5 | |||
| = −13 | = −4 |
| c | 2c − 4b | = 6 + 20 | d | ab − c2 | = −10 − 9 | |||
| = 26 | = 19 |
| e | (a − b)(b − c) | = (2 + 5)(−5 − 3) | f | 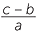 |
= 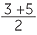 |
|||
| = −56 | = 4 |
| g | 2b3 | = 2 × (−5)3 | h | (2b)3 | = (−10)3 | |||
| = 2 × (−125) | = −1000 | |||||||
| = −250 |
Using fractions in formulas
We can also use positive and negative fractions for pronumerals, as in the following example:
EXAMPLE
If y = x2 −  , find y when:
, find y when:
a![]() x = −1,
x = −1,![]() b
b![]() x =
x = 
![]() c
c![]() x = −
x = −
Solution
| a | When | x | = −1, | b | When | x | =  , , |
c | When | x | = − , , |
|||||
| y | = (−1)2 −  |
y | = 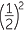 − −  |
y | = 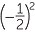 − −  |
|||||||||||
= 1 −  |
=  − −  |
=  − −  |
||||||||||||||
=  |
= 0 | = 0 |
Interpreting negative numbers in formulas
A negative number may involve quantities such as a temperature below zero, or a distance below or south of the point of reference, or money that is owed, or time before some reference time (as in 300BC). For example, the temperature C measured in degrees Celsius is related to the temperature F measure in degrees Fahrenheit by the formula
![]() F =
F = 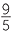 C + 32.
C + 32.
When we substitute C = −5 into this formula, we get
![]() F =
F = 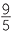 × (−5) + 32 = −9 + 32 = 23
× (−5) + 32 = −9 + 32 = 23
Which means that 5° Celsius below zero is the same as 23° Fahrenheit above zero. On the other hand, substituting C = −20 gives
![]() F =
F =  × (−20) + 32 = −36 + 32 = −4
× (−20) + 32 = −36 + 32 = −4
which means that 20° Celsius below zero is the same as 4° Fahrenheit below zero.
In the example below, negative numbers represent distances below the point
of reference.
EXAMPLE
A stone is thrown vertically upwards at the edge of a lookout with speed V m/s, and its height H metres above the lookout t seconds later is
![]() H = Vt − 5t2 .
H = Vt − 5t2 .
Given that V = 20, find H when:
a ![]() t = 2
t = 2 ![]() b
b![]() t = 4
t = 4 ![]() c
c![]() t = 6
t = 6
What does each result tell you about the position of the stone?
Solution
It is easier if we first substitute V = 20, so that the formula becomes
![]() H = 20t − 5t2 .
H = 20t − 5t2 .
| a | When t = 2, | b | When t = 4, | c | When t = 6, | ||||||||
| H | = 40 − 5 × 4 | H | = 80 − 5 × 16 | H | = 120 − 5 × 36 | ||||||||
| = 20 | = 0 | = −60 | |||||||||||
In part a, the stone has risen 20 metres above the lookout. In part b, the stone has fallen back level with the lookout. In part c, the stone has fallen 60 metres below the lookout.
Like terms
The expression
![]() 5x + 6ab2 − 4x − 10ab2 + t
5x + 6ab2 − 4x − 10ab2 + t
has five terms, which are
![]() 5x, 6ab2, −4x, −10ab2, t.
5x, 6ab2, −4x, −10ab2, t.
Notice that we are saying here that the third term is −4x, not 4x, and that the fourth term is −10ab2, not 10ab2. It usually makes things easier in algebra, particularly when collecting terms, to follow the principle:
- The sign is always part of the term.
(In some later situations, this principle will not be appropriate. For example, when using the difference of squares to factor x2 − 9, the negative sign is best interpreted as ‘minus’.)
Like terms have the same pronumerals, each with the same index.
Thus in the expressions above,
![]() 5x and −4x are like terms and 6ab2 and −10ab2 are like terms.
5x and −4x are like terms and 6ab2 and −10ab2 are like terms.
EXAMPLE
- a
- Identify the individual terms of each expression:
- i
- 3x − 2y + 4z − 6
 ii
ii −5x2 − 12xy2 −
−5x2 − 12xy2 −  xyz2 +
xyz2 +  .
. - b
- Identify the like terms of these expressions (without collecting them):
- i
- 2x − 3 − 4x + 6y − 7
 ii
ii −2x + 2x2 − 3x − 4xy − 5x2
−2x + 2x2 − 3x − 4xy − 5x2
Solution
- a
- i
- The terms are: 3x, −2y, 4z and −6.
- ii
- The terms are: −5x2, −12xy2, −
 xyz2 and
xyz2 and  .
. - b
- i
- The terms 2x and −4x are like terms, and −3 and −7 are like terms.
- ii
- The terms −2x and −3x are like terms, and 2x2 and −5x2 are like terms.
EXERCISE 1
Create a nine-term expression, with no like terms, involving only the pronumerals x and y, and involving no index greater than 2.
Collecting like terms
We can simplify an expression by combining like terms. For example, there are two pairs of like terms in the five-term expression at the start of this section,
![]() 5x + 6ab2 − 4x − 10ab2 + t.
5x + 6ab2 − 4x − 10ab2 + t.
We combine the like terms 5x and −4x to give x. Then we combine the like terms 6ab2 and −10ab2 to give −4ab2. The result is a three−term expression,
![]() 5x + 6ab2 − 4x − 10ab2 + t = x − 4ab2 + t .
5x + 6ab2 − 4x − 10ab2 + t = x − 4ab2 + t .
EXAMPLE
Collect like terms and simplify:
|
a |
3x − 4y − 5x − 6y |
b |
2x2 − 4x + 4x2 − 6x − 6x2 |
|||
|
c |
− |
d |
−x − x2 − x3 − x4 |
Solution
|
a |
3x − 4y − 5x − 6y = −2x − 10y |
b |
2x2 − 4x + 4x2 − 6x − 6x2 = −10x |
|||
|
c |
− |
d |
−x − x2 − x3 − x4 is already simplified. |
EXERCISE 2
Simplify (1 − x2) + (x − x3) + (x2 − x4) + (x3 − x5) + … + (x8 − x10).
When we multiply algebraic expressions, the usual laws of signs for multiplying and dividing numbers apply in exactly the same way:
- The product of two negatives or two positives is positive.
- The product of a positive and a negative is negative.
The following four examples illustrate all the possibilities with the signs:
![]() (6x) × (2x) = 12x2
(6x) × (2x) = 12x2
![]() (−6x) × (2x) = −12x2
(−6x) × (2x) = −12x2
![]() (6x) × (−2x) = −12x2
(6x) × (−2x) = −12x2
![]() (−6x) × (−2x) = 12x2
(−6x) × (−2x) = 12x2
It is useful to have three steps in mind when handling a longer product such as
![]() −2x × (−3a) × 2x × (−3a) = −36a2x2 .
−2x × (−3a) × 2x × (−3a) = −36a2x2 .
- First deal with the signs. Here there are three negatives, so the product is negative.
- Then deal with the numbers. Here 2 × 3 × 2 × 3 = 36.
- Then deal with each pronumeral in turn. Here x × x = x2 and a × a = a2.
EXAMPLE
Simplify each product:
|
a |
(−5a) × (3b) × (−10c) |
b |
(−6t) × (−5t) |
|||
|
c |
(10xy) × (−10xz) |
d |
|
Solution
|
a |
(−5a) × (3b) × (−10c) = 150abc |
b |
(−6t) × (−5t) = 30t2 |
|||
|
c |
(10xy) × (−10xz) = −100x2yz |
d |
|
Powers of negatives
Squares, cubes and higher powers of a negative can be evaluated at this stage by regarding them as repeated products:
![]() (−3a)2 = (−3a) × (−3a) = 9a2
(−3a)2 = (−3a) × (−3a) = 9a2
![]() (−3a)3 = (−3a) × (−3a) × (−3a) = −27a3
(−3a)3 = (−3a) × (−3a) × (−3a) = −27a3
![]() (−3a)4 = (−3a) × (−3a) × (−3a) × (−3a) = 81a4
(−3a)4 = (−3a) × (−3a) × (−3a) × (−3a) = 81a4
Such calculations will become quicker and more systematic later in this module, when we begin to integrate the index laws into algebra.
EXAMPLE
Simplify:
a![]() (−4y)2
(−4y)2 ![]() b
b![]()
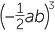
![]() c
c![]() (−3st)4
(−3st)4
Solution
| a | (−4y)2 | = (−4y) × (−4y) | b | 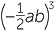 |
=  × ×  × ×  |
||
| = 16y2 | = −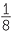 a3b3 a3b3 |
||||||
| c | (−3st)4 | = (−3st) × (−3st) × (−3st) × (−3st) | |||||
| = 81s4t4 | |||||||
We have already seen the distributive law at work in arithmetic. The quick methods of calculation below relied on expanding brackets.
| 7 × 21 | = 7 × (20 + 1) | |
| = 7 × 20 + 7 × 1 | ||
| = 140 + 7 | ||
| = 147 | ||
| and | ||
| 12 × 49 | = 12 × (50 − 1) | |
| = 12 × 50 − 12 × 1 | ||
| = 600 − 12 | ||
| = 588 | ||
Exactly the same procedures apply in algebra, because the pronumerals represent numbers. We expanded brackets before in the module, Algebraic Expressions, but the issue now is dealing with minus signs:
![]() 5x(x − 3) = 5x2 − 15x −4(2x − 7) = −8x + 28 −3a(−5 + 2b) = 15a − 6ab.
5x(x − 3) = 5x2 − 15x −4(2x − 7) = −8x + 28 −3a(−5 + 2b) = 15a − 6ab.
The important principle here is to include the sign with the factor outside the bracket:
- The sign is part of the factor.
Thus the factors on the left in the three expressions are
![]() 5x and −4 and −3a.
5x and −4 and −3a.
Each product is calculated using the methods of the previous section. Don’t take short cuts with these products − work systematically with the signs, then with the numbers, then with each pronumeral in turn.
EXAMPLE
Expand the brackets in each expression:
| a | −4(x − 4) | b | −5y(−5y + 1) | |||
| c | −3a(7b + 8) | d | 5xy(x − y + z) |
Solution
| a | −4(x − 4) = −4x + 16 | b | −5y(−5y + 1) = 25y2 − 5y | |||
| c | −3a(7b + 8) = −21ab − 24a | d | 5xy(x −y + z) = 5x2y − 5xy2 + 5xyz |
Collecting like terms after expanding brackets
In longer expressions, it is sometimes possible to collect like terms once the brackets have been expanded. For example,
| 3 − 4(x − 5) | = 3 − 4x + 20 | Care: (-4) × (-5) = 20 | |
| = 23 − 4x |
EXAMPLE
Expand the brackets in each expression, then collect like terms.
| a | −5x(6 − x) − x2 | b | x2 − x − 5(x − 2) | |||
| c | 2(x − 5) − 5(x − 2) | d | −10(x2 − x) + 6x(2x − 3) |
Solution
| a | −5x(6 − x) − x2 | = −30x + 5x2 − x2 | b | x2 − x − 5(x − 2) | = x2 − x − 5x + 10 | |||
| = −30x + 4x2 | = x2 − 6x + 10 |
| c | 2(x − 5) − 5(x − 2) | = 2x − 10 − 5x + 10 | |
| = −3x |
| d | −10(x2 − x) + 6x(2x − 3) | = −10x2 + 10x + 12x2 − 18x | |
| = 2x2 − 8x |
The three index laws for products and powers
A product such as x3 × x2 can always be evaluated as x × x × x × x × x = x5, and such intuitions can be lost if the index laws are introduced too early into algebra. Such computations are clumsy, however, and when students are ready for them, the index
laws make things much simpler.
Substitution into expressions involving powers
Before discussing the index laws, a point of notation needs to be reviewed.
5x3 means 5 × x3 = 5 × x × x × x and (5x)3 means 5x × 5x × 5x.
The interpretation of 5x3 as 5 × x3 follows from our conventions for the order
of operations:
- In the absence of brackets, powers are evaluated before products.
Thus the notation 5x3 means that x3 is first evaluated, then the result is multiplied by 5.
EXAMPLE
When x = −2 and a = −10, evaluate:
a![]() 5x3
5x3 ![]() b
b![]() (5x)3
(5x)3![]() c
c![]() (ax)2
(ax)2 ![]() d
d![]() ax2
ax2
Solution
| a | 5x3 | = 5 × (−2)3 | |
| = 5 × (−8) | |||
| = −40 | |||
| b | (5x)3 | = (5 × (−2))3 | |
| = (−10)3 | |||
| = −1000 | |||
| c | (ax)2 | = ((−10) × (−2))2 | |
| = 202 | |||
| = 400 | |||
| d | ax2 | = −10 × (−2)2 | |
| = −10 × 4 | |||
| = −40 |
The index laws for products and powers
The index laws were introduced for whole numbers in the module Multiples, Factors and Powers. In this module, we will be applying to algebra the three index laws that do not involve fractions or division.
First, we saw before that when multiplying powers of the same base, we add the indices. For example, 52 × 54 = 56, because
![]() 52 × 54 = (5 × 5) × (5 × 5 × 5 × 5) = 56.
52 × 54 = (5 × 5) × (5 × 5 × 5 × 5) = 56.
Secondly, we saw that when raising a power to a power, we multiply the indices.
For example, (64)3 = 612, because using the previous law,
![]() (64)3 = 64 × 64 × 64 = 612.
(64)3 = 64 × 64 × 64 = 612.
Thirdly, we saw that the power of a product is the product of the powers. For example,
×5)3 = 23 × 53, because using the any-order property of multiplication,
![]() (2 × 5)3 = (2 × 5) × (2 × 5) × (2 × 5) = 23 × 53.
(2 × 5)3 = (2 × 5) × (2 × 5) × (2 × 5) = 23 × 53.
Because pronumerals represent numbers, these index laws apply in exactly the same way in algebra. Expressed in algebraic notation, the three laws become
- When multiplying powers of the same base, add the indices,
![]() am × an = am + n, where a is any number, and m and n are nonzero whole numbers.
am × an = am + n, where a is any number, and m and n are nonzero whole numbers.
Justifying this by an example, a2 × a4 = (a × a) × (a × a × a × a) = a6.
- When raising a power to a power, multiply the indices,
![]() (am)n = amn, where a is any number, and m and n are nonzero whole numbers.
(am)n = amn, where a is any number, and m and n are nonzero whole numbers.
Justifying this by an example, (a4)3 = a4 × a4 × a4 = a12.
- The power of a product is the product of the powers,
![]() (a × b)n = an × bn, where a and b are any numbers, and n is a nonzero whole number.
(a × b)n = an × bn, where a and b are any numbers, and n is a nonzero whole number.
Justifying this by an example, (a × b)3 = (a × b) × (a × b) × (a × b) = a3 × b3.
In the module, Indices and Logarithms we will explain how to extend these laws so that the indices m and n can also be negative or fractional. At this stage, however, such powers have not even been defined, and the pronumerals m and n are therefore restricted to the nonzero whole numbers.
Multiplying algebraic expressions
We will now apply these three index laws in various situations. The law am × an = am + n arises when we multiply. For example,
![]() 3x6 × 5x10 = 15x16
3x6 × 5x10 = 15x16 ![]() and
and ![]() (2y5z) × (−5y3z) = −10y8z2 .
(2y5z) × (−5y3z) = −10y8z2 .
The second of these examples demands a systematic approach:
- First deal with the signs. Here the product of a positive and a negative is a negative.
- Then deal with the numbers. Here the product of 2 and 5 is 10.
- Then deal with each pronumeral in turn. Here y5 × y3 = y8 and z × z = z2.
EXAMPLE
Use the index laws, and the rules for signs, to simplify:
| a | 3x4 × 4x3 | b | 5x2 × (−2x3) × (−3x4) | |||
| c | (−a3b3c3) × abc | d |  r5s3 × r5s3 × 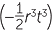 |
Solution
| a | 3x4 × 4x3 = 12x7 | b | 5x2 × (−2x3) × (−3x4) = 30x9 | |||
| c | (−a3b3c3) × abc = −a4b4c4 | d |  r5s3 × r5s3 × 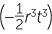 = − = − r8s3t3 r8s3t3 |
Taking the power of a product
The law (ab)n = anbn arises when we take a power of a product. For example,
![]() (−2x)3 = −23 × x3 = −8x3 and (−10abc)4 = 104 × a4b4c4 = 10 000a4b4c4.
(−2x)3 = −23 × x3 = −8x3 and (−10abc)4 = 104 × a4b4c4 = 10 000a4b4c4.
These examples show that the same systematic approach is needed with powers. Deal first with the sign, then with the numbers, then with each pronumeral in turn. The product of two negatives is a positive, so the sign of a power of a negative depends on whether the index is even or odd:
- An even power of a negative is positive, and an odd power of a negative is odd.
For example,
![]() (-x)6 = x6 and (-x)7 = -x7 .
(-x)6 = x6 and (-x)7 = -x7 .
EXAMPLE
Simplify:
| a | (−4y)2 | b | (−3ab)3 | c | 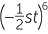 |
|||||
|
Solution |
||||||||||
| a | (−4y)2 = 16y2 | b | (−3ab)3 = −27a3b3 | c |  = = 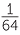 s6t6 s6t6 |
|||||
We can combine the two laws discussed so far, as in the following example.
EXAMPLE
Use the index laws, and the rules for signs, to simplify:
| a | (3a)2 × (−2a)3 | b | (5ab)2 × (−2ac)2 | ||||||
| c | (−abc)10 × (ac)5 | d | (2r)4 × (−5r)4 × −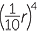 |
||||||
|
Solution |
|||||||||
| a | (3a)2 × (−2a)3 | = 9a2 × (−8a3) | b | (5ab)2 × (−2ac)2 | = 25a2b2 × 4a2c2 | ||||
| = −72a5 | = 100a4b2c2 | ||||||||
| c | (−abc)10 × (ac)5 | = a10b10c10 × a5c5 | d | (2r)4 × (−5r)4 × −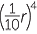 |
= 24r4 × 54r4 × 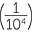 r4 r4 |
||||
| = a15b10c15 | = r12 | ||||||||
Taking the power of a power
The law (am)n = amn applies when we take a power of an expression involving indices.
For example,
| (2x4)3 | = 23 × (x4)3 | (−3a5b5)3 | = −33 × (a5)3 × (b5)3 | ||
| = 8x12 | = −27a15b15 |
The following examples use all three laws.
EXAMPLE
Use the index laws to simplify:
| a | (4a4)2 | b | (−5a2)2 × (−2a3) | |||
| c | (−a3b3c3)3 | d | (12r2)2 × (2r2)2 |
Solution
| a | (4a4)2 | = 16a8 | b | (−5a2)2 × (−2a3) | = 25a4 × (−2a3) | ||||||||
| = −50a7 | |||||||||||||
| c | (−a3b3c3)3 | = −a9b9c9 | b | (12r2)2 × (2r2)2 | = 144r4 × 4r4 | ||||||||
| = 576r8 | |||||||||||||
The next examples show that it may be possible to collect like terms after applying the index laws.
EXAMPLE
Expand each power or product, then collect like terms.
a![]() (2x3)2 − (2x2)3
(2x3)2 − (2x2)3 ![]() b
b![]() (3a3) × (4a4) − (2a2) × (-5a5)
(3a3) × (4a4) − (2a2) × (-5a5)
Solution
| a | (2x3)2 − (2x2)3 | = 4x6 − 8x6 | b | (3a3) × (4a4) − (2a2) × (−5a5) | = 12a7 + 10a7 | |||
| = −4x6 | = 22a7 |
EXERCISE 3
a![]() Simplify (−xy)20 + (−x)20(−y)20
Simplify (−xy)20 + (−x)20(−y)20 ![]() b
b![]() Simplify (−xy)21 + (−x)21(−y)21
Simplify (−xy)21 + (−x)21(−y)21
EXERCISE 4
If (ax4)3 = (8x3)4, find the value of a.
The remaining two index laws
For reference, the remaining two index laws are stated here. They will be discussed in the module, Special Expansions in Algebraic Fractions once division and algebraic fractions have been introduced.
- When dividing powers of the same base, subtract the indices.
For any non-zero number a and nonzero whole numbers m ≠ n,
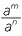 = am − n when m > n.
= am − n when m > n. 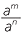 =
= 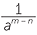 when m < n.
when m < n.
- The power of a quotient is the quotient of the powers.
For any numbers a and b, where b ≠ 0, and any nonzero whole number n,
 =
= 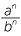 , where a and b are any numbers, and n is a non zero whole number.
, where a and b are any numbers, and n is a non zero whole number.
The index laws and the distributive law
Expanding brackets using the distributive law often involves the index laws. For example,
3x2(4x − x2) = 12x3 − 3x4 ![]() and
and![]() −2a6(a2 − a4) = −2a8 + 2a10.
−2a6(a2 − a4) = −2a8 + 2a10.
EXAMPLE
Expand the brackets in each expression:
| a | a6(a7 − a8) | b | −3a2(1 − a − 13a2) | |||
|
Solution |
||||||
| a | a6(a7 − a8) = a13 − a14 | b | −3a2(1 − a − 13a2) = −3a2 + 3a3 + 39a4 | |||
Collecting like terms after expanding brackets
As we have seen before, it may be possible to collect like terms after brackets have been expanded. For example,
| 3x2(x − x3) − 2x3(1 − x2) | = 3x3 − 3x5 − 2x3 + 2x5 | |
| = x3 − x5 |
EXAMPLE
Expand the brackets, then collect like terms:
a![]() a4(x − a3) − a3(x − a4)
a4(x − a3) − a3(x − a4)
b![]() x3(x2 − 1) + x2(x3 − 1)
x3(x2 − 1) + x2(x3 − 1)
Solution
| a | a4(x − a3) − a3(x − a4) | = a4x − a7 − a3x + a7 | |
| = a4x − a3x |
| b | x3(x2 − 1) + x2(x3 − 1) | = x5 − x3 + x5 − x2 | |
| = 2x5 − x3 − x2 |
EXERCISE 5
Simplify x(1 − x) + x(x − x2) + x(x2 − x3) + x(x3 − x4) + … + x(x11 − x12)
Factoring an expression by taking out the HCF
The process of expanding brackets by the distributive law can be reversed by what is known as ‘taking out’ a common factor from all the terms. For example, we can write 3x + 6 as
![]() 3x + 6 = 3(x + 2).
3x + 6 = 3(x + 2).
The terms 3x and 6 have common factor 3. We place this 3 out in front of the brackets, and then place the other factor of each term inside the brackets. Always check your answer by expanding.
When we try to factor 5abc − 15ab, there are many common factors that we could take out, but the most complete factoring is obtained by taking out the highest common factor 5ab,
![]() 5abc − 15ab = 5ab(c − 3) .
5abc − 15ab = 5ab(c − 3) .
This procedure is therefore called factoring an expression by taking out the HCF.
In the expression ab + abx − aby, the first term ab is a divisor of the other two terms.
The first term is therefore the HCF of all the terms, and factoring results in a 1 inside
the bracket,
![]() ab + abx − aby = ab(1 + x − y) .
ab + abx − aby = ab(1 + x − y) .
There are three steps in the procedure.
- Find the HCF of all the terms.
- Place the HCF outside the brackets, and place the other factor of each term inside.
- Check your factoring by expanding the brackets.
In the module, Factorisation we will sometimes need to take the HCF in the example above as −ab, and factor it as
![]() ab + abx − aby = −ab(−1 − x + y) .
ab + abx − aby = −ab(−1 − x + y) .
but at this stage, using an HCF with a negative is only a curiosity.
EXAMPLE
Factor each expression by taking out the HCF:
| a | 3x + 6y + 9z | b | x2 − 5x | |||
| c | 4ab − 6bc | d | x − 2xy + xy2 | |||
|
Solution |
||||||
| a | 3x + 6y + 9z = 3(x + 2y + 3z) | b | x2 − 5x = x(x − 5) | |||
| c | 4ab − 6bc = 2b(2a − 3c) | d | x − 2xy + xy2 = x(1 − 2y + y2) | |||
Using the index laws to take out the HCF
When higher indices are involved, the index laws are needed. For example,
![]() x8 − 2x7 + x6 = x6(x2 − 2x + 1) .
x8 − 2x7 + x6 = x6(x2 − 2x + 1) .
Here x6 is the HCF of the terms x8, −2x7 and x6 − we take the power with the lowest index.
When several pronumerals are involved, we need to take the lowest index of the powers of each pronumeral in turn. For example,
![]() 2a4b4c4 − 4a3b4c5 = 2a3b4c4(a − 2c).
2a4b4c4 − 4a3b4c5 = 2a3b4c4(a − 2c).
EXAMPLE
Factor each expression:
| a | x3 + x6 − x9 | b | 10a8b6 − 25a6b8 | |||
|
Solution |
||||||
| a | x3 + x6 − x9 = x3(1 + x3 − x6) | b | 10a8b6 − 25a6b8 = 5a6b6(2a2 − 5b2) | |||
Taking out the HCF in mental arithmetic
Sometimes additions and subtractions in mental arithmetic are naturally suited to the approach of taking out a common factor, as in the following example:
EXAMPLE
Show how taking out the HCF is used to perform the following examples mentally:
| a | 300 + 600 + 800 | b | 33 + 88 + 55 | |||||
|
Solution |
||||||||
| a | 300 + 600 + 800 | = 100(3 + 6 + 8) | b | 33 + 88 + 55 | = 11(3 + 8 + 5) | |||
| = 100 × 17 | = 11 × 16 | |||||||
Mental arithmetic is very much a matter of taste. Some people instinctively perform the following additions by recognising the common factors 12 and 7. Others regard the use of a common factor in such situations as a distraction.
| 132 − 36 − 48 | = 12(11 − 3 − 4) | 14 + 84 + 63 − 21 | = 7(2 + 12 + 9 + 3) | ||
| = 12 × 4 | = 7 × 20 | ||||
| = 48 | = 140 |
As mentioned in the Motivation section, this module is the second of four modules dealing with basic manipulation of algebraic expressions. The four modules are:
- Algebraic Expressions
- Negatives and the Index Laws in Algebra (the present module)
- Fractions and the Index Laws in Algebra
- Special Expansions and Algebraic Fractions
This module has now covered algebraic expressions with negatives, providing all the skills for solving the straightforward linear equations that are discussed in the module, Linear Equations. In particular, distracting constraints about ‘keeping the coefficient of x positive’ will be unnecessary. For example, both solutions below of the given equation are well motivated − in the first, all the terms in x are moved to the left, in the second, the terms in x are moved to the right to avoid negatives:
| 3x − 6 | = 5x − 12 | 3x − 6 | = 5x − 12 | |||
  |
−2x | = −6 |   |
6 | = 2x | |
 |
x | = 3 |  |
x | = 3 |
Students should have the skills to carry out both procedures, and then decide which approach they may prefer in a particular equation.
The three index laws introduced into algebra in this module concern products, rather than quotients or fractions. As discussed in the text above, the remaining two index laws will be introduced in the context of fractions and algebra in the third module, Fractions and the Index Laws in Algebra.
This third module also formally introduces rational numbers. Although simple negative fractions are used freely before this, there needs to be a systematic treatment of them. This allows algebraic fractions to be introduced, but they are only dealt with systematically in the fourth module, Special Expansions and Algebraic Fractions.
Factoring by taking out the HCF is, as mentioned in the Motivation section, only the first step in the study of factoring, which is the focus of attention of a large part of secondary school algebra. The next step in factoring comes when one tried to reverse the expansion of two sets of brackets,
![]() (x + 3)(x + 5) = x2 + 8x + 15
(x + 3)(x + 5) = x2 + 8x + 15
and to reverse the use of the three special expansions
![]() (x + a)2 = x2 + 2ax + a2
(x + a)2 = x2 + 2ax + a2
![]() (x − a)2 = x2 − 2ax + a2
(x − a)2 = x2 − 2ax + a2
![]() (x − a)(x + a) = x2 − a2 .
(x − a)(x + a) = x2 − a2 .
Expanding two sets of brackets, and the three special expansions, are dealt within the fourth module, Special Expansions and Algebraic Fractions. Reversing these procedures will then be discussed in modules appropriate for Years 9−10.
EXERCISE 1
An example of such an expression is 1 + x + x2 + y + y2 + xy + x2y + xy2 + x2y2.
EXERCISE 2
1 + x − x9 − x10
EXERCISE 3
| a | (−xy)20 + (−x)20(−y)20 | = x20y20 + x20y20 | b | (−xy)21 + (−x)21(−y)21 | = −x21y21 + x21y21 | |||
| = 2x20y20 | = 0 |
EXERCISE 4
Expanding the brackets, and using the fact that 8 = 23,
| RHS | = (23 × x3)4 | ||
| = 212 × x12 | |||
| and | LHS | = a3 × x12 | |
| Hence | a3 | = 212 | |
| a | = 24 | ||
| = 16. |
EXERCISE 5
![]() x(1 − x) + x(x − x2) + x(x2 − x3) + x(x3 − x4) + … + x(x11 − x12)
x(1 − x) + x(x − x2) + x(x2 − x3) + x(x3 − x4) + … + x(x11 − x12)
![]() = x − x2 + x2 − x3 + x3 − x4 + x4 − x5 + … + x12 − x13
= x − x2 + x2 − x3 + x3 − x4 + x4 − x5 + … + x12 − x13
![]() = x − x13
= x − x13
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()