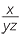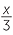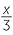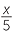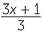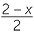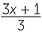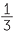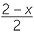The Improving Mathematics Education in Schools (TIMES) Project
- Fluency with addition, subtraction, multiplication and division of whole numbers
and fractions. - Ability to apply the any-order principle for multiplication and addition (commutative law and associative law) for whole numbers and fractions.
- Familiarity with the order of operation conventions for whole numbers.
Algebra is a fascinating and essential part of mathematics. It provides the written language in which mathematical ideas are described.
Many parts of mathematics are initiated by finding patterns and relating to different quantities. Before the introduction and development of algebra, these patterns and relationships had to be expressed in words. As these patterns and relationships became more complicated, their verbal descriptions became harder and harder to understand. Our modern algebraic notation greatly simplifies this task.
A well-known formula, due to Einstein, states that E = mc2. This remarkable formula gives the relationship between energy, represented by the letter E, and mass, represented by letter m. The letter c represents the speed of light, a constant, which is about 300 000 000 metres per second. The simple algebraic statement E = mc2 states that some matter is converted into energy (such as happens in a nuclear reaction), then the amount of energy produced is equal to the mass of the matter multiplied by the square of the speed of light. You can see how compact the formula is compared with the verbal description.
We know from arithmetic that 3 × 6 + 2 × 6 = 5 × 6. We could replace the number 6 in this statement by any other number we like and so we could write down infinitely many such statements. All of these can be captured by the algebraic statement 3x + 2x = 5x, for any number x. Thus algebra enables us to write down general statements clearly and concisely.
The development of mathematics was significantly restricted before the 17th century by the lack of efficient algebraic language and symbolism. How this notation evolved will be discussed in the History section.
In algebra we are doing arithmetic with just one new feature − we use letters to represent numbers. Because the letters are simply stand-ins for numbers, arithmetic is carried out exactly as it is with numbers. In particular the laws of arithmetic (commutative, associative and distributive) hold.
For example, the identities
| 2 + x = x + 2 | 2 × x = x × 2 | ||
| (2 + x) + y = 2 + (x + y) | (2 × x) × y = 2 × (x × y) | ||
| 6(3x + 1) = 18x + 6 |
hold when x and y are any numbers at all.
In this module we will use the word pronumeral for the letters used in algebra. We choose to use this word in school mathematics because of confusion that can arise from the words such as ‘variable’. For example, in the formula E = mc2, the pronumerals E and m are variables whereas c is a constant.
Pronumerals are used in many different ways. For example:
- Substitution: ‘Find the value of 2x + 3 if x = 4.’ In this case the pronumeral is given the value 4.
- Solving an equation: ‘Find x if 2x + 3 = 8.’ Here we are seeking the value of the pronumeral that makes the sentence true.
- Identity: ‘The statement of the commutative law: a + b = b + a.’ Here a and b can be any real numbers.
- Formula: ‘The area of a rectangle is A = lw.‘ Here the values of the pronumerals are connected by the formula.
- Equation of a line or curve: ‘The general equation of the straight line is y = mx + c.’
Here m and c are parameters. That is, for a particular straight line, m and c are fixed.
In some languages other than English, one distinguishes between ‘variables’ in functions and ‘unknown quantities’ in equations (‘incógnita’ in Portuguese/Spanish, ‘inconnue’ in French) but this does not completely clarify the situation. The terms such as variable and parameter cannot be precisely defined at this stage and are best left to be introduced later in the development of algebra.
An algebraic expression is an expression involving numbers, parentheses, operation signs and pronumerals that becomes a number when numbers are substituted for the pronumerals. For example 2x + 5 is an expression but +) × is not.
Examples of algebraic expressions are:
![]() 3x + 1 and 5(x2 + 3x)
3x + 1 and 5(x2 + 3x)
As discussed later in this module the multiplication sign is omitted between letters and between a number and a letter. Thus substituting x = 2 gives
![]() 3x + 1 = 3 × 2 + 1 = 7
3x + 1 = 3 × 2 + 1 = 7 ![]() and
and ![]() 5(x2 + 3x) = 5(22 + 3 × 2) = 30.
5(x2 + 3x) = 5(22 + 3 × 2) = 30.
In this module, the emphasis is on expressions, and on the connection to the arithmetic that students have already met with whole numbers and fractions. The values of the pronumerals will therefore be restricted to the whole numbers and non-negative fractions.
Changing words to algebra
In algebra, pronumerals are used to stand for numbers. For example, if a box contains x stones and you put in five more stones, then there are x + 5 stones in the box. You may or may not know what the value of x is (although in this example we do know that x is a whole number).
- Joe has a pencil case that contains an unknown number of pencils. He has three
other pencils. Let x be the number of pencils in the pencil case. Then Joe has x + 3 pencils altogether.
![]()
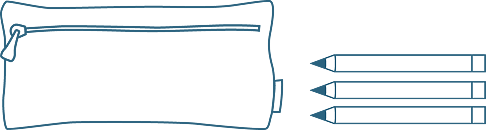
- Theresa has a box with least 5 pencils in it, and 5 are removed. We do not know how many pencils there are in the pencil case, so let z be the number of pencils in the box. Then there are z − 5 pencils left in the box.
 There are three boxes, each containing
x marbles in each box, then the total number of marbles is 3 × x = 3x.
There are three boxes, each containing
x marbles in each box, then the total number of marbles is 3 × x = 3x. - If n oranges are to be divided amongst 5 people, then each person receives
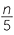 oranges. (Here we assume that n is a whole number. If each person is to get a whole number of oranges, then n must be a multiple of 5.)
oranges. (Here we assume that n is a whole number. If each person is to get a whole number of oranges, then n must be a multiple of 5.)
The following table gives us some meanings of some commonly occurring
algebraic expressions.
| x + 3 |
|
| x − 3 |
|
| 3 × x |
|
| x ÷ 3 |
|
| 2 × x − 3 |
|
| x ÷ 3 + 2 |
|
Expressions with zeroes and ones
Zeroes and ones can often be eliminated entirely. For example:
![]() x + 0 = x
x + 0 = x![]() (Adding zero does not change the number.)
(Adding zero does not change the number.)
![]() 1 × x = x
1 × x = x![]() (Multiplying by one does not change the number.)
(Multiplying by one does not change the number.)
Algebraic notation
In algebra there are conventional ways of writing multiplication, division and indices.
Notation for multiplication
The × sign between two pronumerals or between a pronumeral and a number is usually omitted. For example, 3 × x is written as 3x and a × b is written as ab. We have been following this convention earlier in this module.
It is conventional to write the number first. That is, the expression 3 × a is written as 3a and not as a3.
Notation for division
The division sign ÷ is rarely used in algebra. Instead the alternative fraction notation for division is used. We recall 24 ÷ 6 can be written as 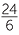 . Using this notation, x divided by 5
. Using this notation, x divided by 5
is written as 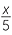 , not as x ÷ 5.
, not as x ÷ 5.
Index notation
x × x is written as x2 and y × y × y is written as y3.
EXAMPLE
Write each of the following using concise algebraic notation.
- a
- A number x is multiplied by itself and then doubled.
- b
- A number x is squared and then multiplied by the square of a second number y.
- c
- A number x is multiplied by a number y and the result is squared.
Solution
a![]() x × x × 2 = x2 × 2 = 2x2.
x × x × 2 = x2 × 2 = 2x2. ![]() b
b![]() x2 × y2 = x2y2.
x2 × y2 = x2y2.
c![]() (x × y)2 = (xy)2 which is equal to x2y2
(x × y)2 = (xy)2 which is equal to x2y2
Summary
|
|
Assigning values to a pronumeral is called substitution.
EXAMPLE
If x = 4, what is the value of:
a ![]() 5x
5x ![]() b
b ![]() x + 3
x + 3 ![]() c
c![]() x − 1
x − 1 ![]() d
d![]()

Solution
a![]() 5x = 5 × 4 = 20
5x = 5 × 4 = 20 ![]() b
b![]() x + 3 = 4 + 3 = 7
x + 3 = 4 + 3 = 7![]() c
c![]() x − 1 = 4 − 1 = 3
x − 1 = 4 − 1 = 3![]() d
d![]()
 =
= 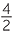 = 2
= 2
EXAMPLE
If x = 6, what is the value of:
|
a |
3x + 4 |
b |
2x + 3 |
c |
2x − 5 |
|||||
|
d |
|
e |
|
Solution
|
a |
3x + 4 = 3 × 6 + 4 = 22 |
b |
2x + 3 = 2 × 6 + 3 = 15 |
|||
|
c |
2x − 5 = 2 × 6 − 5 = 7 |
d |
|
|||
|
e |
|
Adding and subtracting like terms
Like terms
If you have 3 pencil case with the same number x of pencils in each, you have 3x pencils altogether.
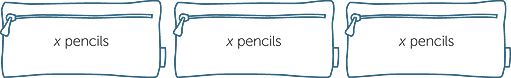
If there are 2 more pencil cases with x pencils in each, then you have 3x + 2x = 5x pencils altogether. This can be done as the number of pencils in each case is the same. The terms 3x and 2x are said to be like terms.
Consider another example. If Jane has x packets of chocolates each containing y chocolates, then she has x × y = xy chocolates.
If David has twice as many chocolates as Jane, he has 2 × xy = 2xy chocolates.
Together they have 2xy + xy = 3xy chocolates.
The terms 2xy and xy are like terms. Two terms are called like terms if they involve exactly the same pronumerals and each pronumeral has the same index.
EXAMPLE
Which of the following pairs consists of like terms:
a![]() 3x, 5x
3x, 5x ![]() b
b![]() 4x2, 8x
4x2, 8x ![]() c
c![]() 4x2y, 12x2y
4x2y, 12x2y
Solution
- a
- 5x and 3x are like terms.
- b
- 4x2 and 8x are not like terms since the powers of x are different.
- c
- 4x2y, 12x2y are like terms
Adding and subtracting like terms
The distributive law explains the addition and subtraction of like terms. For example:
![]() 2xy + xy = 2 × xy + 1 × xy =(2 + 1)xy = 3xy
2xy + xy = 2 × xy + 1 × xy =(2 + 1)xy = 3xy
The terms 2x and 3y are not like terms because the pronumerals are different. The terms 3x and 3x2 are not like terms because the indices are different. For the sum 6x + 2y + 3x, the terms 6x and 3x are like terms and can be added. There are no like terms for 2y, so by using the commutative law for addition the sum is
![]() 6x + 2y + 3x = 6x + 3x + 2y = 9x + 2y.
6x + 2y + 3x = 6x + 3x + 2y = 9x + 2y.
The any-order principle for addition is used for the adding like terms.
Because of the commutative law and the associative law for multiplication (any-order principle for multiplication) the order of the factors in each term does not matter.
![]() 5x × 3y = 15xy = 15yx
5x × 3y = 15xy = 15yx
![]() 6ab × 3b2a = 18a2b3 = 18b3a2
6ab × 3b2a = 18a2b3 = 18b3a2
Like terms can be added and subtracted as shown in the example below.
EXAMPLE
Simplify each of the following by adding or subtracting like terms:
| a | 2x + 3x + 5x | b | 3xy + 2xy | c | 4x2 − 3x2 | |||||
| d | 2x2 + 3x + 4x | e | 4x2y − 3x2y + 3xy2 |
Solution
| a | 2x + 3x + 5x = 10x | b | 3xy + 2xy = 5xy | |||
| c | 4x2 − 3x2 = x2 | d | 2x2 + 3x + 4x = 2x2 + 7x | |||
| e | 4x2y − 3x2y + 3xy2 = x2y + 3xy2 |
Brackets fulfill the same role in algebra as they do in arithmetic. Brackets are used in algebra in the following way.
![]() ‘Six is added to a number and the result is multiplied by 3.’
‘Six is added to a number and the result is multiplied by 3.’
Let x be the number. Then the expression is (x + 6) × 3. We now follow the convention that the number is written at the front of the expression (x + 6) without a multiplication sign. The preferred form is thus 3(x + 6).
EXAMPLE
For a party, the host prepared 6 tins of chocolate balls, each containing n chocolate balls.

- a
- The host places two more chocolates in each tin. How many chocolates are there altogether in the tins now?
- b
- If n = 12, that is, if there were originally 12 chocolates in each box, how many chocolates are there altogether in the tins now?
Solution
- a
- The number of chocolates in each tin is now n + 2. There are 6 tins, and therefore there are 6 (n + 2) chocolates in total.
- b
- If n = 12, the total number of chocolates is 6 (n + 2) = 6 (12 + 2) = 6 × 14 = 84.
EXERCISE 1
Each crate of bananas contains n bananas. Three bananas are removed from each crate.
- a
- How many bananas are now in each crate?
- b
- If there are 7 crates, how many bananas are there now in total?
EXERCISE 2
Five extra seats are added to each row of seats in a theatre. There were s seats in each row and there are 20 rows of seats. How many seats are there now in total?
Use of brackets and powers
The following example shows the importance of following the conventions of order of operations when working with powers and brackets.
- 2x2 means 2 × x2
- (2x)2 = 2x × 2x = 4x2
EXAMPLE
For x = 3, evaluate each of the following:
a
![]() 2x2
2x2
![]() b
b
![]() (2x)2
(2x)2
Solution
a![]() 2x2 = 2 × x × x = 2 × 3 × 3 = 18
2x2 = 2 × x × x = 2 × 3 × 3 = 18
![]() b
b![]() (2x)2 = (2 × x)2 = (2 × 3)2 = 36
(2x)2 = (2 × x)2 = (2 × 3)2 = 36
EXERCISE 3
Evaluate each expression for x = 3.
a![]() 10x3
10x3 ![]() b
b![]() (10x)3
(10x)3
Multiplying algebraic terms involves the any-order property of multiplication discussed for whole numbers.
The following shows how the any-order property can be used
| 3x × 2y × 2xy | = 3 × x × 2 × y × 2 × x × y |
| = 3 × 2 × 2 × x × x × y × y | |
| = 12x2y2 |
EXAMPLE
Simplify each of the following:
a![]() 5 × 2a
5 × 2a ![]() b
b![]() 3a × 2a
3a × 2a ![]() c
c![]() 5xy × 2xy
5xy × 2xy
Solution
- a
- 5 × 2a = 10a
- b
- 3a × 2a = 3 × a × 2 × a = 6a2
- c
- 5xy × 2xy = 5 × x × y × 2 × x × y = 10x2y2
With practice no middle steps are necessary.
For example, 2a × 3a × 2a2 = 12a4
Arrays of dots have been used to represent products in the module, Multiplication of Whole Numbers.
For example 2 × 6 = 12 can be represented by 2 rows of 6 dots.
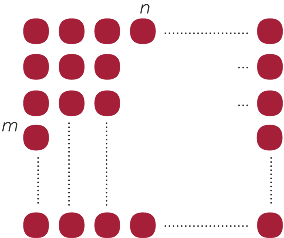
The diagram below represents two rows with some number of dots.

Let n be the number of dots in each row. Then there are 2 × n = 2n dots.
If an array is m dots by n dots then there are mn dots. If the array is m × n then by convention we have m rows and n columns. We can represent the product m × n = mn by such an array.
EXAMPLE

The pattern goes on forever.
How many dots are there in the nth diagram?
Solution
In the 1st diagram there are 1 × 1 = 12 dots.
In the 2nd diagram there are 2 × 2 = 22 dots.
In the 3rd diagram there are 3 × 3 = 32 dots.
In the nth diagram there will be n × n = n2 dots.
Areas
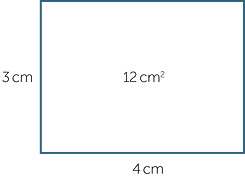 We can also represent a product like 3 × 4 by a rectangle.
We can also represent a product like 3 × 4 by a rectangle.
![]() The area of a 3 cm by 4 cm rectangle is 12 cm2.
The area of a 3 cm by 4 cm rectangle is 12 cm2.
 The area of a x cm by y cm rectangle is x × y = xy cm2.
The area of a x cm by y cm rectangle is x × y = xy cm2.
(x and y can be any positive numbers.)
 The area of a x cm by x cm square is x2 cm2.
The area of a x cm by x cm square is x2 cm2.
(x can be any positive number.)
EXAMPLE
Find the total area of the two rectangles in terms of x and y.

Solution
The area of the rectangle to the left is xy cm2 and the area of the rectangle to the right is 2xy cm2. Hence the total area is xy + 2xy = 3xy cm2.
Some simple statements with numbers demonstrate the convenience of algebra.
EXAMPLE
The nth positive even number is 2n.
- a
- What is the square of the nth positive even number?
- b
- If the nth positive even number is doubled what is the result?
Solution
- a
- The square of the nth positive even number is (2n)2 = 4n2
- b
- The double of the nth positive even number is 2 × 2n = 4n.
EXERCISE 4
a![]() If b is even, what is the next even number?
If b is even, what is the next even number?
b![]() If a is a multiple of three, what are the next two multiples of 3?
If a is a multiple of three, what are the next two multiples of 3?
c![]() If n is odd and n ≥ 3, what is the previous odd number?
If n is odd and n ≥ 3, what is the previous odd number?
EXERCISE 5
Think of a ‘number’. Let this number be x.
Write the following using algebra to see what you get.
- Multiply the number you thought of by 2 and subtract 5.
- Multiply the result by 3.
- Add 15.
- Subtract 5 times the number you first thought of.
EXERCISE 6
Show that the sum of the first n odd numbers is n2.
Quotients of expressions involving pronumerals often occur. We call them algebraic fractions we will meet this again in the modules, Special Expansions and Algebraic Fractions.
EXAMPLE
Write each of the following in algebraic notation.
a![]() A number is divided by 5, and 6 is added to the result.
A number is divided by 5, and 6 is added to the result.
b![]() Five is added to a number, and the result is divided by 3.
Five is added to a number, and the result is divided by 3.
Solution
a |
Let x be the number. |
Dividing by 5 gives |
|
Adding 6 to this result gives 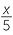 + 6. + 6. |
|
| b | Let the number be x. |
| Adding 5 gives x + 5. | |
Dividing this by 3 gives 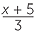 . . |
Notice that the vinculum acts as a bracket.
EXAMPLE
If x = 10, find the value:
a![]()

![]() b
b![]()
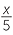 + 3
+ 3 ![]() c
c![]()
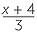
![]() d
d![]()
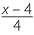
Solution
| a |  |
= 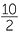 |
b | 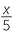 + 3 + 3 |
= 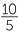 + 3 + 3 |
|||||
| = 5 | = 5 | |||||||||
| c | 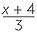 |
= 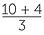 |
d | 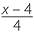 |
= 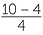 |
|||||
= 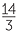 |
=  |
|||||||||
= 4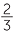 |
=  |
|||||||||
EXAMPLE
A vat contains n litres of oil. Forty litres of oil are then added to the vat.
a![]() How many litres of oil are there now in the vat?
How many litres of oil are there now in the vat?
b![]() The oil is divided into 50 containers. How much oil is there in each container?
The oil is divided into 50 containers. How much oil is there in each container?
Solution
a![]() There is a total of n + 40 litres of oil in the vat.
There is a total of n + 40 litres of oil in the vat.
b![]() There are
There are 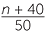 litres of oil in each container.
litres of oil in each container.
EXERCISE 7
A shed contains n tonnes of coal. An extra 1000 tonnes are then added.
- a
- How many tonnes of coal are there in the shed now?
- b
- It is decided to ship the coal in 10 equal loads. How many tonnes of coal are there in each load?
Expanding brackets and collecting like terms
Expanding brackets
Numbers obey the distributive laws for multiplication over addition and subtraction. For example:
![]() 3 × (4 + 5) = 3 × 4 + 3 × 5
3 × (4 + 5) = 3 × 4 + 3 × 5 ![]() 7 × (6 − 3) = 7 × 6 − 7 × 3
7 × (6 − 3) = 7 × 6 − 7 × 3
The distributive laws for division over addition and subtraction also hold as shown.
For example:
![]() (8 + 6) ÷ 2 = 8 ÷ 2 + 6 ÷ 2
(8 + 6) ÷ 2 = 8 ÷ 2 + 6 ÷ 2![]() and
and![]()
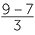 =
= 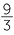 −
− 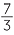
As with adding like terms and multiplying terms, the laws that apply to arithmetic can be extended to algebra. This process of rewriting an expression to remove brackets is usually referred to as expanding brackets.
EXAMPLE
Use the distributive law to rewrite these expressions without brackets.
a![]() 5(x − 4)
5(x − 4) ![]() b
b![]() 4(3x + 2)
4(3x + 2) ![]() c
c![]() 6(4 − 2x)
6(4 − 2x)
Solution
a![]() 5(x − 4) = 5x − 20
5(x − 4) = 5x − 20 ![]() b
b![]() 4(3x + 2) = 12x + 8
4(3x + 2) = 12x + 8
c![]() 6(4 − 2x) =24 − 12x
6(4 − 2x) =24 − 12x
EXAMPLE
Use the distributive law to rewrite these expressions without brackets.
|
a |
|
b |
|
Solution
|
a |
|
b |
|
Collecting like terms
After brackets have been expanded like terms can be collected.
EXAMPLE
Expand the brackets and collect like terms:
a![]() 2(x − 6) + 5x
2(x − 6) + 5x ![]() b
b![]() 3 + 3(x − 1)
3 + 3(x − 1) ![]() c
c![]() 3(2x + 4) + 6(x − 1)
3(2x + 4) + 6(x − 1)
Solution
a![]() 2(x − 6) + 5x = 2x − 12 + 5x = 7x − 12
2(x − 6) + 5x = 2x − 12 + 5x = 7x − 12 ![]() b
b![]() 3 + 3(x − 1) = 3 + 3x − 3 = 3x
3 + 3(x − 1) = 3 + 3x − 3 = 3x
c![]() 3(2x + 4) + 6(x − 1) = 6x + 12 + 6x − 6 = 12x + 6
3(2x + 4) + 6(x − 1) = 6x + 12 + 6x − 6 = 12x + 6
EXERCISE 8
Expand the brackets and collect like terms:
a![]() 5(x + 2) + 2(x − 3)
5(x + 2) + 2(x − 3) ![]() b
b![]() 2(7 + 5x) + 4(x + 6)
2(7 + 5x) + 4(x + 6)
c![]() 3(2x + 7) + 2(x − 5)
3(2x + 7) + 2(x − 5)
A sound understanding of algebra is essential for virtually all areas of mathematics.
The introduction to algebra is continued in the modules, Negatives and the Index Laws in Algebra, Special Expansions and Algebraic Fractions and Fractions and the Index Laws in Algebra.
It was only in the 17th century that algebraic notation similar to that used today was introduced. For example, the notation used by Descartes (La Geometrie, 1637) and Wallis (1693) was very close to modern notation. However, algebra has a very long history.
There are examples of the ancient Egyptians working with algebra. About 1650 BC, the Egyptian scribe Ahmes made a transcript of even more ancient mathematical scriptures dating to the reign of the Pharaoh Amenemhat III. In 1858 the Scottish antiquarian, Henry Rhind, came into possession of Ahmes's papyrus. The papyrus is a scroll 33 cm wide and about 5.25m long filled with mathematical problems. One of the problems is as follows:
100 measures of corn must be divided among 5 workers, so that the second worker gets as many measures more than the first worker, as the third gets more than the second, as the fourth gets more than the third, and as the fifth gets more than the fourth. The first two workers shall get seven times fewer measures of corn than the three others. How many measures of corn shall each worker get? (The answer involves fractional measures of corn. Answer: 1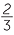 , 10
, 10 , 20, 29
, 20, 29 and 38
and 38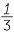 measures.)
measures.)
Euclid (circa 300 BC) dealt with algebra in a geometric way and algebraic problems are solved without using algebraic notation of any form. Diophantus (circa 275 AD ) who is sometimes called the father of algebra, produced a work largely devoted to the ideas of the subject.
Chinese and Indian authors wrote extensively on algebraic ideas and achieved a great deal in the solution of equations. The earliest Chinese text with algebraic ideas is The Nine Chapters on the Mathematical Art, written around 250 BC. A later text is Shu-shu chiu-chang, or Mathematical Treatise in Nine Sections, which was written by the wealthy governor and minister Ch'in Chiu-shao (circa 1202 − circa 1261 AD).
In approximately 800 BC an Indian mathematician Baudhayana, in his Baudhayana Sulba Sutra, discovered Pythagorean triples algebraically, and found geometric solutions of linear equations and quadratic equations of the forms, ax2 = c and of ax2 + bx = c.
In 680 AD the Indian mathematician Brahmagupta, in his treatise Brahma Sputa Siddhanta, worked with quadratic equations and determined rules for solving linear and quadratic equations. He discovered that quadratic equations can have two roots, including both negative and irrational roots.
Indian mathematician Aryabhata, in his treatise Aryabhatiya, obtains whole-number solutions to linear equations by a method equivalent to the modern one.
Arab and Persian mathematicians had an interest in algebra and their ideas flowed into Europe. One algebraist of special prominence was al-Khwarizmi, whose al-jabr w’al muqabalah (circa 825 AD) gave the discipline its name and gave the first systematic treatment of algebra.
The works of al-Khwarizmi were translated into European languages by several different translators during the twelfth century and so his and other Arab writers’ work were well known in Europe.
 Fibonacci was the greatest European writer on algebra during the middle ages and his work Liber Quadratorum (circa 1225 AD) includes many different ingenious ways of solving equations.
Fibonacci was the greatest European writer on algebra during the middle ages and his work Liber Quadratorum (circa 1225 AD) includes many different ingenious ways of solving equations.
Cardano, Tartaglia (16th century), Vieta (16th − 17th century) and others developed the ideas and notation of algebra. The Ars Magna (Latin: “The Great Art”) is an important book on Algebra written by Gerolamo Cardano. It was first published in 1545 under the title Artis Magnæ, Sive de Regulis Algebraicis Liber Unus (Book number one about The Great Art, or The Rules of Algebra). There was a second edition in Cardano’s lifetime, published in 1570. It is considered one of the three greatest scientific treatises of the Renaissance. The book included the solutions to the cubic and quartic equations. The solution to one particular case of the cubic, x3 + ax = b (in modern notation), was communicated to him by Niccolò Fontana Tartaglia, and the quartic was solved by Cardano’s student Lodovico Ferrari.
Development of algebraic notation
Here are some of the different notations used from the Middle Ages onwards together with their modern form. They reveal how useful modern algebraic notation is.
|
Trouame.1.n0.che gi |
|
|
|
4 Se. −51 Pri. −30 N. dit is ghelijc 45 |
|
|
|
cub p: 6 reb æ |
|
|
|
1 Q C −15 Q Q + 85 C −225 Q + 274 N æquator 120. |
|
|
|
aaa − 3.bba ======= + 2.ccc |
|
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
Exercise 1
a![]() n − 3 bananas in each crate
n − 3 bananas in each crate ![]() b
b![]() 7(n − 3) bananas in total
7(n − 3) bananas in total
Exercise 2
a![]() 20(s + 5) seats in total
20(s + 5) seats in total
Exercise 3
a![]() 270
270 ![]() b
b![]() 27 000
27 000
Exercise 4
a![]() b + 2
b + 2 ![]() b
b![]() a + 3, a + 6
a + 3, a + 6 ![]() c
c![]() n − 2
n − 2
Exercise 5
x  2x − 5
2x − 5  3(2x − 5) = 6x − 15
3(2x − 5) = 6x − 15  6x
6x  6x − 5x = x
6x − 5x = x
Exercise 6
Sum of the first n odd numbers is: 1 + 3 + 5 + …. + (2n − 5) + (2n − 3) + (2n − 1)
Reverse the sum: (2n − 1) + (2n − 3) + (2n − 5) + … + 5 + 3 + 1
Add to the original sum pairing terms yields
(2n − 1 + 1) + (2n − 3 + 3) + … + (3 + 2n − 3) + (1 + 2n − 1) = 2n × n =2n2
The sum is n2
Exercise 7
a![]() n + 1000 tonnes
n + 1000 tonnes ![]() b
b![]()
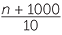 tonnes
tonnes
Exercise 8
a![]() 7x + 4
7x + 4 ![]() b
b![]() 14x + 38
14x + 38 ![]() c
c![]() 8x + 11
8x + 11
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()