The Improving Mathematics Education in Schools (TIMES) Project
- Familiarity with simple word problems.
- Facility with basic algebra, including the use of the distributive law to expand brackets.
- Familiarity with fractions and integers.
- Familiarity with simple algebraic fractions.
In Primary School a common method of reinforcing arithmetic skills is to ask students questions such as:
Which number when added to 5 gives 13?
Which number when multiplied by 7 gives 56?
Which number when subtracted from 23 gives 14?
An equation is a way of expressing such problems in a symbolic format, so that more complicated questions can be asked and solved.
The three questions above can be written as the equations:
x + 5 = 13,![]() 7x = 56,
7x = 56,![]() 23 − x = 14
23 − x = 14
where in each case x is the unknown number to be found.
Finding the value of the unknown is called solving the equation. Such a value of is called the solution of the equation, and is said to satisfy the equation.
The more complicated equation 3x − 4 = 11 could be expressed as:
![]() Three times what number gives 11 when 4 is subtracted?
Three times what number gives 11 when 4 is subtracted?
Equations such as these can be solved intuitively using only our knowledge of basic arithmetic, especially since the answers are all whole numbers. We would like to be able to solve more complicated equations whose solutions are rational or real numbers, and so we need to develop some standard strategies for doing this. For example: What is the radius of a circle whose perimeter is 5cm?
Equations arise very naturally when solving problems. In fact, a lot of problem-solving relies on us being able to translate a given word or real-world problem into an equation, or equations, solve the equation(s) and relate the solution to the original problem. Turning a complicated problem into an equation enables us to understand and solve difficult problems. Before we reach this stage, we need to have at hand a collection of techniques for solving equations.
In earlier times, people used a number of ad hoc methods for solving equations. It was only since the development of modern algebra that standard procedures and notations have been constructed that enable us to solve equations quickly and efficiently.
It is important when setting out the solution to an equation that each step is written under the previous one with the equal signs aligned. This careful setting out allows the logic of the solution to flow properly, and makes the algebra easy to check. Unsystematic methods, such as guess and check will generally be of limited use for more complicated equations.
The equations that we deal with in this module are called linear equations since they are related to the equation of a straight line.
Equations, expressions and identities
Students need to clearly understand the difference between an equation, an expression and an identity. These are all different, but can easily become confused in a student’s mind.
An expression is simply a quantity expressed symbolically, such as 5x + 6. Here, the pronumeral x (see module Algebraic Expressions)stands for any number, unless restricted by the context. We can, if required, substitute any value of x into the expression to produce a number.
An equation is a statement involving the equality of two expressions, in which the equality is true for some, but not necessarily all, values of the pronumeral. Thus, for example, the equation 3x − 4 = 11 is only true when takes the value 5. If we substitute any other value, the resulting statement is false. The equation x2 = 9 has solutions x = 3 or x = −3 since these are the only values of x that make the statement true.
An identity is a statement involving the equality of two expressions, in which the equality is true for all values of the pronumeral(s).
For example, the statement
![]() (x + 1)2 = x2 + 2x + 1
(x + 1)2 = x2 + 2x + 1
is true for all values of x, so the statement is an identity.
Similarly,
![]() a2 − b2 = (a − b)(a + b)
a2 − b2 = (a − b)(a + b)
is true for all values of a and b so it is an identity − generally known as the difference of squares.
We cannot `solve’ expressions, nor is there any point in solving identities.
Some equations have infinitely many solutions. For example, there are infinitely many values of x and y which make the statement x + y = 3 true.
If we restrict x and y to be whole numbers, then the only solutions to x + y = 3 are
![]() x = 0, y = 3;
x = 0, y = 3;![]() x = 1, y = 2;
x = 1, y = 2;![]() x = 2, y = 1;
x = 2, y = 1;![]() and x = 3, y = 0.
and x = 3, y = 0.
Some equations have no solutions. For example there is no real value of x such that x2 = −1
In this module we will only be concerned with equations in one unknown, not involving squares, higher powers, and so on; such equations are called linear equations.
Once we have solved an equation, we can always check that our solution is, in fact, correct. This is important, since in later work, the methods of solution may produce several answers, not all of which are valid solutions to the original problem. Such solutions are sometimes called extraneous solutions. They typically arise when we have squared both sides of an equation.
When solving linear equations, we perform operations to both sides of the equation in such a way that the solution of the modified equation is the same as the solution of the original equation.
One-step equations
The equation x + 3 = 7 may be interpreted as: What number when added to 3 gives 7? To find the value of we need to subtract 3 from 7. Thus, we may write the solution to the problem as:
| x + 3 | = 7 | ||
 |
x | = 7 − 3 | |
| x | = 4 |
To go from the first step to the second, we subtract 3 from both sides, noting that
x + 3 − 3 = 7 − 3, so subtracting 3 removes the +3 from the left-hand side of the equation. Since we subtract 3 from the left-hand side, we must also subtract 3 from the right-hand side. A standard model for explaining this is to think of a balance with the fulcrum at the equal sign. To maintain the balance, if we take 3 from one side, we need to take 3 from the other.
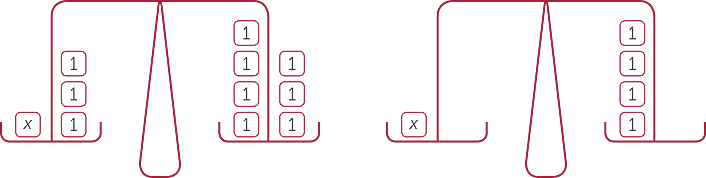
This illustrates the general principle that if we add a number to, or subtract a number from, the left-hand side, we do the same to the right-hand side. This maintains the equality of the two sides and ensures that any solution of the original equation is the also a solution of the modified equation. Similarly, we can multiply or divide both sides of an equation by the same non-zero number without changing the solutions to the equation.
It may be helpful to students to write the performed operation in a box over to the side.
We solve as follows:
| x − 3 | = 12 | ||
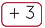 |
x − 3 | = 12 | |
| x | = 15 |
In the first step we add 3 to both sides to remove the −3 from the left hand side. Since we add 3 to the left hand side, we must add 3 to the right hand side.
A similar procedure applies to solving the equation 5x = 30.
| 5x | = 30 | ||
 |
x | = 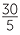 |
|
| x | = 6 |
Since x is multiplied by 5 in the given equation, we divide both sides by 5. In the same way, to solve  = 12, we will multiply both sides by 4, thus:
= 12, we will multiply both sides by 4, thus:
 |
= 12 | ||
 |
x | = 4 × 12 | |
| x | = 48. |
Adding or subtracting the same number to both sides of an equation produces an equivalent equation. Similarly, multiplying or dividing both sides of an equation by the same (non-zero) number produces an equivalent equation.
When we write a string of linear equations, we tacitly assume that each equation is equivalent to the previous one.
Equivalent equations have exactly the same solutions.
Equations involving more than one step
To solve an equation such as 2x + 3 = 15, we first produce an equivalent equation by subtracting 3 from both sides, we can then divide both sides by 2.
| 2x + 3 | = 15 | ||
 |
2x | = 12 | |
 |
x | = 6 |
We can quickly check the solution is correct, since 2 × 6 + 3 = 15.
Similarly, to solve we add 2 to both sides to produce an equivalent equation and then multiply both sides by 4.
 − 2 − 2 |
= 8 | ||
 |
 |
= 10 | |
 |
x | = 40 |
Consider the problem: I think of a number, double it and subtract 3. This gives me the number I started with plus 5. What is the number?
As usual, we let x denote the number. Then the equation corresponding to the given problem is
![]() 2x − 3 = x + 5.
2x − 3 = x + 5.
In this case, the unknown is on both sides of the equation. The first step is generally to collect all the unknowns together. If we subtract from both sides, we obtain x − 3 = 5, using the fact that 2x − x = x. We can then add 3 to both sides and solve the equation. Thus:
| 2x − 3 | = x + 5 | ||||
| x − 3 | = 5 | Subtract x from both sides | |||
 |
x | = 8. |
EXERCISE 1
Solve 5x − 14 = 2x − 2.
In the examples so far, the solutions have been positive integers. In general, the solutions may be integers or rational numbers.
EXAMPLE
Solve
a![]() 5x + 17 = 2
5x + 17 = 2![]() b
b![]() 7x −
7x −  =
=  − x.
− x.
Solution
| a | 5x + 17 = 2 | b |
7x −  = = 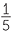 − x − x |
||||||||
 |
5x | = 2 − 17 |  , , |
7x + x | = 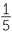 + +  |
||||||
| 5x | = −15 | 8x | = 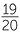 |
||||||||
 |
x | = −3. |  |
x | = 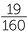 . . |
From here on, we will generally not bother to indicate every operation in a box.
If we encounter an equation containing brackets, it may be necessary to expand the brackets and simplify before continuing to isolate the unknown using the methods shown above.
EXAMPLE
Solve
a![]() 2(3z + 4) + 5 = 21
2(3z + 4) + 5 = 21 ![]() b
b![]() 5(a − 2) + 9 = 3(2a − 1)
5(a − 2) + 9 = 3(2a − 1)
Solution
| a | 2(3z + 4) + 5 | = 21 | b | 5(a − 2) + 9 | = 3(2a − 1) | |||
| 6z + 8 + 5 | = 21 | 5a − 10 + 9 | = 6a − 3 | |||||
| 6z + 13 | = 21 | −1 + 5a | = 6a − 3 | |||||
| 6z | = 8 | 2 | = 6a − 5a | |||||
| z | = 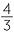 |
a | = 2 |
Note that as in the second example, it is better to move the unknowns to whichever side has the highest coefficient of the unknown. This will avoid the need to divide by a negative number.
It is easy to check mentally that the solution is correct by substituting into the original equation.This can also be performed more formally. For example, to check the second example above, we can write:
| When a = 2, LHS | = 5(a − 2) + 9 |
| = 5(2 − 2) + 9 | |
| = 9 | |
| RHS | = 3(2 × 2 − 1) = 9 = LHS. |
EXERCISE 2
Solve 4(2x − 3) = 8 − 6(4 − 5x).
Some equations involve fractions. The basic goal of isolating the unknown remains the same, but we need to get rid of the denominators. There are two main methods for solving these sorts of equations.
For example, to solve 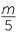 +
+  = 8, we could begin by placing the terms on the left hand side over a common denominator, 15.
= 8, we could begin by placing the terms on the left hand side over a common denominator, 15.
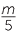 + +  |
= 8 | ||
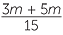 |
= 8 | ||
 |
8m | = 8 × 15 | |
 |
m | = 15 |
An alternative method is to multiply both sides of the equation by the (lowest) common denominator of the two fractions, which in this case is 15. This removes all the fractions in one step.
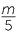 + +  |
= 8 | |||
 |
3m + 5m | = 8 × 15 | ||
| 8m | = 8 × 15 | |||
| m | = 15 |
EXAMPLE
Solve 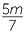 +
+ 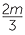 = 6.
= 6.
Solution
We use the second method and multiply both sides by 21.
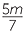 + + 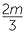 |
= 6 | |||
 |
15m + 14m | = 126 | ||
| 29m | = 126 | |||
| m | = 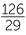 |
|||
= 4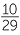 . . |
EXERCISE 3
Solve 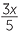 − 20 =
− 20 =  .
.
Impossible Equations and Identities
In all the examples dealt with above, applying the rules produced an equation with the unknown on one side and a single number on the other. That is the equation had just one solution.
Equations with no solutions
If we apply these rules to the equation
![]() 3x = 2(x + 1) + x
3x = 2(x + 1) + x
| we obtain | 3x | = 2(x + 1) + x | |
| 0 | = 2 |
This is clearly impossible. Hence the original equation has no solution.
That is, there is no value of x for which 3x = 2(x + 1) + x.
Identities
Similarly, applying the rules to
![]() 2(2x − 1) = (x + 1) + 3(x − 1)
2(2x − 1) = (x + 1) + 3(x − 1)
produces
| 4x − 2 | = x + 1 + 3x − 3 | |
| 4x − x − 3x | = 1 − 3 + 2 | |
| 0 | = 0 |
Since this last statement is always true, the equation we started with is true for all values of x and so is, in fact, an identity.
problems leading to linear equations
Equations are very useful in solving problems. The basic technique is to determine what quantity it is that we are trying to find and make that the unknown. We then translate the problem into an equation and solve it. You should always try to minimise the number of unknowns. For example, if we are told that a piece of rope 8 metres long is cut in two and one piece is x metres, then we can write the remaining piece as (8 − x) metres, rather than introducing a second unknown.
EXAMPLE
Josephine bought a desktop computer and printer at a total cost of $2203.50. The desktop cost 5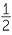 times as much as the printer. What was the cost of each item?
times as much as the printer. What was the cost of each item?
Solution
Although there are two costs we are looking for, we always try to minimise the number of unknowns. Hence,
Let x be the cost of the printer.
The cost of the computer is $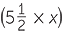 = $
= $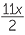 .
.
The total cost is $2203.50.
| Hence | 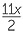 + x + x |
= 2203.50 | |||
 |
11x+ 2x | = 4407 | |||
| 13x | = 4407 | ||||
| x | = 339. |
The printer cost $339 and the computer cost $2203.50 − $339 = $1864.50.
EXAMPLE
Grant runs half the distance to school and walks for the remainder of the journey. He runs at 3 m/s but slows to 2 m/s for the second half of this trip. He takes 50 minutes to complete the trip. Find the distance Grant has to travel to school.
Solution
We will use metres and seconds as our units. Let x metres be half the distance to the school. Recall that distance = speed × time.
![]() and therefore
and therefore
![]() time =
time =  .
.
Then![]() time spent running at 3 m/s =
time spent running at 3 m/s = 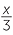
and![]() time spent moving at 2 m/s =
time spent moving at 2 m/s = 
Also,![]() time taken for the entire trip = 50 minutes = 3000 seconds.
time taken for the entire trip = 50 minutes = 3000 seconds.
| So | 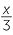 + +  |
= 3000 | |||
 |
2x + 3x | = 18000 | (Find a common denominator.) | ||
| 5x | = 18 000 | (Multiple both sides of the equation by 6.) | |||
 |
x | = 3600 |
Half the distance is 3600 metres. So the full distance is 7200 metre.
EXERCISE 4
David travels from town A to town B. He walks half the distance at 3km/h and runs the other half at 9km/h. The total time for the journey is 4 hours. What it the distance from A to B?
A simple extension of the types of equations dealt with above, is to combine brackets
and fractions.
EXAMPLE
Solve 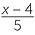 +
+  = 3.
= 3.
Solution
We multiply by the lowest common denominator, 30.
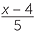 + + 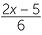 |
= 3 | |||
 |
6(x − 4) + 5(2x − 5) | = 90 | ||
| 6x − 24 + 10x − 25 | = 90 | |||
| 16x − 49 | = 90 | |||
| 16x | = 139 | |||
| x | = 8 . . |
EXERCISE 5
Solve 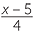 +
+ 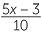 = −5.
= −5.
In some problems, one or more of the pieces of information might not be given explicitly as a number, but as a general quantity. Thus we may have an equation in which we have not only the unknown we seek, but also other pronumerals whose values we regard as given. In solving such an equation, we need to specify carefully which variable we are solving for. Equations such as this are sometimes referred to as literal equations.
EXAMPLE
Solve the equation for 5(x − a) + 2a = 3x + 7a − 2 for x.
Solution
We proceed using the usual rules, keeping our focus on the unknown x
| 5(x − a) + 2a | = 3x + 7a − 2 | |
| 5x − 5a + 2a | = 3x + 7a − 2 | |
| 5x − 3x | = 7a + 5a − 2a − 2 | |
| 2x | = 10a − 2 | |
| x | = 5a − 1. |
Note:The answer can be checked in the usual way
![]() LHS = 5(5a − 1 - a ) + 2a − 5 = 22a − 5
LHS = 5(5a − 1 - a ) + 2a − 5 = 22a − 5
![]() RHS = 3(5a − 1) + 7a − 2 = 22a − 5
RHS = 3(5a − 1) + 7a − 2 = 22a − 5
Therefore, LHS = RHS
Many problems involve finding values of two or more unknowns. These are often linked via a number of linear equations. For example, if I tell you that the sum of two numbers is
89 and their difference is 33, we can let the larger number be x and the smaller one y
and write the given information as a pair of equations:
![]() x + y = 89 (1)
x + y = 89 (1)
![]() x − y = 33. (2)
x − y = 33. (2)
These are called simultaneous equations since we seek values of x and y that makes both equations true simultaneously. In this case, if we add the equations we obtain 2x = 122,
so x = 61. We can then substitute this value back into either equation, say the first, then
61 + y = 89 giving y = 28.
More difficult examples of simultaneous equations and methods to solve them are studied in Years 9 and 10 and will be covered the module, Introduction to Coordinate Geometry.
All the equations treated up to now in this module are known as linear equations since the unknown x only appears to the first power. Each such equation was reducible to the form ax + b = c, from which we can solve for x.
Equations in which the unknown appears also to the power two are called
quadratic equations.
Quadratic equations have the general form ax2 + bx + c = 0, where a, b, c are given numbers. Such equations may have
- two distinct solutions
- one solution
- no solutions.
The techniques for solving these are covered in Years 9 and 10, and will be covered
the module, Quadratic Equations.
These types of equations are of tremendous importance in mathematics and its
many applications.
The Greek mathematician Diophantus wrote a collections of books in which he posed problems whose solutions were restricted to being whole numbers or rational numbers. Equations whose solutions are required to be integers are often referred to as
Diophantine equations.
We mentioned above the equation x + y = 3 . If we restrict x and y to be whole numbers, then the only solutions are:
![]() x = 0, y = 3;
x = 0, y = 3;![]() x = 1, y = 2;
x = 1, y = 2;![]() x = 2, y = 1;
x = 2, y = 1; ![]() and x = 3, y = 0.
and x = 3, y = 0.
A harder example, it to find all positive integer solutions to  +
+  =
=  .
.
The solution is very interesting.
Multiply the equation through by 6ab to remove all the fractions.
 + +  |
=  |
|
| 6b + 6a | = ab. |
We now take all the terms onto one side, add 36 to both sides and factorise.
| ab − 6a − 6b + 36 | = 36 | |
| (a − 6)(b − 6) | = 36. |
Now since the solutions are positive whole numbers, we equate each bracket with
a factor of 36. We will ignore the solution a = b = 0 since it does not satisfy the
original equation.
| a − 6 | b − 6 | a | b |
| 36 | 1 | 42 | 7 |
| 18 | 2 | 24 | 8 |
| 12 | 3 | 18 | 9 |
| 9 | 4 | 15 | 10 |
| 6 | 6 | 12 | 12 |
| 4 | 9 | 10 | 15 |
| 3 | 12 | 9 | 18 |
| 2 | 18 | 8 | 24 |
| 1 | 36 | 7 | 42 |
There is no systematic method for solving all diophantine equations. A toolkit of methods and techniques is helpful.
Solving of equations dates back to very early times. The Babylonians solved equations of the form ax = b by using lookup tables. They appear to have solved other simple linear equations by inspection.
The oldest known equation recorded by the Egyptians is in the Ahmes Papyrus. This was written about 1700 BC, but contains material that may go back much further. The problem is expressed as:
![]() Heap, its whole, its seventh, 19.
Heap, its whole, its seventh, 19.
The Egyptians used a symbol representing the Egyptian word for Heap as their unknown. Hence the equation above can be written as
![]() x +
x +  = 19.
= 19.
They developed a remarkable method for solving such equations in which all the unknowns are on one side and the constants on the other. This method will be outlined below. Its use continued through the centuries and during the Middle Ages, it came to be known as the Rule of False, or, in Latin, regula falsi. It was one of the standard methods for solving equations. A generalised double rule of false, was later developed to handle more general linear equations.
To make the arithmetic easier we demonstrate the rule by solving x +  = 24.
= 24.
- Step 1
- Make a guess. To avoid fractions we ‘guess’ x = 7.
- Step 2
- Substitute the guess into the left hand side. This gives 8.
- Step 3
- Take the right hand side, divide by the answer from Step 2 and multiply by the guess, thus x = 24 ÷ 8 × 7 = 21.
This is the correct answer!
In his book on mathematics Ground of Artes written in 1542, Robert Recorde wrote the following poem to accompany this method. (Recorde unfortunately ended his days in prison. Incidentally, Recorde gave us the equal sign, saying ‘No two things can be more equal than two parallel lines’.)
Geese at this woorke as happe doth leade.
By chaunce to truthe you may procede.
And firste woorke by the question.
Although no truthe therein be don.
Suche falsehode is so good a grounde,
That truth by it will soone be founde.
While this method is fun to do, it is not recommended that it be taught in the classroom. It only works when all the unknowns are on one side and the constants on the other and thus is of limited application.
EXERCISE 6
Use the rule of false to solve  +
+  = 27.
= 27.
- 1
- x = 4
- 2
- x =
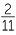
- 3
- x =
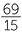 = 63
= 63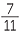
- 4
- 18 km
- 5
- x = −
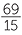 = −4
= −4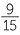
- 6
- Guess x = 20
LHS = 18 when x = 20
Take the quotient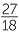 and multiply by the guess.
and multiply by the guess.
x =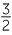 × 20 = 30
× 20 = 30
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

