The Improving Mathematics Education in Schools (TIMES) Project
Special Expansions and Algebraic Fractions
Number and Algebra : Module 25![]() Years : 8-9
Years : 8-9
June 2011
- The arithmetic of the rational numbers.
- Basic methods of mental arithmetic
- HCF and LCM in arithmetic
- Algebraic expressions and equations with rational numbers
- The index laws in algebra with whole−number indices
- Linear equations
The various uses of algebra require systematic skills in manipulating algebraic expressions. This module is the last of four modules that provide a systematic introduction to basic algebraic skills.
The second module dealt with the expansion of a pair of brackets using the distributive law. This module now introduces the expansion of two sets of brackets within the one expression, as in
![]() (x + 3)(x + 5) = x2 + 8x + 15.
(x + 3)(x + 5) = x2 + 8x + 15.
This leads to the three standard special expansions, and the use of these identities as formulae to expand at sight binomial squares and difference of squares expansions.
In the second half of the module, the idea of a fraction needs to be extended so that
we can deal with more general algebraic fractions such as
![]()

![]() and
and ![]()

![]() and
and ![]()
 .
.
Simple algebraic fractions were introduced in the third module of the series, but they are dealt with here in more detail − they need to be treated last because of the calculation difficulties that they can cause.
The next stage of development in algebra is systematic factoring of algebraic expressions. Everything has now been prepared for this task.
Expanding two or more sets of brackets
So far, we have only used the distributive law to expand expressions with one set of brackets,
![]() (x + 3)u = xu + 3u.
(x + 3)u = xu + 3u.
Now suppose that we want to expand an expression such as (x + 3)(x + 5) with two sets of brackets. The method is to expand one set, and then expand the other. In the first step below, we regard the (x + 5) as a single object, like u in the example above
| |
(x + 3)(x + 5) | = x(x + 5) + 3(x + 5) | |
Think of (x + 5) as a single object u. |
| = x2 + 5x + 3x + 15 | Now expand the brackets in (x + 5). | |||
| = x2 + 8x + 15 | Collect the terms at the end. |
This expansion has a useful representation using a dissection of a rectangle:
![]()

When there are negatives, the usual laws of signs apply,
| |
(x − 2)(6 − x) | = x(6 − x) − 2(6 − x) | |
Think of (6 − x) as a single object u. |
| = 6x − x2 − 12 + 2x | Now expand the brackets in (6 − x). | |||
| = −x2 + 8x − 12 | Collect the terms at the end. |
Alternatively, we could have expanded the second set of brackets first,
| |
(x − 2)(6 − x) | = (x − 2)6 − (x − 2)x | |
Think of (x − 2) as a single object u. |
| = 6x − 12 − x2 + 2x | Now expand the brackets in (x − 2). | |||
| = −x2 + 8x − 12 | Collect the terms at the end. |
The index laws may also be helpful, as in parts (c) and (d) below.
EXAMPLE
Expand and simplify:
| a | (x − 5)(x + 6) | |
b | (4 − 3x)(4 + 3x) | ||
| c | (x2 + x + 1)(x − 1) | d | (2x2 − 1)(x2 − 2) |
Solution
| a | (x − 5)(x + 6) | = x(x + 6) − 5(x + 6) | |
| = x2 + 6x − 5x − 30 | |||
| = x2 + x − 30 |
| b | (4 − 3x)(4 + 3x) | = 4(4 + 3x) − 3x(4 + 3x) | |
| = 16 + 12x − 12x − 9x2 | |||
| = 16 − 9x2 |
| c | (x2 + x + 1)(x − 1) | = x2(x − 1) + x(x − 1) + (x − 1) | |
| = x3 − x2 + x2 − x + x − 1 | |||
| = x3 − 1 |
| d | (2x2 − 1)(x2 − 2) | = 2x2(x2 − 2) − (x2 − 2) | |
| = 2x4 − 4x2 − x2 + 2 | |||
| = 2x4 − 5x2 + 2 |
Exercise 1
Expand and simplify (x − 3)(x − 5), and hence expand and simplify (x − 3)(x − 5)(x − 7).
Can you expand two pairs of brackets without working?
Before they study quadratics in detail, students will need to write down expansions such as
![]() (x − 5)(x − 7) = x2 − 12x + 35
(x − 5)(x − 7) = x2 − 12x + 35
without any working. Depending on their progress, this may or may not be the appropriate place to learn the skill.
The pattern is straightforward, and can be recognised from the example above:
- The coefficient of x is the sum of the two numbers. Here (−5) + (−7) = −12.
- The constant term is the product of the two numbers. Here (−5) × (−7) = 35.
Exercise 2
Expand the brackets in these expressions these— without working if you can.
a![]() (x + 4)(x + 9)
(x + 4)(x + 9) ![]() b
b![]() (x − 3)(x − 7)
(x − 3)(x − 7) ![]() c
c![]() (x − 12)(x + 5)
(x − 12)(x + 5) ![]() d
d![]() (x + 8)(x − 3)
(x + 8)(x − 3)
Exercise 3
- a
- Justify the rule above by expanding (x + a)(x + b), showing all steps.
- b
- In the case where x, a and b are all positive, illustrate by a dissection of a rectangle.
Three expansions are particularly important throughout algebra. Because they occur so often, and because they are later needed in reverse, they cannot be expanded every time. Instead, they need to be remembered and applied as formulas.
Students are usually quite insecure with these formulas at first, and may need to continue expanding brackets, as in the previous section, for some time before they trust the formulas.
The difference of squares
The first expansion is quite dramatic, because two terms cancel out with each other, leaving just two squares,
| (A − B)(A + B) | = A(A + B) − B(A + B) | |
| = A2 + BA − BA + B2 | ||
| = A2 − B2 |
This identity is called the difference of squares because the result is the difference of the squares A2 and B2. It is the most important algebraic identity in all school mathematics.
When we substitute values for A and B, we obtain arithmetic interpretations of the identity. For example, the reader can quickly check these identities by evaluating LHS and RHS separately,
![]() (5 − 2)(5 + 2) = 52 − 22
(5 − 2)(5 + 2) = 52 − 22 ![]() and
and![]() (7 − 3)(7 + 3) = 72 − 32.
(7 − 3)(7 + 3) = 72 − 32.
The identity also has a geometric interpretation as the difference between the area of two squares, and in this form it was well known to ancient Greek mathematicians. For example, if we read the identity (5 − 2)(5 + 2) = 52 − 22 backwards, it means that a square of side 5, with a square of side 2 cut out of it, can be cut up and rearranged into
a rectangle with sides 3 and 7 . This is easily done:
|
|
|
Applying the difference of squares identity in algebra
We have written the difference of squares identity in the form
![]() (A − B)(A + B) = A2 − B2.
(A − B)(A + B) = A2 − B2.
with the unusual symbols capital A and B used as pronumerals. The reason for this is that we can easily substitute more common algebraic symbols such as x and a. For example, using this formula, we can write down, without any middle steps,
![]() (x − 5)(x + 5) = x2 − 25
(x − 5)(x + 5) = x2 − 25 ![]() and
and![]() (3 − 2a)(3 + 2a) = 9 − 4a2.
(3 − 2a)(3 + 2a) = 9 − 4a2.
EXAMPLE
Use the difference of squares identity to expand:
| a | (x − 9)(x + 9) | b | (10 − x)(10 + x) | |||
| c | (3x + 1)(3x − 1) | d | (7x5 − 4a) (7x5 + 4a) | |||
Solution |
||||||
| a | (x − 9)(x + 9) = x2 − 81 | b | (10 − x)(10 + x) = 100 − x2 | |||
| c | (3x + 1)(3x − 1) = 9x2 − 1 | d | (7x5 − 4a) (7x5 + 4a) = 49x10 − 16a2 | |||
Using the difference of squares in mental arithmetic
Some products beyond the known tables can be calculated quickly using the difference of squares,
| 9 × 13 | = (11 − 2)(11 + 2) | 17 × 23 | = (20 − 3)(20 + 3) | ||
| = 112 − 22 | = 202 − 32 | ||||
| = 121 − 4 | = 400 − 9 | ||||
| = 117 | = 391 |
Such practice can help students to become familiar with such an important identity.
EXERCISE 4
Use the difference of squares identity to evaluate:
a![]() 7 × 17
7 × 17 ![]() b
b![]() 6 × 14
6 × 14 ![]() c
c![]() 28 × 32
28 × 32 ![]() d
d![]() 57 × 63
57 × 63
The identities for the square of a sum and the square of a difference
The other two special expansions are the square of a sum and the square of a difference.
| (A + B)2 | = (A + B)(A + B) | (A − B)2 | = (A − B)(A − B) | ||
| = A(A + B) + B(A + B) | = A(A − B) − B(A − B) | ||||
| = A2 + AB + AB + B2 | = A2 − AB − AB + B2 | ||||
| = A2 + 2AB + B2 | = A2 − 2AB + B2 |
Again, we can obtain arithmetic interpretations of this identity by substituting values of A and B. The reader can quickly check by substituting separately into LHS and RHS that
![]() (5 + 3)2 = 52 + 2 × 5 × 3 + 32
(5 + 3)2 = 52 + 2 × 5 × 3 + 32 ![]() and
and ![]() (5 − 3)2 = 52 − 2 × 5 × 3 + 32.
(5 − 3)2 = 52 − 2 × 5 × 3 + 32.
These identities were also known to the Greeks in their geometric form. The first identity above is a simple dissection of a square of side length 5 + 3 = 8. The second involves a slightly more elaborate dissection of a square of side length 5 = 3 + 2.
|
|
|
|
Exercise 5
Explain how the identity (5 − 3)2 = 52 − 2 × 5 × 3 + 32 can be related to areas on the right−hand diagram above.
Using the identities for the squares of a sum and difference in algebra
As with the difference of squares, we can apply these two formulas by substituting algebraic expressions for A and B into the two identities
![]() (A + B)2 = A2 + 2AB + B2
(A + B)2 = A2 + 2AB + B2 ![]() and
and![]() (A − B)2 = A2 − 2AB + B2.
(A − B)2 = A2 − 2AB + B2.
For example, without writing down any middle steps,
![]() (x + 7)2 = x2 + 14x + 49
(x + 7)2 = x2 + 14x + 49 ![]() and
and![]() (x − 7)2 = x2 − 14x + 49.
(x − 7)2 = x2 − 14x + 49.
Students commonly make errors with the middle term. The most secure approach to finding 2AB mentally is
- First find the product AB, then double it.
Notice that the minus sign is built into these formulas, so that you do not need to substitute negatives into them. This approach is uncommon in algebra, and is only done here because the two formulas are used so often that it is worth learning both forms.
The index laws may be needed, as in part d below.
EXAMPLE
Use the identities for the square of a sum and the square of a difference to expand:
| a | (x − 7)2 | b | (10 + x)2 | |||
| c | (6x − 1)2 | d | (5x4 + 8)2 | |||
Solution |
||||||
| a | (x − 7)2 = x2 − 14x + 49 | b | (10 + x)2 = 100 + 20x + x2 | |||
| c | 6x − 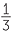 2 = 36x2 − 4x + 2 = 36x2 − 4x +  |
d | (5x4 + 8)2 = 25x8 + 80x4 + 64 | |||
Exercise 6
Expand (A + B)3, and hence expand (x + 5)3.
Using the identities for the squares of a sum and difference in mental arithmetic
These formulas are also quite useful in mental arithmetic, and once again, practising them with mental arithmetic is a very good way of learning them. For example,
| 212 | = (20 + 1)2 | 282 | = (30 − 2)2 | ||
| = 202 + 2 × 20 × 1 + 12 | = 302 − 2 × 30 × 2 + 22 | ||||
| = 400 + 40 + 1 | = 900 − 120 + 4 | ||||
| = 441 | = 784 | ||||
Exercise 7
Use the identities for the square of sum and the square of a difference to evaluate:
a ![]() 192
192 ![]() b
b ![]() 222
222 ![]() c
c ![]() 332
332 ![]() d
d ![]() 782
782
Substituting into algebraic fractions
An algebraic fraction is a fraction involving a pronumeral. Algebraic fractions were introduced in the previous module, Fractions and the Index Laws in Algebra, and this module extends that discussion to algebraic fractions such as
![]()
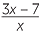
![]() and
and![]()
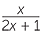
![]() and
and![]()
 .
.
whose numerators and denominators may be a sum or difference of terms. We need to be careful with such fractions not to make a substitution that would involve dividing by zero. For example:
 |
is undefined when x = 0 (and is never zero) | ||
 |
is undefined when x = 2 (and is zero when x = 0) | ||
 |
is undefined when x = −7 (and is zero when x = 3) |
- A fraction is undefined when its denominator is zero.
- A fraction is zero when its numerator is zero and its denominator is non−zero.
The last remark is intended to cover substitutions that make both numerator and denominator zero. Since the calculation ‘zero divided by zero’ is impossible, such substitutions are also not allowed:
 |
is undefined when x = 0 (and is equal to  for all other values of x). for all other values of x). |
||
 |
is undefined when x = 3 (and is equal to 2 for all other values of x). |
All other substitutions into algebraic fractions are simply applications of the arithmetic of positive and negative fractions.
EXAMPLE
First state when each algebraic fraction is undefined or zero, then substitute x = −1 into it.
into it.
a![]()

![]() b
b ![]()
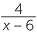
![]() c
c![]()

![]() d
d![]()

Solution
- a
-
 is undefined when x = 0, and is never zero.
is undefined when x = 0, and is never zero.
When x = −1 , , |
 |
=  |
||
=  |
(Double top and bottom) | |||
= −3 |
||||
| or |  |
=  × − × −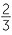 = −3 = −3 |
- b
-
 is undefined when x = 6, and is never zero.
is undefined when x = 6, and is never zero.
When x = −1 , , |
 |
=  |
|||
=  |
(Double top and bottom.) | ||||
= − |
|||||
- c
-
 is undefined when x = −2, and zero when x = −1.
is undefined when x = −2, and zero when x = −1.
When x = −1 , , |
 |
=  |
|||
=  |
(Double top and bottom.) | ||||
| = −1 |
- d
-
 is undefined when x = 2, and is equal to 5 for all other values of x, because the numerator is 5 times the denominator.
is undefined when x = 2, and is equal to 5 for all other values of x, because the numerator is 5 times the denominator.
Cancelling, multiplying and dividing algebraic fractions
The last part of the previous example was a little unsystematic in its method. The systematic approach is to factor numerator and denominator, and then cancel any common factors:
![]()
 =
=  = 5, provided that x ≠ 2.
= 5, provided that x ≠ 2.
Strictly speaking, the value x = 2 has to be excluded, because substitution of x = 2 into the original algebraic fraction gives ‘zero divided by zero’, which is certainly not 2. Even though this qualification will be important later in calculus, it is usually not appropriate for students at this stage. For completeness, however, we have added such qualifications in the examples below.
The example above shows what is required for cancelling, multiplying and dividing algebraic fractions:
- First, factor the numerator and denominator.
- Then cancel any common factors.
- For some students it may be appropriate at this stage to exclude impossible values of x.
EXAMPLE
Simplify each expression:
a![]()
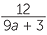
![]() b
b![]()
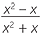
![]() c
c![]()

Solution
| a |  |
=  |
|
=  |
A routine mistake in this example is to cancel the 12 with the 9, but ignore the 3, giving the wrong answer  . The important instruction here is:
. The important instruction here is:
Factor first, then cancel.
| b |  |
=  |
|||
=  , , |
provided that x ≠ 0. | ||||
| c |  |
=  |
|||
=  , , |
provided that b ≠ 2 . . |
EXAMPLE
Simplify:
a![]()
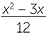 ×
× 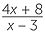
![]() b
b![]()
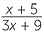 ÷
÷ 
Solution
| a |  × ×  |
= 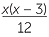 × ×  |
|||
=  , , |
|||||
| b | 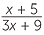 ÷ ÷  |
= 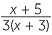 × ×  |
|||
=  , , |
|||||
Adding and subtracting algebraic fractions
Finding a common denominator is the key to adding and subtracting fractions, but we first need to look briefly at adding and subtracting fractions with a common denominator.
Adding and subtracting algebraic fractions that have a common denominator
When a fraction has two or more terms in its numerator, a negative sign in front of the fraction applies to the whole fraction.
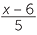 − −  |
=  |
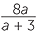 − −  |
=  |
||
=  |
=  |
||||
=  |
=  |
There are two important principles in the working above. First,
- Each vinculum acts as a bracket.
The setting out above is least likely to lead to error. In the first step, a single vinculum is used, and brackets are inserted instead. In the second step these brackets are expanded using the laws of signs.
- From now on, it is usually better to add and subtract fractions using a single vinculum.
EXAMPLE
Simplify each expression:
a![]()
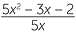 −
− 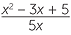
![]() b
b![]()
 −
− 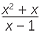 +
+ 
Solution
| a |  − −  |
=  |
|
=  |
|||
=  |
| b | 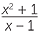 − − 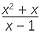 + +  |
=  |
|
=  |
|||
=  |
Adding and subtracting algebraic fractions that do not have a common denominator
When the fractions do not have a common denominator, the first step is to find one. Some factoring of the denominators may be necessary first.
EXAMPLE
Simplify each expression:
a![]()
 +
+ 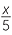
![]() b
b![]()
 +
+ 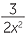
![]() c
c![]()
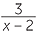 −
− 
Solution
- a
- With
 +
+  , the lowest common denominator is 5x.
, the lowest common denominator is 5x.
Multiply top and bottom of the first fraction by 5, and of the second by x.

 +
+ 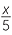 =
= 
- b
- With
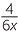 +
+  , the lowest common denominator is 6x2.
, the lowest common denominator is 6x2.
Multiply top and bottom of the first fraction by x, and of the second by 3.

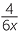 +
+ 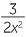 =
= 
- c
- First factor the second denominator.

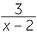 −
− 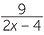 =
= 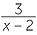 −
− 
Here the lowest common denominator is 2(x − 2).
Multiply top and bottom of the first fraction by 2, and leave the second fraction alone.
 =
= 
 =
= 
The example above should make it clear that there are three steps for finding the lowest common denominator when algebraic fractions are being added or subtracted:
- Factor the denominator.
- Find the LCM of the coefficients of the denominators.
- Choose the highest index of each algebraic factor that occurs.
The examples below are a little more elaborate, but illustrate the same steps.
EXAMPLE
Simplify:
a![]()
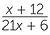 −
− 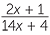
![]() b
b![]()
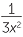 −
− 
Solution
a![]() First factor both denominators.
First factor both denominators.
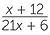 −
− 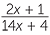 =
= 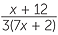 −
− 
The LCM of 2 and 3 is 6, so the lowest common denominator is 6(7x + 12).
Multiply top and bottom of the first fraction by 2, and of the second fraction by 3.
![]() =
= 
![]() =
= 
![]() =
= 
b![]() First factor the second denominator.
First factor the second denominator.
![]()
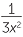 −
− 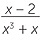 =
= 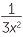 −
− 
The two powers of x are x1 and x2, so the lowest common denominator is 3x2(x2 + 1). Multiply top and bottom of the first fraction by (x2 + 1), and of the second fraction by 3x.
![]() =
= 
![]() =
= 
![]() =
= 
Equations involving algebraic fractions
As with all equations involving fractions, the next approach is usually:
- Multiply through by a common denominator of all the fractions so that the
fractions disappear.
EXAMPLE
Solve each equation:
a![]()
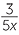 =
= 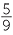
![]() b
b![]()
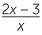 = 5
= 5 ![]() c
c![]()
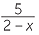 =
= 
Solution
a![]()
 =
= 
![]() Multiply both sides by 45x.
Multiply both sides by 45x.
| |
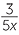 × ×  |
= 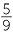 × ×  |
||
| 27 | = 25x |  |
||
| x | = 1 |
 |
b![]()
 = 5
= 5
Multiply both sides by x.
| |
2x − 3 | = 5x |  |
|
| −3 | = 3x |  |
||
| x | = −1 |  |
c![]()
 =
= 
Multiply both sides by x(2 − x).
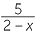 × ×  |
=  × ×  |
|||
| 5x | = 3x(2 − x) |  |
||
| 5x | = 6 − 3x | |||
| 8x | = 6 |  |
||
| x | =  |
 |
Exercise 8
Solve:
− +
+  −
−  +
+ 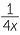 −
−  +
+  = −1.
= −1.
As mentioned in the Motivation section, this module is the fourth of four modules dealing with basic manipulation of algebraic expressions. The four modules are:
- Algebraic Expressions
- Negatives and the Index Laws in Algebra
- Fractions and the Index Laws in Algebra
- Special Expansions and Algebraic Fractions
The expansion of two sets of brackets is much harder to restore than the expansion of a single set of brackets. The careful two−step method of expansion given in this module is designed so that factoring is more easily seen as the reverse process of expansion. In particular, the steps involved in factoring by grouping and in the factoring of non−monic quadratics are simply the two−step expansion written out backwards:
| ax − ay + 4x − 4y | = a(x − y) + 4(x − y) | 6x2 + 13x + 6 | = 6x2 + 9x + 4x + 6 | |
| = (a + 4)(x − y) | = 3x(2x + 3) + 2(2x + 3) | |||
| = (3x + 2)(2x + 3) |
In the second factoring, the splitting of 13x into 9x + 4x was done in answer to the question, ‘Find two numbers whose sum is 13 and whose product is 6 × 6 = 36.’
The three special expansions of this module are more important in school mathematics because of their role in factoring than in expanding. Reversing the three special expansions relies on recognising that an expression is the RHS of one of the three identities. This is most important, and most obvious, with the differences of squares identity, whose name is based on the form of the RHS of the expansion. For example,
![]() x2 − 9 = (x − 3)(x + 3).
x2 − 9 = (x − 3)(x + 3).
Squares of sums and products should also be recognised when factoring,
![]() x2 + 6x + 9 = (x + 3)2 and x2 − 6x + 9 = (x − 3)2.
x2 + 6x + 9 = (x + 3)2 and x2 − 6x + 9 = (x − 3)2.
Completing the square is the most important of the various approaches to quadratics, because it applies to every quadratic, whether or not it can be factored using rational numbers. Completing the square involves first constructing the square of a sum or difference, then using the difference of squares identity,
| x2 + 6x + 5 | = (x2 + 6x + 9) + 5 − 9 | x2 + 6x + 2 | = (x2 + 6x + 9) + 2 − 9 | |
| = (x + 3)2 − 4 | = (x + 3)2 − 7 | |||
| = (x + 3 − 2)(x + 3 + 2) | = (x + 3 − 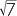 )( x + 3 + )( x + 3 +  ) ) |
|||
| = (x + 1)(x + 5) |
The three special expansions will each be generalised to any degree n in calculus, where they will become crucial in various contexts. The difference of squares becomes ‘the difference of nth powers’, and the expansion of the square of a binomial becomes what is known as ‘the binomial theorem’. Here are their analogues for degree 3:
| (A − B)(A2 + AB + B2) = A3 − B3 | (A + B)3 = A3 + 3A2B + 3AB2 + A3 | |
| (A + B)(A2 − AB + B2) = A3 + B3 | (A − B)3 = A3 − 3A2B + 3AB2 − A3 |
Algebraic fractions will be developed further once the factoring described above has been introduced. This will make further cancellation possible, and also lead to smaller common denominators when adding fractions. Algebraic fractions become routine in harder applications of calculus to, for example, motion problems, and they are required
in calculations associated with the rectangular hyperbola.
Exercise 1
| First, | (x − 3)(x − 5) | = x(x − 5) − 3(x − 5) | |
| = x2 − 5x − 3x + 15 | |||
| = x2 − 8x + 15. | |||
| Hence | (x − 3)(x − 5)(x − 7) | = (x2 − 8x + 15)(x − 7) | |
| = x2(x − 7) − 8x(x − 7) + 15(x − 7) | |||
| = x3 − 7x2 − 8x2 + 56x + 15x − 105 | |||
| = x3 − 15x2 + 71x − 105. |
Exercise 2
| a | (x + 4)(x + 9) = x2 + 13x + 36 | b | (x − 3)(x − 7) = x2 − 10x + 21 | |||
| c | (x − 12)(x + 5) = x2 − 7x − 60 | d | (x + 8)(x − 3) = x2 + 5x − 24 |
Exercise 3
| a | (x + a)(x + b) | = x(x + b) + a(x + b) | |
| = x2 + bx + ax + ab | |||
| = x2 + (a + b)x + ab. |
| b |  |
Exercise 4
| a | 7 × 17 | = 122 − 52 | b | 6 × 14 | = 102 − 42 | |||
| = 144 − 25 | = 100 − 16 | |||||||
| = 119 | = 84 | |||||||
| c | 28 × 32 | = 302 − 22 | d | 57 × 63 | = 602 − 32 | |||
| = 900 − 4 | = 3600 − 9 | |||||||
| = 896 | = 3591 |
Exercise 5
The rectangles TBCS and XYCD overlap in the square MYCS.
Hence Area ATMX = Area ABCD − Area TBCS − Area XYCD + Area MYCS.
Exercise 6
| (A + B)3 | = (A + B)2(A + B) |
| = (A2 + 2AB + B2)(A + B) | |
| = A2(A + B) + 2AB(A + B) + B2(A + B) | |
| = A3 + A2B + 2A2B + 2AB2 + AB2 + B3 | |
| = A3 + 3A2B + 3AB2 + B3 |
Substituting A = x and B = 5 into this formula gives (x + 5)3 = x3 + 15x2 + 75x + 125.
Exercise 7
| a | 192 | = 202 − 2 × 20 × 1 + 12 | b | 222 | = 202 + 2 × 20 × 2 + 22 | |||
| = 361 | = 484 | |||||||
| c | 332 | = 302 + 2 × 30 × 3 + 32 | d | 782 | = 802 − 2 × 80 × 2 + 22 | |||
| = 1089 | = 6084 |
Exercise 8
| Using the previous result, | Alternatively, multiply by 60x. | |||
− |
= −1 | −60 + 30 − 20 + 15 − 12 + 10 | = −60x | |
| x | =  |
−37 | = −60x  |
|
| x | =  |
|||
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()






