The Improving Mathematics Education in Schools (TIMES) Project
Students will have had extensive informal experience with geometry in earlier years of study.
In particular they should have met:
- The use of compasses, rulers, and set squares to draw geometrical figures involving straight lines and circles.
- Types of angles − right angles, acute angles, obtuse angles and reflex angles.
- Triangles, including an informal introduction to right-angled, isosceles and
equilateral triangles. - Quadrilaterals, including an informal introduction to parallelograms, trapezia, rhombuses, squares and rectangles.
- Informal experience with translations, reflections and rotations and with the idea
of symmetry.
A number of the ideas introduced in the module, Introduction to Plane Geometry, will be used in this module without redefinition. These ideas include points and lines, intervals, rays and angles, the size of an angle, vertically opposite angles, corresponding angles, alternate angles, co-interior angles, parallel lines, concurrent lines, collinear points and the angle sum of a triangle.
Architects, civil engineers, landscape architects and town planners among many other professionals have to be able to produce accurate plans well before the builder moves onto a site to begin construction. With the advent of CADCAM packages it is easy to forget that only thirty years ago technical drawing skills were an essential part of the education of all engineers and architects. In the same way as the electronic calculator does not remove the need to be able to calculate, CADCAM does not remove the need to be able to draw accurate figures.
The reasons for teaching geometric construction in junior high school are manifold. First, it reinforces the abstract ideas of length and angle size. In junior secondary school, degrees are universally used as the measure of angle size, leaving to Year 11 radians that are needed in the study of calculus. The unit of length most used in geometric constructions is the centimetre (cm) despite the fact that the official standards are the metre (m) and the millimetre (mm). This is because the centimetre is the most comfortable for diagrams drawn on A4 sheets of paper. We shall use centimetres throughout this module.
A free-hand sketch can be used if, for example, all that is needed to solve a problem is angle-chasing. However, in order to develop geometric understanding and to demonstrate (not prove) theorems, accurate drawings are required. For example, to demonstrate that two of the angles are equal in an isosceles triangle, an accurate sketch is needed.
In a more advanced topic, such as the study of congruence, accurate sketches are particularly useful. At the same time, the student can “discover” the triangle inequality
by trying to construct, for example, a triangle with sides 2, 3 and 8.
The Greeks certainly had the belief that all arithmetic should be grounded in geometry, and at one stage, thought that all numbers could be “constructed” with ruler and compasses. This is true for all rationals as well as for certain surds. We will discuss how to construct all the rationals (fractions) starting with a fixed unit length.

We will also show how to construct some regular polygons and briefly discuss why the three classical construction problems of the ancient Greeks are all impossible to carry out.
In the following, we follow a dual approach to justify the constructions. We shall generally use symmetry arguments and refer to congruence arguments.
Geometrical constructions should be drawn with a sharp, hard (2H) pencil. A pencil eraser, a ruler marked in centimetres (often used as a straight edge), a pair of compasses, two set squares (90°, 60°, 30° and 90°, 45°, 45°) and a protractor with a radius of at least 5cm make up the basic set of geometrical instruments. Students should be encouraged to draw accurate and large diagrams − a diagram which fits in a 3cm × 2cm box is rarely of any use at all.
Using compasses to draw a circle
Suppose we are given an interval AB and a point O. In geometry we always include the end points in an interval.

Open your compasses to the length of the interval AB. Then place the point of your compasses firmly into the point O. Holding the compasses only by the very top, draw a circle.
This is called drawing a circle with centre O and radius AB. Notice that every point on the circle is the same distance from the centre O, because the distance between the point O and the pencil lead never changes.
Here we will identify some important parts of a circle. We start by drawing a circle with centre O.
Radius
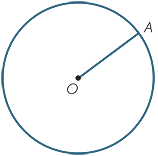 Draw an interval from any point A on the circle to the centre O.
Draw an interval from any point A on the circle to the centre O.
This interval AO is called a radius of the circle. Every radius of the circle has the same length, because the setting of the compasses remained the same while the circle was being drawn.
The word ‘radius’ is used both for the interval AO and for the length of the interval AO. ‘Radius’ is a Latin word meaning a spoke of a wheel. Its plural is ‘radii’.
Diameter
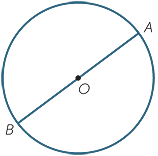 Draw a line through the centre O, cutting the circle at A and B.
Draw a line through the centre O, cutting the circle at A and B.
The interval AB is called a diameter of the circle. Every diameter has length twice that of any radius, because a diameter consists of two radii put together. The word ‘diameter’ is used both for the interval AB and for the length of the interval AB. It comes from Greek and means ‘to measure through’.
Chord
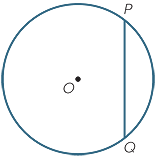 Choose any two distinct points P and Q on the circle,
Choose any two distinct points P and Q on the circle,
and join the interval PQ. This interval is called a chord
(from a Greek word meaning ‘a cord or string’).
Arc
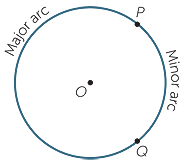 Choose two distinct points P and Q on the circle.
Choose two distinct points P and Q on the circle.
These two points divide the circle into two curved parts called arcs, each including the end-points P and Q. There are two arcs PQ. The larger arc is called the major arc PQ and the smaller arc is called the minor arc PQ. (“Major” and “minor” are the Latin words for “larger” and “smaller”; “arc” is from a Latin word for a bow or arch).
EXERCISE 1
Consider a fixed interval AB of length 8cm. Use constructions to show that there are exactly two triangles ABC and ABD with AC = AD = 5cm and BC = BD = 6cm.
Is triangle ABC a right-angled triangle?
Isosceles and equilateral triangles
 Triangles with two or three sides equal have some interesting
Triangles with two or three sides equal have some interesting
properties. Using simple constructions we can investigate
or demonstrate these properties.
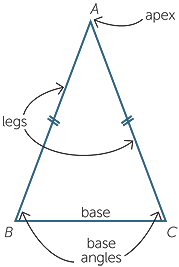
An isosceles triangle is a triangle with two (or more) sides equal.
- The equal sides AB and AC of the isosceles triangle ABC to the right are called the legs. They have been marked with double dashes to indicate that they are equal in length.
- The vertex A where the legs meet is called the apex and the third side BC is called the base.
- The angles
 B and
B and C at the base are called base angles.
C at the base are called base angles.
The word isosceles is a Greek word meaning “equal legs”. The prefix iso means “equal”, and −sceles is related to the word for leg.
Constructing an isosceles triangle and demonstrating the base angles are equal
Draw a large circle (or an arc) with centre A. Draw two radii AB and AC (A, B, C not collinear). Triangle ABC is isosceles. Check with a protractor that B =
B = C.
C.
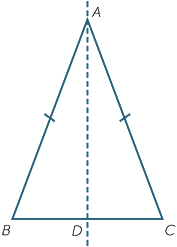 Note that the isosceles triangle ABC has an axis of symmetry AD with D the mid-point of BC.
Note that the isosceles triangle ABC has an axis of symmetry AD with D the mid-point of BC.
This means that reflecting  ACD in the line AD produces
ACD in the line AD produces  ABD. Alternatively, if we fold along the line AD, the points B and C coincide.
ABD. Alternatively, if we fold along the line AD, the points B and C coincide.
The converse is true
If a triangle has two equal angles, then the two sides opposite those angles are equal and the triangle is isosceles.
EXERCISE 2
Here is an investigation to illustrate the result.

Draw a long interval BC. Use a protractor to construct angles of 35° at B and C on the same side of the interval (any acute angle will do). Let the arms of these angles meet at A. Use compasses to confirm that the sides AB and AC opposite the equal angles have equal length. (There is a subtle difference between using compasses or dividers and measuring with the scale on a ruler.)
The formal proofs of the two results use simple congruence arguments and are covered in the module, Congruence.
Constructing an equilateral triangle using two circles
An equilateral triangle is a triangle in which all three sides have equal length.
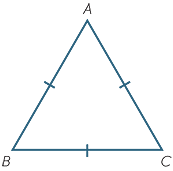 The diagram to the right shows an equilateral triangle ABC.Notice that it is an isosceles triangle in three different ways, because the base could be taken as AB, BC, or CA.
The diagram to the right shows an equilateral triangle ABC.Notice that it is an isosceles triangle in three different ways, because the base could be taken as AB, BC, or CA.
The word equilateral comes from Latin − equi means ‘equal’ and latus means ‘side’.
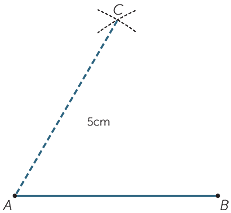 The construction is straightforward. Draw an interval AB of length, say, 5cm. Using compasses draw arcs of two circles centre A and B, both of radius 5cm. The point C is the point where the arcs meet.
The construction is straightforward. Draw an interval AB of length, say, 5cm. Using compasses draw arcs of two circles centre A and B, both of radius 5cm. The point C is the point where the arcs meet.
Since an equilateral triangle is isosceles with base AB,  A =
A = B. Similarly
B. Similarly  A =
A = C.
C.
But A +
A + B +
B + C = 180°, so all angles are 60°.
C = 180°, so all angles are 60°.
Basic constructions with straight edge and compass
Careful constructions with compasses and straight edge have always been an essential part of geometry. These constructions are based on a fundamental fact about circles:
All radii of a circle are equal.
Whenever you draw a circle using compasses, as the pencil lead moves, it always remains exactly the same distance from the fixed point.
Construction − Bisecting a given angle
The diagram below shows the steps to follow to bisect a given angle AOB.
AOB.
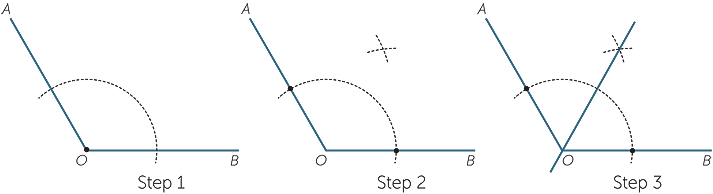
The two arcs in step 2 can have a different radius from the arc in step 1.
Folding the paper along the constructed line provides an informal proof or demonstration that the construction works. The arms OA and OB then fall exactly on top of each other, so AOB has been cut into two equal pieces. The formal proof uses SSS congruence.
AOB has been cut into two equal pieces. The formal proof uses SSS congruence.
The line you have constructed also bisects the reflex angle AOB. (Can you prove this?)
AOB. (Can you prove this?)
Construction − A right angle at the endpoint of an interval
A right angle is half a straight angle. Thus bisecting a straight angle using the previous construction will give a right angle. We begin by producing (extending) the interval BA.
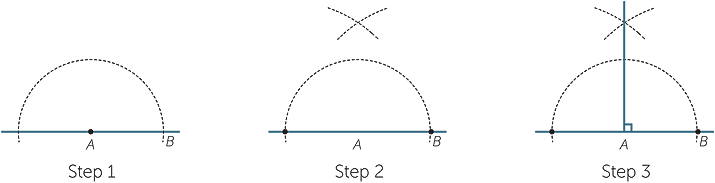
The two arcs in step 2 will need to have a larger radius than the arc in step 1.
Construction − An angle of 60° at the endpoint of an interval
The angles of an equilateral triangle are all 60°. Thus constructing an equilateral triangle will give an angle of 60°.
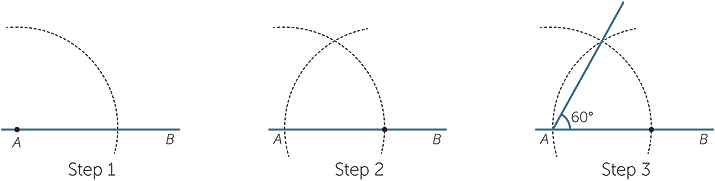
This time the arcs in steps 1 and 2 must have the same radius.
Construction − Further angles by bisection
Many other angles can now be constructed by applying the angle bisection construction to angles already constructed. For example:
- Bisecting 90° will give 45°.
- Bisecting again will give 22
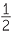 ° and 67
° and 67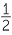 °.
°. - Bisecting 60° will give 30°.
- Bisecting again will give 15° and 75°.
Construction − The perpendicular bisector of an interval
Use these steps to bisect a given interval AB.
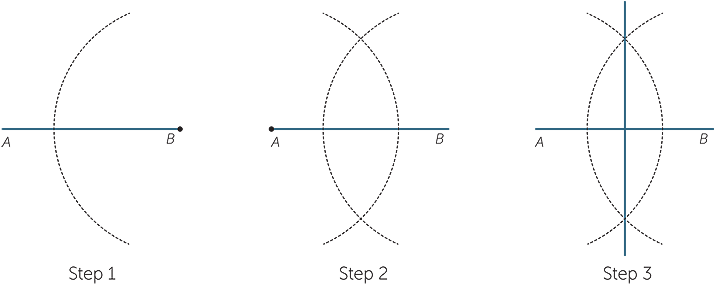
The arcs in steps 1 and 2 must have the same radius.
Informally speaking, the diagram is symmetric about the line you have constructed, as you can see by folding the paper along it. This means that the line bisects AB and is perpendicular to AB. The formal proof is essentially the proof that the diagonals of a rhombus bisect each other at right angles.
Note: You can use the above construction above to produce the midpoint of an interval, even if you do not actually need the perpendicular bisector.
Construction − Copying an angle
Use these steps to copy a given angle.
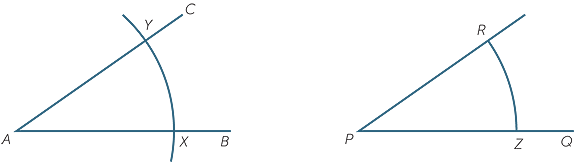
Let BAC be the given angle, and suppose that it is to be copied at vertex P and with one ray along PQ.
BAC be the given angle, and suppose that it is to be copied at vertex P and with one ray along PQ.
With centre A draw an arc cutting AB at X and AC at Y.
With centre P and the same radius AX, draw an arc cutting PQ at Z.
With centre Z and radius XY draw an arc cutting the previous arc at R.
Draw the ray PR. Then RPZ =
RPZ = A.
A.
Construction − Dropping a perpendicular from a point to a line
Use these steps to construct a line passing through a given point F and perpendicular to a given line AB.
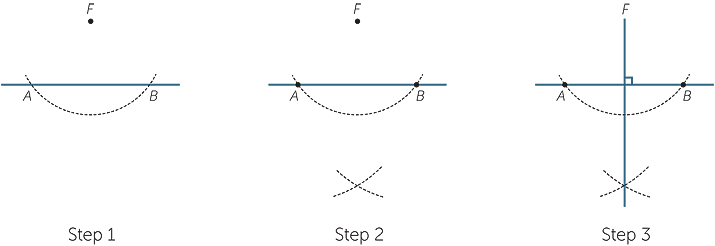
The two arcs in step 2 can have a different radius from the arc in step 1.
Informally speaking, the diagram is symmetric about the line you have constructed,
so the line is perpendicular to AB. (The quadrilateral is a kite!)
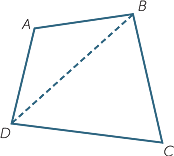
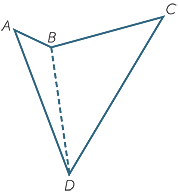
A quadrilateral is a plane figure with four sides.
 |
 |
|
| The quadrilateral on the left is called a convex quadrilateral because each of its four interior angles are less than 180o. |
The quadrilateral on the right is called a non-convex quadrilateral because one of its interior angles is a reflex angle. |
|
By dissecting a quadrilateral into two triangles, as shown above, and assuming that the sum of the angles in a triangle is 180°, we see that the sum of the angles in a quadrilateral is 360°.
There are a number of special quadrilaterals, which we shall discuss and construct below − parallelograms, rhombuses, trapezia, squares, rectangles, kites and cyclic quadrilaterals.
The parallelogram
There are a number of possible definitions for a parallelogram. We shall use the standard definition:
- A parallelogram is a quadrilateral whose opposite sides are parallel.
The basic properties of a parallelogram, which can be proved using easy congruence arguments, are:
- The opposite angles of a parallelogram are equal.
- The opposite sides of a parallelogram are equal.
Both of the above dot points have a natural converse.
- If a quadrilateral has opposite angles equal then it is a parallelogram.
- If a quadrilateral has opposite sides equal then it is a parallelogram.
These converses are true and give tests for a quadrilateral to be a parallelogram. See the module, Parallelograms and Rectangles.
The second dot point gives us the most straightforward method of construction
of a parallelogram:
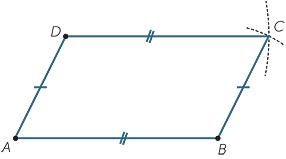
Choose three non-collinear points A, B and D. With radius AD make an arc centre B.
With radius AB mark an arc centre D. Let C be the point where the arcs meet. Then
ABCD is a parallelogram.
Note that there is a second figure, sometimes called a re-entrant quadrilateral that can be constructed using the same construction!
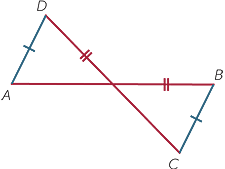
 A parallelogram can also be constructed by using the standard definition ‘A parallelogram is a quadrilateral whose opposite sides are parallel’. This is done by constructing two pairs of parallel lines by copying a given angle twice.
A parallelogram can also be constructed by using the standard definition ‘A parallelogram is a quadrilateral whose opposite sides are parallel’. This is done by constructing two pairs of parallel lines by copying a given angle twice.
 A line through a point parallel to a given line
A line through a point parallel to a given line
This is one of the most common constructions. There are various ways of performing this.
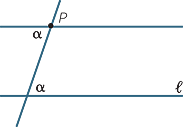 One can copy an angle:
One can copy an angle:
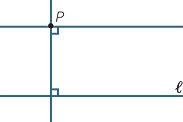 One can construct two perpendiculars:
One can construct two perpendiculars:
That is, drop a perpendicular from P to  and then construct a perpendicular at P.
and then construct a perpendicular at P.
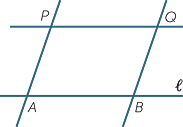 A third method is to choose two points A, B and construct the parallelogram ABQP using the construction in the previous section.
A third method is to choose two points A, B and construct the parallelogram ABQP using the construction in the previous section.
This is probably the simplest construction.
The rhombus
Once again various definitions are possible. The most natural and the traditional is:
- A rhombus is a quadrilateral in which all four sides are equal.
Some basic theorems about the rhombus are:
- The opposite sides of a rhombus are parallel.
- A parallelogram with a pair of adjacent sides equal is a rhombus.
- A quadrilateral in which the diagonals bisect each other at right angles is a rhombus.
See module, Rhombuses, Kites and Trapezia.
To construct a rhombus choose three non-collinear points A, B and D, with AB = AD. Construct C, as for the parallelogram, then ABCD is a rhombus.
The third dot point above gives an alternative construction.
The trapezium
A trapezium is a quadrilateral with one pair of opposite sides parallel.
 To construct a trapezium through P and
To construct a trapezium through P and  construct m through P parallel to
construct m through P parallel to  and then choose two points on
and then choose two points on  and two points on m.
and two points on m.
The rectangle
Once again a number of definitions are possible.
The most natural definition of a rectangle is:
- A rectangle is a quadrilateral in which all four angles are right angles.
Clearly, a rectangle is a parallelogram (co-interior angles supplementary imply parallel sides) so its opposite sides are equal. In practice a rectangle is usually specified by the lengths of its opposite sides, as shown below.

To construct a rectangle, choose a line PQ and mark P and Q distance b apart.
Construct the perpendicular m to PQ at P, and mark S on m, a units from P.
Construct the parallelogram PQRS as before. PQRS is, of course, a rectangle.
The square
- A square is a rectangle with equal sides.
To construct a square with side length a, proceed as for the rectangle.
Constructing translations, rotations and reflections
Congruence is usually defined in terms of translations, rotations and reflections that are the basic isometries or distance preserving transformations of the plane. In this subsection we show how to find the image of the (arbitrary) point P by construction, given the description of the transformation.
A translation T is determined by a pair of points A and B where T maps (or moves) A to B. To find the point Q that T maps P to, simply construct the parallelogram ABQP.
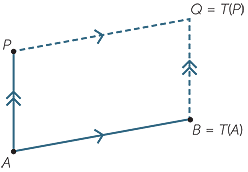
(In some contexts it is said that the translation is determined by the vector ![]() .)
.)
A rotation is determined by a point O called the centre of the rotation and directed
angle α. The rotation maps P to B if POB = α and OP = OB.
POB = α and OP = OB.
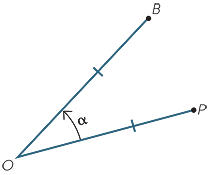
This construction can be performed using ruler and compasses since an angle
can be copied.
A reflection is determined by a line  called the axis of reflection.
called the axis of reflection.
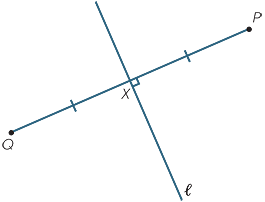
To find the image Q of a point P when reflected in the line  , construct the perpendicular PX to the line
, construct the perpendicular PX to the line  , then produce PX to Q so that PX = XQ.
, then produce PX to Q so that PX = XQ.
Constructing the rational numbers on a number line
We start with a fixed line  and mark two points on it labelled 0 and 1.
and mark two points on it labelled 0 and 1.
Conventionally we draw  horizontal and we mark 0 to the left of 1, but this does not really matter.
horizontal and we mark 0 to the left of 1, but this does not really matter.

Using compasses one can mark all the points 2, 3, 4, … corresponding to the positive integers and the points, −1, −2, −3, … corresponding to the negative integers.
We say ‘we have constructed the integers’.

Suppose we can construct the unit fractions ![]() ,
, ![]() ,
, ![]() ,
, ![]() , … then by using the same construction as above, we can construct all integer multiples of a particular unit fraction. For example, if we can construct
, … then by using the same construction as above, we can construct all integer multiples of a particular unit fraction. For example, if we can construct ![]() then we have
then we have

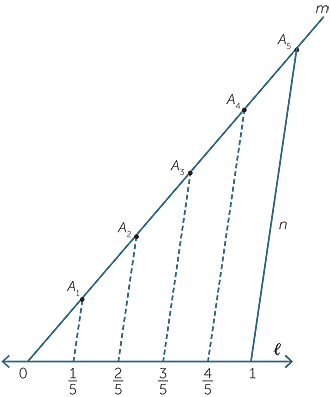 As an example, there is an easy way to construct
As an example, there is an easy way to construct 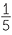 ,
,
 ,
, 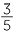 and
and 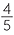 .
.
- Starting with 0 and 1 on
 , draw any line m through 0 (m ≠
, draw any line m through 0 (m ≠  ).
). - Choose a point A1 on m, (A1 ≠ 0).
- With a compass construct equally spaced points 0, A1, A2, A3, A4 and A5 on m.
- Join A5 to 1 − call this line n.
- Finally, construct four lines parallel to n through A1, A2, A3, A4 meeting
 at four points.
at four points.
These points on  are equally spaced, so we have constructed
are equally spaced, so we have constructed ![]() ,
, ![]() ,
, ![]() and
and ![]() on the line
on the line  .
.
We have now, in principle, completed the construction of the rational numbers on the number line  .
.
Exercise 3
Use similar triangles to prove that the points 0, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and 1 are equally spaced on
and 1 are equally spaced on  .
.
By definition a regular polygon is an n-gon ( a polygon with n sides) with all sides equal in length and all angles equal. A regular triangle is an equilateral triangle and a regular quadrilateral is a square, so they both can be constructed using ruler and compasses.
A regular heptagon![]()
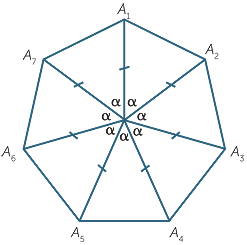
In a regular n-gon each side subtends the angle  at the centre of the n-gon.
at the centre of the n-gon.
For example, with the 7-gon (heptagon) the angle is 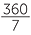 = 51
= 51 °.
°.
The vertices of a regular n-gon lie on a circle. This means that any n-gon can be approximately constructed using a ruler, compasses and protractor. However, it is not possible to construct all n-gons using a ruler and compasses, as we shall discuss in the Links Forward section of this module. (This result would have surprised Euclid.)
As well as the equilateral triangle and the square it is possible to construct a number of other regular polygons including the pentagon, the hexagon, and the octagon. Details are discussed below.
The regular hexagon
There are several interesting ways to construct a regular hexagon. The angle at the centre of a regular hexagon is 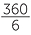 = 60°, thus the hexagon consists of six equilateral triangles. Hence the distance between the six vertices is the same as the radius of the circumcircle.
= 60°, thus the hexagon consists of six equilateral triangles. Hence the distance between the six vertices is the same as the radius of the circumcircle.
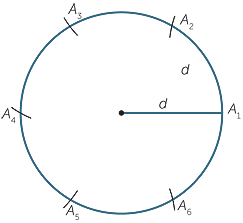 Choose a distance d. Draw a circle of radius d.
Choose a distance d. Draw a circle of radius d.
Choose any point on the circle and mark points
distance d apart using compasses. Then join up
the hexagon.
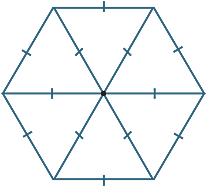 A second construction would be to draw
A second construction would be to draw
six equilateral triangles, as shown in the diagram.
 A third construction is to take an equilateral triangle
A third construction is to take an equilateral triangle
ABC, and bisect the angles at each vertex. These bisectors will be concurrent at the circumcentre of the triangle. Draw the circumcircle. The other three points of the hexagon are where the bisectors meet the circle.
The regular octagon
Given a square it is easy to construct an octagon.

Simply draw in the diagonals of the square and then bisect the angles at the centre.
This gives eight equally spaced points on the circumcircle of the square.
This idea can be generalised so that if you have a regular n-gon then it is easy to construct a regular 2n-gon by bisecting the angles at the centre of the polygon to obtain the other n points on the circle.
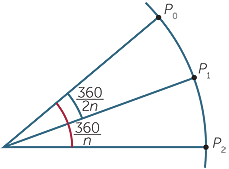
Using the above idea, we can construct regular n-gons for n = 4, 8, 16, 32, … and
for n = 3, 6, 12, 24, …
The regular pentagon
Although extremely interesting, this subsection should be treated as extension material.
Euclid gives a construction for the regular pentagon. The lengths involved include the golden ratio 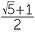 .
.
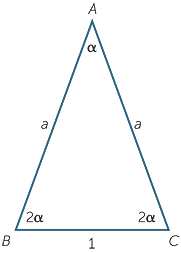 Let α = 36°. The angle at the centre of the
Let α = 36°. The angle at the centre of the
regular pentagon is 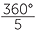 = 72° = 2α.
= 72° = 2α.
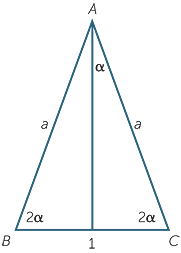
Consider the isosceles triangle ABC with base 1, side length a and angles α, 2α and 2α.
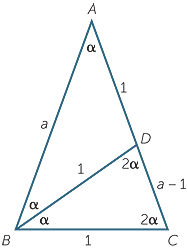 Let D be the point on CA so that BD = 1.
Let D be the point on CA so that BD = 1.  BCD is an isosceles triangle with angles
BCD is an isosceles triangle with angles
α, 2α and 2α. Next  ABD is isosceles so that
ABD is isosceles so that
AD = 1 and DC = a − 1.
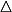 ABC is similar to
ABC is similar to 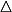 BCD (AAA)
BCD (AAA)
| Thus | 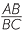 |
= 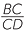 (corresponding sides of similar triangles) (corresponding sides of similar triangles) |
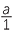 |
=  |
|
| a2 − a | = 1 | |
| a2 − a − 1 | = 0 | |
a |
= 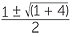 = = 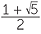 |
|
| But, | a > 0 so, a | = 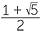 . . |
We can construct ![]() using, for example, a 1, 2,
using, for example, a 1, 2, ![]() right-angled triangle. Hence we can construct 1 +
right-angled triangle. Hence we can construct 1 + ![]() and thence
and thence 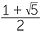 . Finally, we construct a 1, a, a triangle so we have constructed 72° and hence the regular pentagon.
. Finally, we construct a 1, a, a triangle so we have constructed 72° and hence the regular pentagon.
EXERCISE 4
a Describe how to construct regular polygons with 10, 20, 40… sides.
b Describe how to construct a 15-gon and hence 30, 60, 120… -gons.
EXERCISE 5
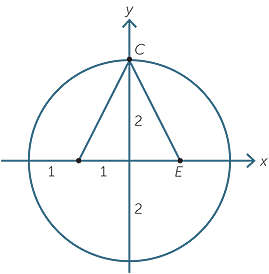 The construction of the regular pentagon given above is somewhat indirect. In this exercise we present a much more direct method but to prove it works does require some trigonometry.
The construction of the regular pentagon given above is somewhat indirect. In this exercise we present a much more direct method but to prove it works does require some trigonometry.
Draw a circle of radius 2 centre the origin.
Let A = (−1, 0) and C = (0, 2). Mark E on the x-axis so that AE = AC and E is to the right of the origin A on the x-axis.
Then CE is the length of the side of a regular pentagon whose vertices lie on the circle.
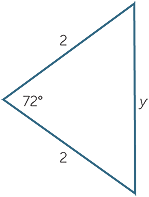 a
a![]() Show CE2 = 10 − 2
Show CE2 = 10 − 2![]()
b![]() From the previous construction, show that cos 72° =
From the previous construction, show that cos 72° = 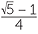 .
.
c![]() Using the cosine rule, or otherwise, show that y2 = 10 − 2
Using the cosine rule, or otherwise, show that y2 = 10 − 2![]() .
.
That is CE is the required length.
Points associated with the triangle
Consider the triangle 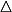 ABC with side lengths a, b and c.
ABC with side lengths a, b and c.
In the following  ABC may be either an acute angled, an obtuse angled or a right-angled triangle. It may be either isosceles or scalene (non-isosceles).
ABC may be either an acute angled, an obtuse angled or a right-angled triangle. It may be either isosceles or scalene (non-isosceles).
There are a large number of points associated with triangle ABC that can be constructed with straight edge and compasses. The most commonly met are:
O![]() the circumcentre
the circumcentre
I![]() the incenter
the incenter
G![]() the centroid
the centroid
H![]() the orthocentre and
the orthocentre and
N![]() the nine-point centre
the nine-point centre
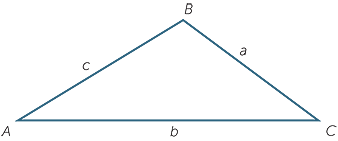
 The circumcircle is the circle which passes through
The circumcircle is the circle which passes through
A, B and C. Its centre O is called the circumcentre
of the triangle. It is constructed as the intersection
of the perpendicular bisectors of the sides of the triangle.
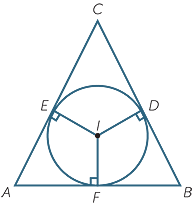 The incircle is the circle tangent to the three sides of
The incircle is the circle tangent to the three sides of
the triangle. Its centre I is called the incentre of the
triangle ABC. To construct I, bisect the angles A and B.
I is where these bisectors meet.
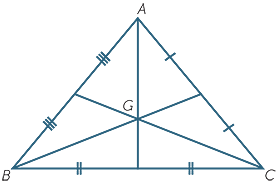 A median of a triangle is the line joining a vertex to the mid-point of the opposite side of the triangle. The centroid is the point G where the medians meet. The construction is clear.
A median of a triangle is the line joining a vertex to the mid-point of the opposite side of the triangle. The centroid is the point G where the medians meet. The construction is clear.
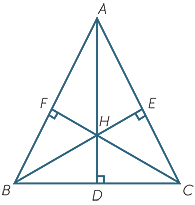 An altitude of a triangle is the line from a vertex perpendicular to the opposite side. The orthocentre is the point H where the altitudes of the triangle meet.
An altitude of a triangle is the line from a vertex perpendicular to the opposite side. The orthocentre is the point H where the altitudes of the triangle meet.
For each of the four constructions given above there is a theorem to be proved. For example, why do the three medians meet? These will all be treated in the module, Congruence and Circle Geometry.
Finally the nine-point circle is the circle that passes through D, E and F in the above diagram.
N is the centre of the circle.
In the eighteenth century Euler proved that H, N, O and G are collinear − a very surprising result.
He also proved that OI2 = R2 − 2rR where R is the radius of the circumcircle and r is the radius of the incircle. These gems of geometry comprehensively destroy the myth that Euclidean geometry is completely dead.
Construction of Square Roots, products and quotients
Construction of Square Roots
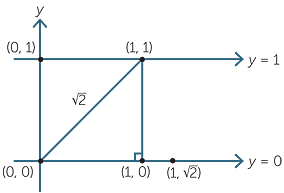
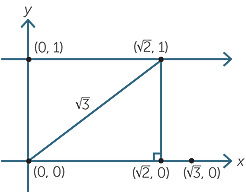
It is possible to construct all square roots of positive integers using right-angled triangles. For example,
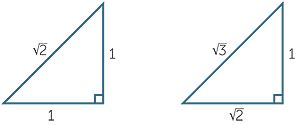
This would be very inefficient for constructing, say, ![]() , but does lead to an interesting classroom exercise presented at the end of this section.
, but does lead to an interesting classroom exercise presented at the end of this section.
It is possible to translate algebraic identities into geometric constructions. For example
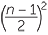 + n =
+ n = 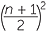
means that there is a right-angled triangle with side lengths 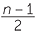 ,
, ![]() ,
, 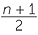 and given that we have constructed the rationals, we can now construct
and given that we have constructed the rationals, we can now construct ![]() in one step.
in one step.
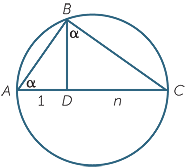 The next construction depends on the well-known fact from
The next construction depends on the well-known fact from
circle geometry that the angle in a semi-circle is a right angle.
Begin with a circle of diameter n + 1 and draw the perpendicular BD dividing the diameter in the ratio one to n.
Since ABC is a right angle, we have three similar triangles. In particular,
ABC is a right angle, we have three similar triangles. In particular, 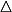 ADB is similar to
ADB is similar to 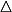 BDC (AAA)
BDC (AAA)
so 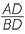 =
=  (corresponding sides of similar triangles).
(corresponding sides of similar triangles).
BD2 = AD.DC = 1.n = n and BD = 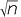
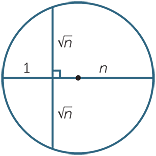 Hence, we have in a circle of diameter n + 1 a simple construction for the square root of the positive integer n.
Hence, we have in a circle of diameter n + 1 a simple construction for the square root of the positive integer n.
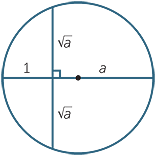 Indeed if a is a constructible (with ruler and compasses) real number then so is
Indeed if a is a constructible (with ruler and compasses) real number then so is 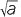 .
.
Finally, we consider a very important generalisation of the above result.

Theorem
Suppose two chords of a circle meet inside the circle, cutting off lengths a, b, c and d as shown. Then ab = cd.
Proof
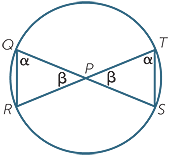 Join QS and TR.
Join QS and TR.
![]() SQR = ∠STR (angles in the same segment)
SQR = ∠STR (angles in the same segment)
Hence 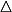 STP is similar to
STP is similar to 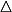 RQP (AAA)
RQP (AAA)
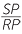 =
= 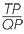 (corresponding sides of similar triangles)
(corresponding sides of similar triangles)
QP.PS = TP.PR and the theorem is proved.
Notes
- 1
- This theorem includes the result for constructing the square root as given above.
- 2
- If d = 1 then c = ab so if a and b are constructible (with ruler and compasses) so is their product.
Also a =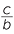 so if c and b are constructible, then so is their quotient.
so if c and b are constructible, then so is their quotient.
We finish with an exercise which shows how, in principle, to construct sequentially on a number line 1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() …
…
EXERCISE 6
With ruler and compasses construct the above diagram.
With a compass mark (![]() , 0)
, 0)
Mark (![]() , 1). With a compass mark (
, 1). With a compass mark (![]() , 0).
, 0).
Repeat the construction to obtain ((![]() , 0), (
, 0), (![]() , 0)), …
, 0)), …
The limits to construction using ruler and compass
As indicated within the content and links forward sections Greek mathematicians were interested in general construction questions such as construction using straight edge and compasses.
As we showed above, they knew that all rational lengths could be constructed as could radical expressions involving square roots such as ![]() −
− ![]() .
.
Incidentally, we have proved ![]() ,
, ![]() ,
, ![]() … are all constructible.
… are all constructible.
There are three famous constructions that the Greeks could not perform.
Duplication of the cube
This asked for a construction of a cube twice the volume of a given cube. That is, for a construction of ![]() .
.
Trisection of an angle
This asked for a construction of an angle one third of the size of a given angle.

This would have, for example, constructed the regular 9-gon (or nonagon).
Quadrature of the circle
This asked for a construction of a square equal in area to a given circle. That is, for a construction of π or perhaps ![]() .
.
Despite the fact that the only regular polygons that were known to be constructible
(using straight edge and compasses) were those with 2a, 3.2a, 5.2a and 15.2a, the Greeks were seeking methods for constructing the 7-gon, the 9-gon, the 11-gon etc. Indeed, it was so important that Archimedes considered such problems and found a construction for a heptagon (7-gon) using a tool other than the straight edge and compasses.
It is not surprising that the Greeks found these constructions so difficult since they are impossible! It is very likely that no Greek mathematician thought of this possibility.
In the 19th century two mathematicians, Abel and Galois, developed the ideas to prove these results and many others. For example, Abel proved that there was no formula for solving a fifth degree polynomial, a quintic, in contrast to the well-known formulas for the quadratic (approximately 2000 BC), the cubic (approximately 1500 AD) and the quartic (approximately 1500 AD).
The key idea in Galois theory, as it is called, is to study the polynomials satisfied by numbers not the numbers themselves. For example, ![]() satisfies x2 − 2 and
satisfies x2 − 2 and ![]() (which is the key to duplicating a cube) satisfies x3 − 2.
(which is the key to duplicating a cube) satisfies x3 − 2.
π does not satisfy any polynomial with integer coefficients − it is called transcendental.
Trisecting an angle also corresponds to solving a cubic.
The main theorem on constructability is that only numbers such as ![]() −
− ![]() can be constructed with ruler and compasses. This only really depends on the fact that the equations for lines and circles are of degree 1 and 2 (in terms of the coordinates x and y).
can be constructed with ruler and compasses. This only really depends on the fact that the equations for lines and circles are of degree 1 and 2 (in terms of the coordinates x and y).
The theorem implies that the three classical construction cannot be carried out.
Regular Polygons
At the age of about fifteen, Gauss (1777-1855) discovered how to construct a regular 17-gon using straight edge and compasses. The story is told that this success convinced Gauss to become a professional mathematician. The reason why this was possible is that
![]() 17= 24 + 1 = 222 + 1
17= 24 + 1 = 222 + 1
a so-called Fermat prime. If we let
![]() Fn = 22n + 1
Fn = 22n + 1
then the only known Fermat primes are F0 = 3, F1 = 5, F2 = 17, F3 = 257 and F4 = 65 537. As of March 2010, only F0 to F11 have been completely factored.
The theorem from Galois theory is that a regular n-gon, n odd, is constructible if and only if n is a product of distinct Fermat primes.
This means that the Greek search for straight edge and compasses constructions of the 7-gon, 11-gon and 13-gon was doomed to failure.
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
History of Mathematics, D. E. Smith, Dover publications New York, (1958)
EXERCISE 1
Triangle ABC is not right-angled as 62 + 52 ≠ 64
EXERCISE 3
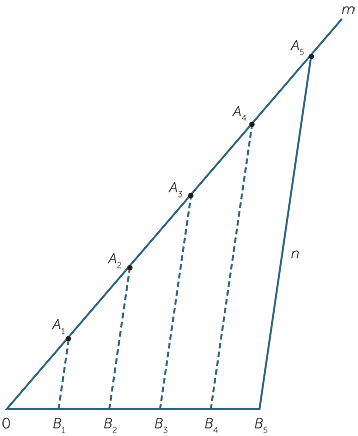
Triangles OA1B1, OA2B2, OA3B3, OA4B4, OA5B5 are all similar (AA).
Since OB2 = 2 OB1, OB1 = B1B2.
Continuing this argument shows that the markers are equally spaced.
EXERCISE 4
- a
- Draw a regular pentagon circumscribed in a circle centre O.
Draw lines from centre O through the midpoint of each side of the pentagon and mark where each line meets the circle again.
These points together with the vertices of the pentagon are the vertices of the dodecagon
(10 − sided polygon).
The other polygons are formed in a similar way. - b
- Draw a regular pentagon circumscribed in a circle centre O. Draw the equilateral triangle inscribed in this circle sharing one vertex with the pentagon.
The difference in the angles (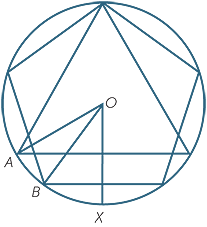
 AOX −
AOX − BOX) is 60° − 36° = 24°
BOX) is 60° − 36° = 24°
The 15 − gon can be constructed and the others listed can be constructed using the techniques outlined in part a.
EXERCISE 5
a![]() AC =
AC = ![]() and therefore AE =
and therefore AE = ![]() − 1. Use Pythagoras’ theorem to find CE.
− 1. Use Pythagoras’ theorem to find CE.
b![]() From the diagram, α = 36° and 2α = 72°. It was found that a =
From the diagram, α = 36° and 2α = 72°. It was found that a = 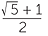
![]() cos 2α =
cos 2α = 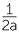 =
= 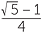
| c | y2 | = 4 + 4 − 2 × 2 × 2 cos 72o | |
= 8 − 8 × 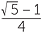 |
|||
| = 8 − 2 |
|||
| = 10 − 2 |
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


