The Improving Mathematics Education in Schools (TIMES) Project
The Improving Mathematics Education in Schools (TIMES) Project
Most geometry so far has involved triangles and quadrilaterals, which are formed by intervals on lines, and we turn now to the geometry of circles. Lines and circles are the most elementary figures of geometry − a line is the locus of a point moving in a constant direction, and a circle is the locus of a point moving at a constant distance from some fixed point − and all our constructions are done by drawing lines with a straight edge and circles with compasses. Tangents are introduced in this module, and later tangents become the basis of differentiation in calculus.
The theorems of circle geometry are not intuitively obvious to the student, in fact most people are quite surprised by the results when they first see them. They clearly need to be proven carefully, and the cleverness of the methods of proof developed in earlier modules is clearly displayed in this module. The logic becomes more involved − division into cases is often required, and results from different parts of previous geometry modules are often brought together within the one proof. Students traditionally learn a greater respect and appreciation of the methods of mathematics from their study of this imaginative geometric material.
The theoretical importance of circles is reflected in the amazing number and variety of situations in science where circles are used to model physical phenomena. Circles are the first approximation to the orbits of planets and of their moons, to the movement of electrons in an atom, to the motion of a vehicle around a curve in the road, and to the shapes of cyclones and galaxies. Spheres and cylinders are the first approximation of the shape of planets and stars, of the trunks of trees, of an exploding fireball, and of a drop of water, and of manufactured objects such as wires, pipes, ball-bearings, balloons, pies and wheels.
We begin by recapitulating the definition of a circle and the terminology used for circles. Throughout this module, all geometry is assumed to be within a fixed plane.
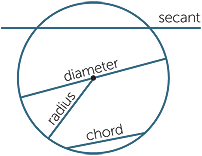 Any interval joining a point on the circle to the centre is called a radius. By the definition of a circle, any two radii have the same length. Notice that the word ‘radius’ is being used to refer both to these intervals and to the common length of these intervals.
Any interval joining a point on the circle to the centre is called a radius. By the definition of a circle, any two radii have the same length. Notice that the word ‘radius’ is being used to refer both to these intervals and to the common length of these intervals.Symmetries of a circle
Circles have an abundance of symmetries:
 A circle has every possible rotation symmetry about its centre, in that every rotation of the circle about its
A circle has every possible rotation symmetry about its centre, in that every rotation of the circle about its If AOB is a diameter of a circle with centre O, then the
If AOB is a diameter of a circle with centre O, then theAs a result of these symmetries, any point P on a circle
can be moved to any other point Q on the circle. This can
be done by a rotation through the angle θ =  POQ about
POQ about
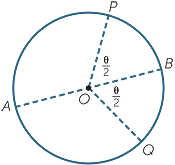 the centre. It can also be done by a reflection in the diameter
the centre. It can also be done by a reflection in the diameter
AOB bisecting  POQ. Thus every point on a circle is essentially
POQ. Thus every point on a circle is essentially
the same as every other point on the circle − no other figure in
the plane has this property except for lines.
EXERCISE 1
 Identify all translations, rotations and reflections of the plane that map a line
Identify all translations, rotations and reflections of the plane that map a line  onto itself.
onto itself. Which of the transformations in part a map a particular point P on
Which of the transformations in part a map a particular point P on  to another particular point Q on
to another particular point Q on  .
.Congruence and similarity of circles
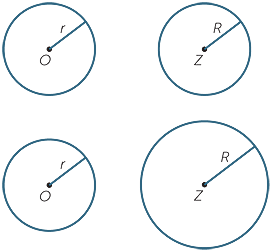 Any two circles with the same radius are congruent− if one circle is moved so that its centre coincides with the centre of the other circle, then it follows from the definition that the two circles will coincide.
Any two circles with the same radius are congruent− if one circle is moved so that its centre coincides with the centre of the other circle, then it follows from the definition that the two circles will coincide.
More generally, any two circles are similar − move one circle so that its centre coincides with the centre of the other circle, then apply an appropriate enlargement so that it coincides exactly with the second circle.
A circle forms a curve with a definite length, called the circumference, and it encloses a definite area. The similarity of any two circles is the basis of the definition of π, the ratio of the circumference and the diameter of any circle. We saw in the module, The Circles that if a circle has radius r, then
circumference of the circle = 2πr and area of the circle = πr2
Radii and chords
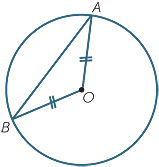 Let AB be a chord of a circle not passing through its
Let AB be a chord of a circle not passing through its
centre O. The chord and the two equal radii OA and
BO form an isosceles triangle whose base is the chord.
The angle  AOB is called the angle at the centre
AOB is called the angle at the centre
subtended by the chord.
In the module, Rhombuses, Kites and Trapezia we discussed the axis of symmetry
of an isosceles triangle. Translating that result into the language of circles:
Theorem
Let AB be a chord of a circle with centre O. The following three lines coincide:
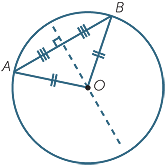 The bisector of the angle
The bisector of the angle  AOB at the centre subtended by the chord.
AOB at the centre subtended by the chord.Trigonometry and chords
Constructions with radii and chords give plenty of opportunity for using trigonometry.
EXERCISE 2
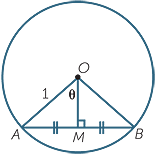 In the diagram to the right, the interval AM subtends an angle θ
In the diagram to the right, the interval AM subtends an angle θ
at the centre O of a circle of radius 1. Show that:
a ![]() AM = sin θ
AM = sin θ ![]() b
b ![]() OM = cos θ
OM = cos θ
This exercise shows that sine can be regarded as the length of the semichord AM in a circle of radius 1, and cosine as the perpendicular distance of the chord from the centre. Until modern times, tables of sines were compiled as tables of chords or semichords, and the name ‘sine’ is conjectured to have come in a complicated and confused way from the Indian word for semichord.
Arcs and sectors
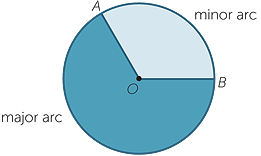 Let A and B be two different points on a circle with centre O. These two points divide the circle into two opposite arcs. If the chord AB is a diameter, then the two arcs are called semicircles. Otherwise, one arc is longer than the other − the longer arc is called the major arc AB and the shorter arc is called the minor arc AB.
Let A and B be two different points on a circle with centre O. These two points divide the circle into two opposite arcs. If the chord AB is a diameter, then the two arcs are called semicircles. Otherwise, one arc is longer than the other − the longer arc is called the major arc AB and the shorter arc is called the minor arc AB.
Now join the radii OA and OB. The reflex angle  AOB is called the angle subtended by the major arc AB. The non-reflex angle
AOB is called the angle subtended by the major arc AB. The non-reflex angle  AOB is called the angle subtended by the minor arc AB, and is also the angle subtended by the chord AB.
AOB is called the angle subtended by the minor arc AB, and is also the angle subtended by the chord AB.
The two radii divide the circle into two sectors, called correspondingly the major sector OAB and the minor sector OAB.
It is no surprise that equal chords and equal arcs both subtend equal angles at the centre of a fixed circle. The result for chords can be proven using congruent triangles, but congruent triangles cannot be used for arcs because they are not straight lines, so we need to identify the transformation involved.
Theorem
Proof
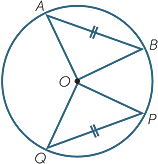 In the diagram to the right,
In the diagram to the right,  AOB
AOB 
 POQ (SSS)
POQ (SSS) AOB =
AOB =  POQ (matching angles of congruent
POQ (matching angles of congruent POQ and
POQ and  AOB coincide,
AOB coincide,Segments
A chord AB of a circle divides the circle into two segments. If AB is a diameter, the two congruent segments are called semicircles − the word ‘semicircle’ is thus used both for the semicircular arc, and for the segment enclosed by the arc and the diameter. Otherwise, the two segments are called a major segment and a minor segment.
The word ‘subtend’
The word ‘subtend’ literally means ‘holds under’, and is often used in geometry to describe an angle.
Suppose that we have an interval or arc AB and a point P not on AB. Join the intervals AP and BP to form the angle  APB. We say that the angle
APB. We say that the angle  APB is the angle subtended by the interval or arc AB at the point P.
APB is the angle subtended by the interval or arc AB at the point P.
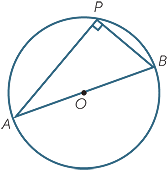 Let AOB be a diameter of a circle with centre O, and let P be any other point on the circle. The angle
Let AOB be a diameter of a circle with centre O, and let P be any other point on the circle. The angle  APB subtended at P by the diameter AB is called an angle in a semicircle. This angle
APB subtended at P by the diameter AB is called an angle in a semicircle. This angle
is always a right angle − a fact that surprises most people when they see the result for the first time.
Theorem
An angle in a semicircle is a right angle.
Proof
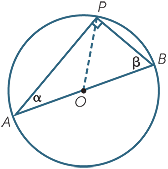 Let AB be a diameter of a circle with centre O,
Let AB be a diameter of a circle with centre O,
and let P be any other point on the circle.
Join the radius PO, and let α =  A and β =
A and β =  B.
B.
The triangles AOP and BOP are isosceles because all radii are equal, so  APO = α and
APO = α and  BPO = β (base angles of isosceles triangles AOP and BOP).
BPO = β (base angles of isosceles triangles AOP and BOP).
Hence α + β + (α + β ) = 180° (angle sum of  APB)
APB)
| 2α + 2β | = 180° | ||
| α+ β | = 90°, | ||
| so |  APB APB |
= 90°, as required. |
This famous theorem is traditionally ascribed to the Greek mathematician Thales, the first known Greek mathematician.
EXERCISE 3
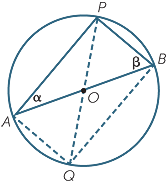 Thales’ theorem can also be proven using the following test for a rectangle developed in the module, Parallelograms and Rectangles.
Thales’ theorem can also be proven using the following test for a rectangle developed in the module, Parallelograms and Rectangles.
A quadrilateral whose diagonals are equal and bisect each other is a rectangle.
Join the radius PO and produce it to a diameter POQ, then join up the quadrilateral APBQ. Explain why  APB is a right angle.
APB is a right angle.
Constructing a right angle at the endpoint of an interval
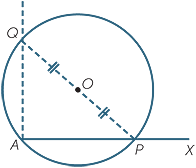 Thales’ theorem gives a quick way to construct a right
Thales’ theorem gives a quick way to construct a right
angle at the endpoint of an interval AX.
 PAQ = 90°.
PAQ = 90°.The converse theorem
The angle in a semicircle theorem has a straightforward converse that is best expressed as a property of a right-angled triangle:
Theorem
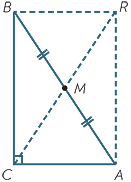 The circle whose diameter is the hypotenuse of a right-angled
The circle whose diameter is the hypotenuse of a right-angled
triangle passes through all three vertices of the triangle.
Proof
Let  ABC be right-angled at C, and let M be the midpoint of
ABC be right-angled at C, and let M be the midpoint of
the hypotenuse AB.
We need to prove that MC = MA = MB. Complete the rectangle ACBR. Because ACBR is a rectangle, its diagonals bisect each other and are equal. Hence M is the midpoint of the other diagonal CR, and AM = BM = CM = RM .
This is an excellent example of the way ideas in geometry fit together − a significant theorem about circles has been proven using a property of rectangles.
Two practical situations to illustrate the converse theorem
A set of points in the plane is often called a locus. The term is used particularly when the set of points is the curve traced out by a moving point. For example, a circle can be defined as the locus of a point that moves so that its distance from some fixed point is constant. The two examples below use the converse of the angle in a semicircle theorem to describe a locus.
EXERCISE 4
 A photographer is photographing the ornamental front
A photographer is photographing the ornamental front
of a building. He wants the two ends of the front to
subtend a right angle at his camera. Describe the set
of all positions where he can stand.
EXERCISE 5
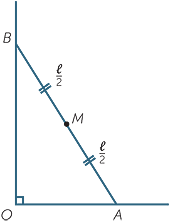 A plank of length
A plank of length  metres is initially resting flush against a wall, but it slips outwards, with its top sliding down the wall and its foot moving at right angles to the wall. What path does the midpoint of the plank trace out?
metres is initially resting flush against a wall, but it slips outwards, with its top sliding down the wall and its foot moving at right angles to the wall. What path does the midpoint of the plank trace out?
Angles at the centre and circumference
The angle-in-a-semicircle theorem can be generalised considerably. In each diagram below, AB is an arc of a circle with centre O, and P is a point on the opposite arc. The arc AB subtends the angle  AOB at the centre. The arc also subtends the angle
AOB at the centre. The arc also subtends the angle  APB, called an angle at the circumference subtended by the arc AB.
APB, called an angle at the circumference subtended by the arc AB.
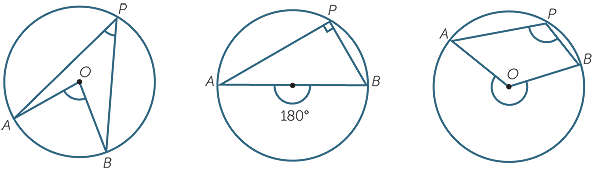
In the middle diagram, where the arc is a semicircle, the angle at the centre is a straight angle, and by the previous theorem, the angle at the circumference is a right angle − exactly half. We shall show that this relationship holds also for the other two cases, when the arc is a minor arc (left-hand diagram) or a major arc (right-hand diagram). The proof uses isosceles triangles in a similar way to the proof of Thales’ theorem.
Theorem
An angle at the circumference of a circle is half the angle at the centre subtended by the same arc.
Proof
Let AB be an arc of a circle with centre O, and let P be any point on the opposite arc. We need to prove  AOB = 2
AOB = 2 APB. The proof divides into three cases, depending on whether:
APB. The proof divides into three cases, depending on whether:
Case 1: O lies inside  ABP
ABP ![]() Case 2: O lies on
Case 2: O lies on  APB
APB ![]() Case 3: O lies outside
Case 3: O lies outside  APB.
APB.
![]()
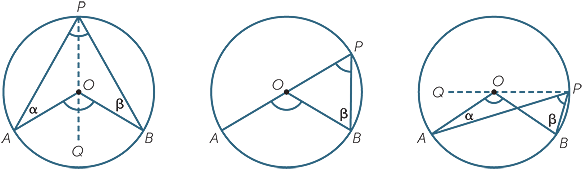
Case 1: Join PO and produce PO to Q. Then OA = OB = OP (radii), so we have two isosceles triangles OAP and OAQ.
| Let |  OAP OAP |
= α and  OBP = β. OBP = β. |
|||
| Then |  APO APO |
= α | (base angles of isosceles  OAP) OAP) |
||
| and |  BPO BPO |
= β | (base angles of isosceles  OBP). OBP). |
||
| Hence |  AOQ AOQ |
= 2α | (exterior angle of  OAP) OAP) |
||
| and |  BOQ BOQ |
= 2β | (exterior angle of  OBP), OBP), |
||
 AOB AOB |
= 2α + 2β = 2(α + β) = 2 ×  APB. APB. |
||||
EXERCISE 6
Complete the proof in the other two cases.
EXAMPLE
A punter stands on the edge of a circular racing track. With his binoculars he is following a horse that is galloping around the track at one revolution a minute. Explain why the punter’s binoculars are rotating at a constant rate of half a revolution per minute.
Solution
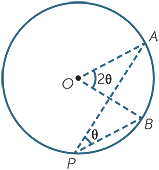 As the horse moves from position A to position B, the horse moves an angle
As the horse moves from position A to position B, the horse moves an angle  AOB = 2θ about the centre O of the track.
AOB = 2θ about the centre O of the track.
The angle at the circumference is half the angle at the centre,
so  APB = θ which means that the punter’s binoculars rotate by an angle θ the horse moves from A to B. Hence the punter is rotating his binoculars at a constant rate that is half the rate at which the horse is rotating about the centre.
APB = θ which means that the punter’s binoculars rotate by an angle θ the horse moves from A to B. Hence the punter is rotating his binoculars at a constant rate that is half the rate at which the horse is rotating about the centre.
Angles subtended by the same arc
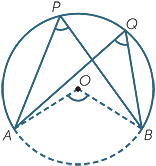 In the diagram to the right, the two angles
In the diagram to the right, the two angles  APB and
APB and  AQB
AQB
are subtended by the same (minor) arc AB. Each angle is half
the angle  AOB at the centre subtended by the same arc,
AOB at the centre subtended by the same arc,
so  APB =
APB =  AQB.
AQB.
This corollary of the previous theorem is a particularly significant
result about angles in circles:
Theorem
Two angles at the circumference subtended by the same arc are equal.
Thales’ theorem is a special case of this theorem.
Some alternative terminology
The last two theorems are often expressed in slightly different language, and some explanation is needed to avoid confusion.
In the context of these two theorems, it is best to avoid the phrases ‘standing on a chord AB’ and ‘subtended by a chord AB′, because we need to distinguish between angles subtended by the major arc AB and angles subtended by the minor arc AB.
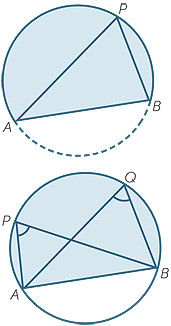 In the upper diagram to the right, the angle
In the upper diagram to the right, the angle  APB is called
APB is calledExtension − The orthocentre of a triangle
An altitude of a triangle is a perpendicular from any of the three vertices to the opposite side, produced if necessary. The two cases are illustrated in the diagrams below.

There are three altitudes in a triangle. The following theorem proves that they concurrent at a point called the orthocentre H of the triangle. It is surprising that circles can be used to prove the concurrence of the altitudes.
Theorem
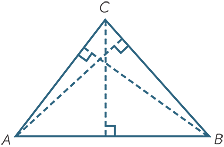 The altitudes of a triangle are concurrent.
The altitudes of a triangle are concurrent.
EXERCISE 7
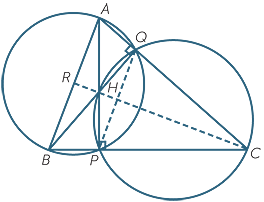 In the diagram to the right, the altitudes AP and
In the diagram to the right, the altitudes AP and
BQ meet at H. The interval CH is produced to meet AB , produced if necessary, at R. We need to prove that CR ⊥ AB.
 QCH =
QCH =  QPH.
QPH. APQ =
APQ =  ABQ.
ABQ. ABQ and
ABQ and  ACR to explain why CR ⊥ AB.
ACR to explain why CR ⊥ AB.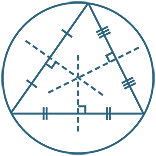 In the module, Congruence, we showed how to draw the circumcircle through the vertices of any triangle. To do this, we showed that the perpendicular bisectors of its three sides are concurrent, and that their intersection, called the circumcentre of the triangle, is equidistant from each vertex.
In the module, Congruence, we showed how to draw the circumcircle through the vertices of any triangle. To do this, we showed that the perpendicular bisectors of its three sides are concurrent, and that their intersection, called the circumcentre of the triangle, is equidistant from each vertex.
 No other circle passes through these three vertices. If we tried to take as centre a point P other than the circumcentre, then P would not lie on one of the perpendicular bisectors, so it could not be equidistant from the three vertices.
No other circle passes through these three vertices. If we tried to take as centre a point P other than the circumcentre, then P would not lie on one of the perpendicular bisectors, so it could not be equidistant from the three vertices.
When there are four points, we can always draw a circle through any three of them (provided they are not collinear), but only in special cases will that circle pass through the fourth point. A cyclic quadrilateral is a quadrilateral whose vertices all lie on a circle. This is the last type of special quadrilateral that we shall consider.
Constructing the circumcircle of a cyclic quadrilateral
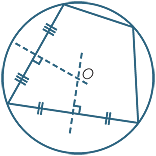 Suppose that we are given a quadrilateral that is known to be
Suppose that we are given a quadrilateral that is known to be
cyclic, but whose circumcentre is not shown (perhaps it has been rubbed out). The circumcentre of the quadrilateral is the circumcentre of the triangle formed by any three of its vertices, so the construction to the right will find its circumcentre.
The opposite angles of a cyclic quadrilateral
The distinctive property of a cyclic quadrilateral is that its opposite angles are supplementary. The following proof uses the theorem that an angle at the circumference is half the angle at the centre standing on the same arc.
Theorem
The opposite angles of a cyclic quadrilateral are supplementary.
Proof
Let ABCD be a cyclic quadrilateral with O the centre of the circle.
Join the radii OB and OD. Let α and g be the angles at the centre, as shown on the diagram.
| Then | α+ γ | = 360° | (angles in a revolution at O) | 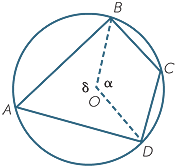 |
||
| Also |  A A |
=  α α |
(angles on the same arc BCD) | |||
| and |  C C |
=  γ γ |
(angles on the same arc BAD) | |||
| so |  A + A +  C C |
=  α + α +  γ= 180° γ= 180° |
||||
Hence also  ABC + ABC +  ADC = 180° (angle sum of quadrilateral ABCD) ADC = 180° (angle sum of quadrilateral ABCD) |
||||||
Here is an alternative proof using the fact that two angles in the same segment are equal.
EXERCISE 8
Join the diagonals AC and BD of the cyclic quadrilateral ABCD. Let α, β, γ and δ be the angles shown.
 DBC = α
DBC = α
Exterior angles of a cyclic quadrilateral
An exterior angle of a cyclic quadrilateral is supplementary to the adjacent interior angle, so is equal to the opposite interior angle. This gives us the corollary to the cyclic quadrilateral theorem:
Theorem
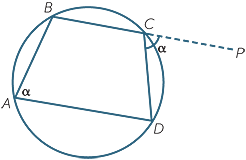 An exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
An exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
Proof
In the diagram to the right, BC is produced to P to form the exterior angle  PCD. This exterior angle and
PCD. This exterior angle and  A are both supplementary to
A are both supplementary to  BCD, so they are equal.
BCD, so they are equal.
EXERCISE 9
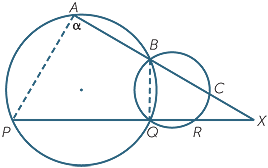 Show that AP || CR in the diagram to the right.
Show that AP || CR in the diagram to the right.
EXERCISE 10
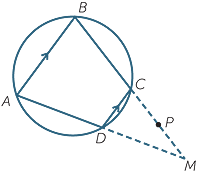 If a cyclic trapezium is not a rectangle, show that the other two sides are not parallel, but have equal length.
If a cyclic trapezium is not a rectangle, show that the other two sides are not parallel, but have equal length.
Extension − A test for a cyclic quadrilateral
The property of a cyclic quadrilateral proven earlier, that its opposite angles are supplementary, is also a test for a quadrilateral to be cyclic. That is the converse is true. This theorem completes the structure that we have been following − for each special quadrilateral, we establish its distinctive properties, and then establish tests for it.
The proof uses ‘proof by contradiction’, and is thus a little more difficult than other
Year 10 material.
Theorem
If the opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
Proof
Let ABCD be a quadrilateral with  A +
A + C = 180°.
C = 180°.
Construct the circle through A, B and D, and suppose, by way of contradiction, that the circle does not pass through C.
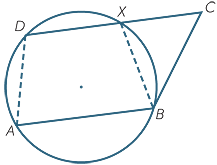 Let DC, produced if necessary, meet the circle again at X, and join XB.
Let DC, produced if necessary, meet the circle again at X, and join XB.
Then  A and
A and  BXD are supplementary because ABXD is a cyclic quadrilateral,
BXD are supplementary because ABXD is a cyclic quadrilateral,
so the angles  DXB and
DXB and  DCB are equal,
DCB are equal,
so XB || CB
Hence XB and CB are the same line, so C and X coincide, that is the circle does pass through C.
EXERCISE 11
Prove the following alternative form of the above theorem:
If an exterior angle of a quadrilateral equals the opposite interior angle, then the quadrilateral is cyclic.
EXERCISE 12
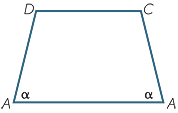 In the diagram to the right, the two adjacent acute angles of
In the diagram to the right, the two adjacent acute angles of
the trapezium are equal.
Prove that the trapezium is cyclic.
Extension − The sine rule and circle geometry
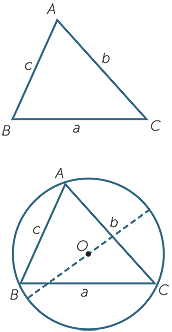 The sine rule states that for any triangle ABC, the ratio
The sine rule states that for any triangle ABC, the ratio
of any side over the sine of its opposite angle is a constant,
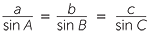
Each term is the ratio of a length over a pure number, so their common value seems to be a length. Thus it reasonable to ask, what is this common length? The answer is a surprise − the common length is the diameter of the circumcircle through
the vertices of the triangle.
The proof of this result provides a proof of the sine rule
that is independent of the proof given in the module,
Further Trigonometry.
Theorem
In any triangle ABC,  =
= 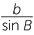 =
=  = 2R, where R is the radius of the circumcircle.
= 2R, where R is the radius of the circumcircle.
Proof
Let O be the centre of the circumcircle through A, B and C, and let  A = α.
A = α.
It is sufficient to prove that  is the diameter of the circumcircle.
is the diameter of the circumcircle.
There are three cases, as shown below.
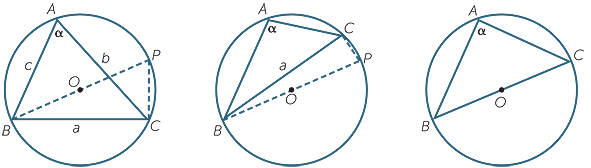
| Case 1: A and O lie onthe same side of BC. | Case 2: A and O lie on opposite sides of BC. | Case 3: O lies on BC |
In cases 1 and 2, construct the diameter BOP, and join PC .
EXERCISE 13
a ![]() Complete the following steps of the proof in Case 1.
Complete the following steps of the proof in Case 1.
i ![]() Explain why
Explain why  BCP = 90° and
BCP = 90° and  P =α
P =α
ii![]() Complete the proof using
Complete the proof using  BCP.
BCP.
b ![]() Complete the following steps of the proof in Case 2.
Complete the following steps of the proof in Case 2.
i ![]() Explain why
Explain why  BCP = 90° and sin P = sinα
BCP = 90° and sin P = sinα
ii![]() Complete the proof using
Complete the proof using  BCP.
BCP.
c ![]() Complete the proof in Case 3.
Complete the proof in Case 3.
Tangents to circles
A tangent to a circle is a line that meets the circle at just one point. The diagram below shows that given a line and a circle, can arise three possibilities:
The words ‘secant’ and ‘tangent’ are from Latin − ‘secant’ means ‘cutting’ (as in ‘cross-section’), and ‘tangent’ means ‘touching’ (as in ‘tango’).

The point where a tangent touches a circle is called a point of contact. It is not immediately obvious how to draw a tangent at a particular point on a circle, or even whether there may be more than one tangent at that point. The following theorem makes the situation clear, and uses Pythagoras’ theorem in its proof.
Theorem
Let T be a point on a circle with centre O.
Proof
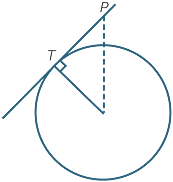 First we prove parts a and c. Let
First we prove parts a and c. Let  be the line through T perpendicular to the radius OT. Let P be any other point on
be the line through T perpendicular to the radius OT. Let P be any other point on  , and join the interval OP. Then using Pythagoras’ theorem in
, and join the interval OP. Then using Pythagoras’ theorem in  OTP,
OTP,
![]() OP2 = OT2 + PT2; which is greater than OT2,
OP2 = OT2 + PT2; which is greater than OT2,
so OP is greater than the radius OT. Hence P lies outside the circle, and not on it. This proves that the line  is a tangent, because it meets the circle only at T. It also proves that every point on
is a tangent, because it meets the circle only at T. It also proves that every point on  , except for T, lies outside the circle.
, except for T, lies outside the circle.
It remains to prove part b, that there is no other tangent
to the circle at T.
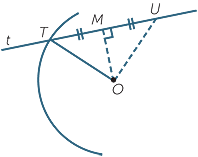 Let t be a tangent at T, and suppose, by way of contradiction, that t were not perpendicular to OT. Let M be the foot of the perpendicular from O to t, and construct the point U on t,on the other side of M, so that UM = MT. Then using Pythagoras’ theorem in
Let t be a tangent at T, and suppose, by way of contradiction, that t were not perpendicular to OT. Let M be the foot of the perpendicular from O to t, and construct the point U on t,on the other side of M, so that UM = MT. Then using Pythagoras’ theorem in  OMT and
OMT and  OMU,
OMU,
![]() OT2 = OM2 + MT2 = OM2 + MU2 = OU2,
OT2 = OM2 + MT2 = OM2 + MU2 = OU2,
So OU = OT. Hence U also lies on the circle, contradicting the fact that t is a tangent.
Construction − Tangents from an external point
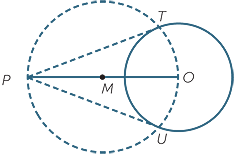 Using this radius and tangent theorem, and the
Using this radius and tangent theorem, and the
angle in a semi circle theorem, we can now construct
tangents to a circle with centre O from a point P outside
the circle.
The angles  PTO and
PTO and  PUO are right angles, because they are angles in a semicircle. Hence the lines PT and PU are tangents, because they are perpendicular to the radii OT and OU, respectively.
PUO are right angles, because they are angles in a semicircle. Hence the lines PT and PU are tangents, because they are perpendicular to the radii OT and OU, respectively.
Tangents from an external point have equal length
It is also a simple consequence of the radius-and-tangent theorem that the two tangents PT and PU have equal length.
Notice that here, and elsewhere, we are using the word ‘tangent’ in a second sense, to mean not the whole line, but just the interval from an external point to the point
of contact.
Theorem
Tangents to a circle from an external point have equal length.
EXERCISE 14
Prove this result using either congruence or Pythagoras’ theorem.
Tangents and trigonometry
The right angle formed by a radius and tangent gives further opportunities for simple trigonometry. The following exercise shows how the names ‘tangent’ and ‘secant’, and their abbreviations tan θ and sec θ, came to be used in trigonometry. In a circle of radius 1, the length of a tangent subtending an angle θ at the centre is tan θ , and the length of the secant from the external point to the centre is sec θ .
EXERCISE 15
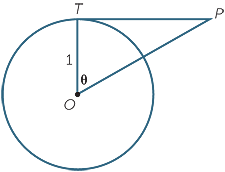 A tangent PT to a circle of radius 1 touches the circle
A tangent PT to a circle of radius 1 touches the circle
at T and subtends an angle θ at the centre O. Show that
![]() PT = tan θ and PO = sec θ
PT = tan θ and PO = sec θ
where the trigonometry function secant is defined
by sec θ = 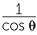 .
.
Quadrilaterals with incircles
The following exercise involves quadrilaterals within which an incircle can be drawn tangent to all four sides. These quadrilaterals form yet another class of special quadrilaterals.
EXERCISE 16
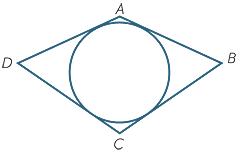 The sides of a quadrilateral are tangent to a circle
The sides of a quadrilateral are tangent to a circle
drawn inside it. Show that the sums of opposite sides of the quadrilateral are equal.
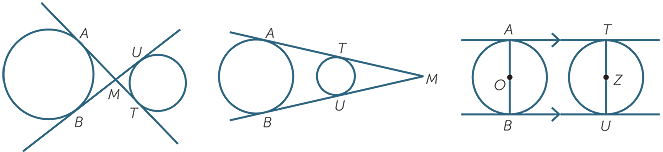
Common tangents and touching circles
A line that is tangent to two circles is called a common tangent to the circles. When the points of contact are distinct, there are two cases, as in the diagrams below. The two circles lie on the same side of a direct common tangent, and lie on opposite sides of an indirect common tangent.
 |
 |
|
| Direct common tangent | Indirect common tangent |
Two circles are said to touch at a common point T if there is a common tangent to both circles at the point T. As in the diagram below, the circles touch externally when they are on opposite sides of the common tangent, and touch internally when they are on the same side of the common tangent.

Provided that they are distinct, touching circles have only the one point in common.
EXERCISE 17
Extension - The incentre of a triangle
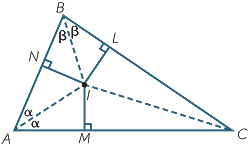
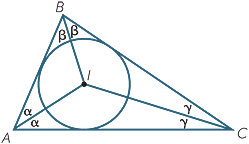 We are now in a position to prove a wonderful theorem
We are now in a position to prove a wonderful theorem
on the angle bisectors of a triangle. These three bisectors are concurrent, and their point of intersection is called the incentre of the triangle. The incentre is the centre of the incircle tangent to all three sides of the triangle, as in the diagram to the right.
Theorem
The angle bisectors of a triangle are concurrent, and the resulting incentre is the centre of the incircle, that is tangent to all three sides.
Proof
We have to prove IC bisects  BCD
BCD
Given  ABC , construct the angle bisectors of
ABC , construct the angle bisectors of  A and
A and  B, and let I be their point of intersection.
B, and let I be their point of intersection.
Join IC, and let α =  BAI =
BAI =  CAI and β =
CAI and β =  ABI =
ABI =  CBI.
CBI.
Drop perpendiculars IL, IM and IN to BC, CA and AB respectively.
EXERCISE 18
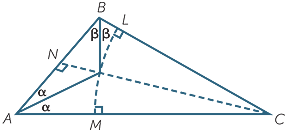 Prove that
Prove that  MAI
MAI 
 NAI and
NAI and NBI
NBI 
 LBI.
LBI. LCI
LCI 
 MCI.
MCI.Summary - The four centres of a triangle
This completes the development of the four best-known centres of a triangle. The results, and the associated terminology and notation, are summarised here for reference.
The left-hand diagram below shows two angles  P and
P and  Q lying in the same segment of a circle − we have proven that these two angles are equal. In the next two diagrams, the angle
Q lying in the same segment of a circle − we have proven that these two angles are equal. In the next two diagrams, the angle  BQU remains equal to
BQU remains equal to  P as the point Q moves around the arc closer and closer to A. In the last diagram, Q coincides with A, and AU is a tangent.
P as the point Q moves around the arc closer and closer to A. In the last diagram, Q coincides with A, and AU is a tangent.
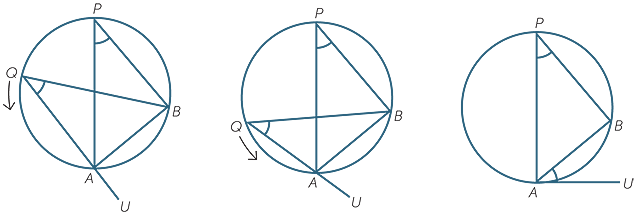
It seems reasonable from these diagrams that in the limiting case, the angle  BAU will still equal
BAU will still equal  P − this is what the alternate segment theorem says.
P − this is what the alternate segment theorem says.
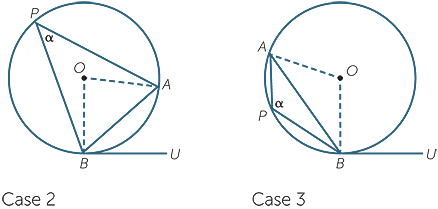
Theorem
An angle between a chord and a tangent is equal to any angle in the alternate segment.
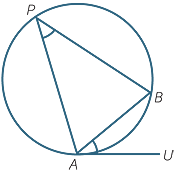 Here
Here  BAU is ‘an angle between a chord and a tangent’.
BAU is ‘an angle between a chord and a tangent’.
The word ‘alternate’ means ‘other’ − the chord AB divides the circle into two segments, and the alternate segment is the segment on the left containing the angle  P. We have already proven that all the angles in this left-hand segment are equal.
P. We have already proven that all the angles in this left-hand segment are equal.
There are two equally satisfactory proofs of this theorem.
One is written out below and the other is left as an exercise.
Proof
Let AB be a chord of a circle and let BU be a tangent at B.
Let P be a point on the arc that is not within the arms of  ABU , and let
ABU , and let  P = α
P = α
There are three cases, depending on whether:
Case 1: The centre O lies on the chord AB.
Case 2: The centre O lies outside the arms of  ABU .
ABU .
Case 3: The centre O lies within the arms of  ABU.
ABU.
In each case, we need to prove that  ABU = α
ABU = α
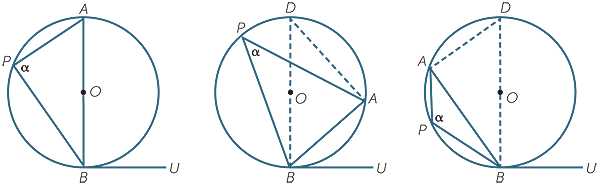
| Case 1 | Case 2 | Case 3 |
Case 1 is easily settled:
α = 90° (angle in a semicircle) ![]() and
and![]()
 ABU = 90° (radius and tangent)
ABU = 90° (radius and tangent)
For the other two cases, construct the diameter BOD, and join DA.
| Case 2: |  ADB ADB |
= α | (angles on the same arc AB) |
|
|
| and |  BAD BAD |
= 90° | (angle in a semicircle) | ||
| so |  DBA DBA |
= 90° − α | (angle sum of  ABD) ABD) |
||
| But |  DBU DBU |
= 90° | (radius and tangent) | ||
| so |  ABU ABU |
= α | (adjacent angles at B) | ||
| Case 3: |  ADB = 180° − α ADB = 180° − α |
(cyclic quadrilateral APBD) |
|
|
| and |  BAD = 90° BAD = 90° |
(angle in a semicircle) | ||
| so |  ABD = α− 90° ABD = α− 90° |
(angle sum of  ABD) ABD) |
||
| But |  DBU = 90° DBU = 90° |
(radius and tangent) | ||
| so |  ABU = α ABU = α |
(adjacent angles at B) | ||
Exercise 19
Find an alternative proof in cases 2 and 3 by constructing the radii AO and BO and using angles at the centre.
The result in the following exercise is surprising. One would not expect parallel lines to emerge so easily in a diagram with two touching circles.
EXERCISE 20
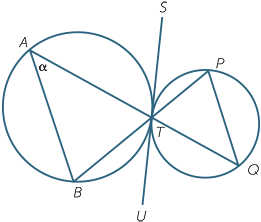 Prove that AB || PQ in the diagram to the right,
Prove that AB || PQ in the diagram to the right,
where STU is a common tangent to both circles.
AQ and BP are straight lines.
The final theorems in this module combine similarity with circle geometry to produce three theorems about intersecting chords, intersecting secants, and the square on a tangent.
Intersecting chords
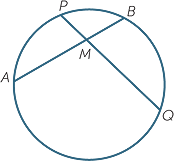 The first theorem deals with chords that intersect within the circle.
The first theorem deals with chords that intersect within the circle.
In this situation, each chord cuts the other into two sub-intervals called intercepts. It is an amazing consequence of similar triangles that, in this situation, the products of the intercepts on each chord are equal. That is, in the diagram to the right, AM × MB = PM × MQ.
Theorem
When two chords intersect within a circle, the products of the intercepts are equal.
Proof
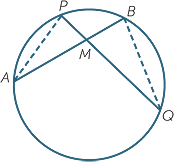 Let AB and PQ be chords intersecting at M. Join AP and BQ.
Let AB and PQ be chords intersecting at M. Join AP and BQ.
In the triangles APM and QBM:
 PAM =
PAM =  BQM (angles on the same arc PB)
BQM (angles on the same arc PB)
 APM =
APM =  QBM (angles on the same arc AQ)
QBM (angles on the same arc AQ)
so  APM is similar to
APM is similar to  QBM (AA):
QBM (AA):
Hence 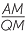 =
= 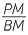 (matching sides of similar triangles)
(matching sides of similar triangles)
so AM × BM = PM × QM.
The very last step is particularly interesting. It converts the equality of two ratios of lengths to the equality of two products of lengths. This is a common procedure when working with similarity.
The sine rule and similarity
Many problems involving similarity can be handled using the sine rule. The exercise below gives an alternative proof of the intersecting chord theorem using the sine rule to deal directly with the ratio of two sides of the triangles.
The remaining two theorems of this section also have alternative proofs using the sine rule.
EXERCISE 21
Use the sine rule in the diagram in the above proof to prove that 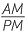 =
=  .
.
Secants from an external point
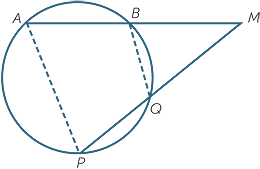 Now suppose that the chords do not meet within
Now suppose that the chords do not meet within
the circle. If they meet on the circle, the identity above holds trivially, and if they are parallel, there is nothing to say. Otherwise, we can produce the chords until they intersect outside the circle, and an analogous theorem applies.
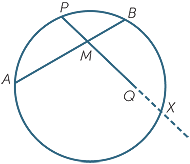
We are now dealing with secants from an external point. When a secant through an external point M meets a circle at two points A and B, the lengths AM and BM are called the intercepts of the secant from the external point, and as before AM × MB = PM × MQ.
Be careful here, the chord AB is not one of the two intercepts. With this definition of intercept, the previous theorem can now be stated as follows. Its proof is word for word almost the same, apart from the reasons:
Theorem
The product of the intercepts on two secants from an external point are equal.
Proof
Let ABM and PQM be two secants from an external point M, as shown.
Join AP and BQ.
EXERCISE 22
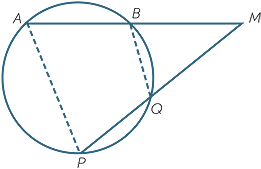 Complete the proof.
Complete the proof.
EXERCISE 23
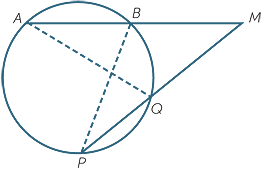 If instead we had joined the intervals AQ and BP, what corresponding changes should be made
If instead we had joined the intervals AQ and BP, what corresponding changes should be made
to the proof?
Tangent and secant from an external point
Now imagine the secant MPQ in the previous diagrams rotating until it becomes a tangent at a point T on the circle. As the secant rotates, the length of each intercept PM and QM gets closer to the length of the tangent TM to the circle from M, so the product PM × QM gets closer to the square TM2 of the tangent from M. This is a proof using limits.
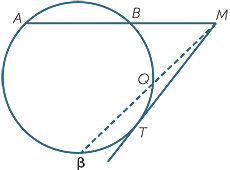 When we draw a secant and a tangent from M, we have seen that the product AM × BM equals the square TM2 of the tangent. The geometric proof is similar to the previous two proofs, but it does require the alternate segment theorem to establish the similarity.
When we draw a secant and a tangent from M, we have seen that the product AM × BM equals the square TM2 of the tangent. The geometric proof is similar to the previous two proofs, but it does require the alternate segment theorem to establish the similarity.
Theorem
The product of the intercepts on a secant from an external point equals the square of the tangent from that point.
Proof
Let ABM be a secant, and TM a tangent, from an external point M, as shown. We need to prove that AM × BM = TM2. Join AT and BT.
EXERCISE 24
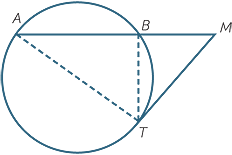 Explain why
Explain why  A =
A =  MTB.
MTB. ATM is similar to
ATM is similar to  TBM.
TBM.The concurrence of three common chords
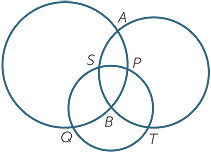 Proving concurrence usually involves logic that is a little
Proving concurrence usually involves logic that is a little
more sophisticated than required in most proofs. The
following theorem is a difficult application of the
intersecting chord theorem.
EXERCISE 25
Show that the three common chords AB, PQ and ST to the three circles in the diagram
above are concurrent.
Circle geometry is often used as part of the solution to problems in trigonometry and calculus.
converse of the circle theorems
The circle theorems proven in this module all have dramatic and important converse theorems, which are tests for points to lie on a circle. The proofs of these converses, and their applications, are usually regarded as inappropriate for Years 9−10, apart from the converse of the angle in a semicircle theorem, which was developed within the module. They are so closely related to the material in this module, however, that they have been fully developed in an Appendix.
Tangents to circles
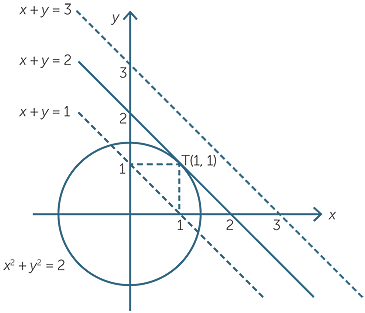 We defined a tangent to a circle as a line with one point in common with the circle. This definition can be used in coordinate geometry using simultaneous equations. For example, the diagram to the right shows the line x + y = 2 and the circle x2 + y2 = 2.
We defined a tangent to a circle as a line with one point in common with the circle. This definition can be used in coordinate geometry using simultaneous equations. For example, the diagram to the right shows the line x + y = 2 and the circle x2 + y2 = 2.
Substituting the equation of the line into the equation of the circle gives
| x2 + (2 − x)2 | = 2 | |
| 2x2 − 4x + 4 | = 2 | |
| x2 − 2x + 1 | = 0 | |
| (x − 1)2 | = 0 |
and the only solution is thus x = 1. Hence the line and the circle have only the single point of intersection T(1, 1), proving that the line is a tangent to the circle.
Similarly, the dotted line x + y = 1 is a secant, intersecting the circle in two points, and the dotted line x + y = 3 does not intersect the circle at all.
Tangents to parabolas
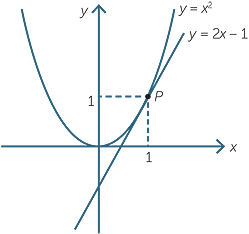 This simultaneous equations approach to tangents can be generalised to other curves defined by algebraic equations.
This simultaneous equations approach to tangents can be generalised to other curves defined by algebraic equations.
For example, the line y = 2x − 1 is a tangent to the graph of the parabola of y = x2 at the point P(1, 1), because solving the equations simultaneously gives
| x2 = 2x − 1 | |
| x2 − 2x + 1 = 0 |
Hence P(1, 1) is the only point of intersection.
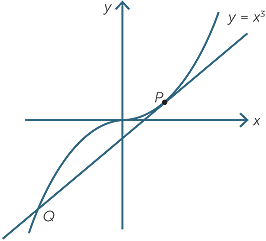 For graphs defined by cubics and higher powers, however, the definition of ‘tangent’ has to be adapted. The first diagram to the right shows that we would think of as a ‘tangent’ at a point P can cross the curve again at some other point, Q.
For graphs defined by cubics and higher powers, however, the definition of ‘tangent’ has to be adapted. The first diagram to the right shows that we would think of as a ‘tangent’ at a point P can cross the curve again at some other point, Q.
The following diagram shows that even with
a quadratic graph, our current definition of ‘tangent’ would mean that every vertical line would be a tangent to the parabola!
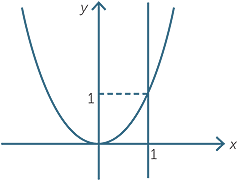 Clearly we need to change the requirement of a single point of intersection, and instead develop some idea about a tangent being a straight line that ‘approximates a curve’ in the neighbourhood of the point of contact.
Clearly we need to change the requirement of a single point of intersection, and instead develop some idea about a tangent being a straight line that ‘approximates a curve’ in the neighbourhood of the point of contact.
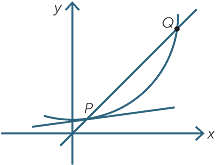 These considerations lead naturally to the well-known limiting process. To construct a tangent at a point P on a general curve, we construct the secant through P and another point Q on the curve, and then move the point Q closer and closer to P. This is the traditional beginning of calculus at school.
These considerations lead naturally to the well-known limiting process. To construct a tangent at a point P on a general curve, we construct the secant through P and another point Q on the curve, and then move the point Q closer and closer to P. This is the traditional beginning of calculus at school.
Applications in motion and rates of change
When a stone on a string is whirled around in a circle, then suddenly let go, it flies off at a tangent to the circle (ignoring the subsequent fall to the ground). We can interpret this situation by saying that the tangent describes the direction in which the stone was travelling at the instant when it was released. This leads to the concept of a vector which has both magnitude and direction representing the velocity particle.
The study of motion begins with motion in a straight line, that is, in one dimension. When motion in two dimensions is first considered, circular paths and parabolic paths are the first paths to be considered, because they are reasonably straightforward to describe mathematically, and they arise in so many practical situations.
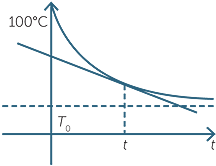 A rate of change is also described by a tangent. This time the tangent does not have any physical significance, but it is the gradient of the tangent that gives the instantaneous rate of change. For example, when boiling water is removed from the stove and cools, the temperature−time graph looks something like the graph to the right. At any time t, the rate at which the water is cooling is given by the gradient of the tangent at the corresponding point on the curve.
A rate of change is also described by a tangent. This time the tangent does not have any physical significance, but it is the gradient of the tangent that gives the instantaneous rate of change. For example, when boiling water is removed from the stove and cools, the temperature−time graph looks something like the graph to the right. At any time t, the rate at which the water is cooling is given by the gradient of the tangent at the corresponding point on the curve.
Vectors and complex numbers
Problems in complex numbers often require locating a set of complex numbers on the complex plane. The following example requires some knowledge of vectors and circle geometry.
EXAMPLE
Sketch the set of complex numbers such that the ratio 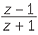 is an imaginary number, that is a real multiple of i.
is an imaginary number, that is a real multiple of i.
Solution
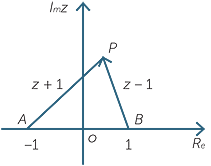 If
If![]() z = 1, then
z = 1, then 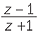 = 0, which is imaginary.
= 0, which is imaginary.
If![]() z = −1, then
z = −1, then 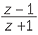 is not defined.
is not defined.
So suppose that z is neither 1 nor −1.
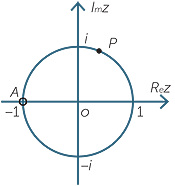 The condition on z is that z − 1 is ki times z + 1, where k is real. We know that multiplying by ki rotates the direction of a complex number by 90° or by −90°. That is, the vector z − 1 is perpendicular to the vector z + 1. We know that z − 1 is a vector with tail at 1 and head at z, and that z + 1 is a vector with tail at −1 and head at z. Let A, B and P represent the points −1, 1 and z. Then the condition becomes
The condition on z is that z − 1 is ki times z + 1, where k is real. We know that multiplying by ki rotates the direction of a complex number by 90° or by −90°. That is, the vector z − 1 is perpendicular to the vector z + 1. We know that z − 1 is a vector with tail at 1 and head at z, and that z + 1 is a vector with tail at −1 and head at z. Let A, B and P represent the points −1, 1 and z. Then the condition becomes  APB is a right angle. Thus the locus of z is a circle with diameter AB, that is a circle of radius 1 and centre 0, excluding −1.
APB is a right angle. Thus the locus of z is a circle with diameter AB, that is a circle of radius 1 and centre 0, excluding −1.
Many problems similar to this involve not just the theorems developed in the module, but their converses as well, as developed in the Appendix to this module.
Greek geometry was based on the constructions of straight lines and circles, using a straight edge and compasses, which naturally gave circles a central place in their geometry. All the theorems developed in the Content and Appendix of this module
were developed by the Greeks, and appear in Euclid’s Elements.
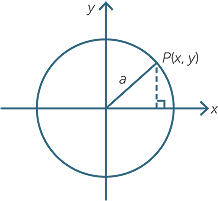 In coordinate geometry, developed later by Descartes in the 17th century, horizontal and vertical lengths are measured against the two axes, and diagonal lengths are related to them using Pythagoras’ theorem. The resulting connection between circles and Pythagoras’ theorem is seen in the equation of a circle.
In coordinate geometry, developed later by Descartes in the 17th century, horizontal and vertical lengths are measured against the two axes, and diagonal lengths are related to them using Pythagoras’ theorem. The resulting connection between circles and Pythagoras’ theorem is seen in the equation of a circle.
The square of the distance of a point P(x, y) from the origin is x2 + y2 by Pythagoras’ theorem, which means that the equation of the circle with radius a and centre the origin is x2 + y2 = a2.
A circle is a simple closed curve with an inside and an outside, a property that it shares with triangles and quadrilaterals. In three dimensions, spheres, cubes and toruses (doughnuts) have an inside and an outside, but a torus is clearly connected in a different way from a sphere. The subject called topology, begun by Euler and developed extensively in the 20th century, begins with such observations.
Greek astronomy made great use of circles and spheres. They knew that the Earth was round, and were able to calculate its circumference with reasonable accuracy. Ptolemy described the heavenly bodies in terms of concentric spheres on which the Moon, the planets, the Sun and the stars were embedded. When astronomy was reconstructed in the 16th century by Copernicus, the heavenly spheres disappeared, but he still used circles for orbits, with the centre moved from the Earth to the Sun. Ellipses and other refinements of the orbits were soon introduced into this basic model of circles by Kepler, who empirically found three laws of motion for planets. At the end of the 17th century Newton used calculus, his laws of motion and the universal law of gravitation to derive Kepler’s laws.
John Dalton reconstructed chemistry at the start of the 19th century on the basis of atoms, which he regarded as tiny spheres, and in the 20th century, models of circular orbits and spherical shells were originally used to describe the motion of electrons around the spherical nucleus. Thus circles and their geometry have always remained at the heart of theories about the microscopic world of atoms and theories about the cosmos and the universe.
Geometry continues to play a central role in modern mathematics, but its concepts, including many generalisations of circles, have become increasingly abstract. For example, spheres in higher dimensional space came to notice in 1965, when John Leech and John Conway made a spectacular contribution to modern algebra by studying an extremely close packing of spheres in 24-dimensional space.
On the other hand, classical Euclidean geometry in the form presented in this module has nevertheless advanced in modern times − here are three results obtained in recent centuries.
In 1765, Euler discovered that:
The orthocentre, the circumcentre, and the centroid of any triangle are collinear.
The centroid divides the interval joining the circumcentre and the orthocentre in
the ratio 2:1.
The line joining these three centres is now called the Euler line. The proof is reasonably straightforward, and is presented in the following exercise.
EXERCISE 26
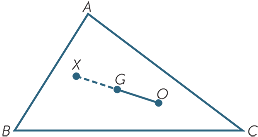 In the diagram to the right, G and O are respectively the centroid and the circumcentre of
In the diagram to the right, G and O are respectively the centroid and the circumcentre of  ABC. The interval OG is produced to X so that OG : GX = 1 : 2. We shall prove that X is the orthocentre of
ABC. The interval OG is produced to X so that OG : GX = 1 : 2. We shall prove that X is the orthocentre of  ABC by proving that it lies on each of the three altitudes of the triangle. Join AX. Let M be the midpoint of BC. Join the median AGM, and the perpendicular OM.
ABC by proving that it lies on each of the three altitudes of the triangle. Join AX. Let M be the midpoint of BC. Join the median AGM, and the perpendicular OM.
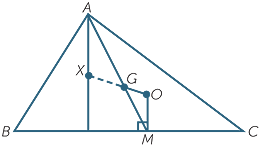 Prove that
Prove that  AGX is similar to
AGX is similar to  MGO, with similarity ratio 2:1.
MGO, with similarity ratio 2:1. ABC.
ABC.In the early 19th century, Poncelet, Feuerbach and others showed that in any triangle,
the following nine points are cyclic:
That is, these nine points lie on a circle.
He also showed that the centre of this nine-point circle lies on the Euler line, and is the midpoint of the interval joining the circumcentre to the orthocentre.
Again, the proof is straightforward enough to present here as a structured exercise, although proving that the centre of the nine-point circle is the midpoint of OH is rather fiddly.
EXERCISE 27
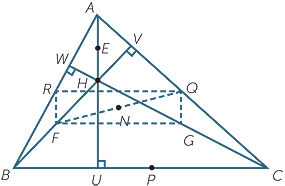 The diagram to the right shows
The diagram to the right shows  ABC with the altitudes AU, BV and CW meeting at the orthocenter H. The points E, F and G are the respective midpoints of AH, BH and CH. The points P, Q and R are the midpoints of the sides BC, CA and AB.
ABC with the altitudes AU, BV and CW meeting at the orthocenter H. The points E, F and G are the respective midpoints of AH, BH and CH. The points P, Q and R are the midpoints of the sides BC, CA and AB.
 FQV, prove that N is equidistant from Q and V, and hence that the circle also passes through U, V and W.
FQV, prove that N is equidistant from Q and V, and hence that the circle also passes through U, V and W.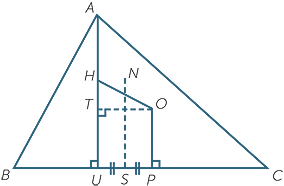 The diagram to the right shows the altitude AU, the midpoint P of BC, the midpoint S of UP, and the circumcentre O, orthocentre H, and nine-point centre N.
The diagram to the right shows the altitude AU, the midpoint P of BC, the midpoint S of UP, and the circumcentre O, orthocentre H, and nine-point centre N.An enlargement transformation associated with Euler’s line and the nine-point circle
Here is a rather dramatic proof using a single enlargement that establishes the existence of the Euler line and the positions on it of the centroid G, the circumcentre O, the orthocentre H, and the nine-point centre N. The notation is the same as that used in exercises 25 and 26.
In this construction, all that is used about the nine-point circle point is that it is the circle through P, Q and R. The fact that the other six points lie on it would be proven afterwards.
The medians trisect each other, so
![]() AG : GP = BG : GQ = CG : GR = 2 : 1.
AG : GP = BG : GQ = CG : GR = 2 : 1.
Consider the enlargement with centre G and enlargement factor − .
.
This enlargement fixes G, and maps A to P, B to Q and C to R, so the circumcircle of  ABC is mapped to the circumcircle of
ABC is mapped to the circumcircle of  PQR. Thus the circumcentre O is mapped to the nine-point centre N, and G thus divides NO in the ratio 1 : 2. The orthocentre H of
PQR. Thus the circumcentre O is mapped to the nine-point centre N, and G thus divides NO in the ratio 1 : 2. The orthocentre H of  ABC is mapped to the orthocentre of
ABC is mapped to the orthocentre of  PQR, and the orthocentre of
PQR, and the orthocentre of  PQR is the circumcentre O of
PQR is the circumcentre O of  ABC, because the perpendicular bisectors of the sides of
ABC, because the perpendicular bisectors of the sides of  ABC are the altitudes of
ABC are the altitudes of  PQR, so G divides HO in the ratio 2 : 1. Thus the four points H, N, G and O are collinear, with
PQR, so G divides HO in the ratio 2 : 1. Thus the four points H, N, G and O are collinear, with
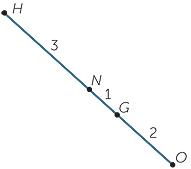
![]() HN : NG : GO = 3 : 1 : 2.
HN : NG : GO = 3 : 1 : 2.
It also follows that the nine-point circle has half the radius of the circumcircle.
 In 1899, the American mathematician Frank Morley discovered an amazing equilateral triangle that is formed inside every triangle. When each angle of a triangle is trisected, the points of intersection of trisectors of adjacent vertices form an equilateral triangle.
In 1899, the American mathematician Frank Morley discovered an amazing equilateral triangle that is formed inside every triangle. When each angle of a triangle is trisected, the points of intersection of trisectors of adjacent vertices form an equilateral triangle.
The result has many proofs by similar triangles, and we refer the reader particularly to John Conway’s proof and Bollobas’ version.
The result can also be proven using the compound angle formulae of trigonometry, and is thus reasonably accessible to students in senior calculus courses. See
https://en.wikipedia.org/wiki/Morley%27s_triangle
https://www.cut-the-knot.org/triangle/Morley/
Appendix − Converses to the Circle Theorems
These proofs are best written as proofs by contradiction. The original theorem is used in the proof of each converse theorem. We have seen this approach when Pythagoras’ theorem was used to prove the converse of Pythagoras’ theorem.
The converse of the angle at the centre theorem
The key theorem of the present module is, ‘An angle at the circumference of a circle is half the angle at the centre subtended by the same arc.’ The most straightforward converse of this is:
Theorem
Let  OAB be isosceles with OA = OB, and let P be a point on the same side of the interval AB as O. Suppose that AB subtends an angle at P half the size of the angle
OAB be isosceles with OA = OB, and let P be a point on the same side of the interval AB as O. Suppose that AB subtends an angle at P half the size of the angle  AOB. Then the circle with centre O through A and B passes through P .
AOB. Then the circle with centre O through A and B passes through P .
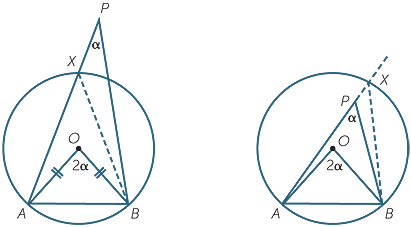
Proof
Let  APB = a and
APB = a and  AOB = 2a. Construct the circle through A and B. Suppose, by way of contradiction, that the circle does not pass through P, and let the circle cross AP, produced if necessary, at X. Join BX.
AOB = 2a. Construct the circle through A and B. Suppose, by way of contradiction, that the circle does not pass through P, and let the circle cross AP, produced if necessary, at X. Join BX.
| Then |  AXB AXB |
=   AOB AOB |
(angles at centre and circumference on the same arc AB) | ||
| = α | |||||
| so | BX || BP | (corresponding angles are equal); | |||
so the lines BX and PX coincide, and hence the points X and P coincide. Thus P lies on the circle, contradicting the assumption that the circle does not pass through P.
Testing whether four given points are concyclic
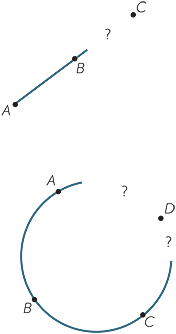 One of the basic axioms of geometry is that a line
One of the basic axioms of geometry is that a line
can be drawn through any two distinct points A and B. When there are three distinct points A, B and C, we can ask whether the three points are collinear, or form a triangle.
Similarly, any three non-collinear points A, B and C are concyclic. When there are four points A, B, C and D, no three collinear, we can ask whether these four points are concyclic, that is, do they lie on a circle.
The remaining converse theorems all provide tests as to whether four given points are concyclic. In each case, we draw the unique circle through three of them and prove that the fourth point lies on this circle.
We shall assume that the fourth point does not lie on the circle and produce a contradiction.
The converse of the angles on the same arc theorem
Theorem
If an interval subtends equal angles at two points on the same side of the interval, then the two points and the endpoints of the interval are concyclic.
Proof
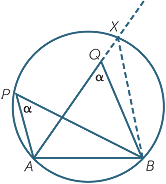 Let the interval AB subtend equal angles a at points P and Q on the same side of BC. Construct the circle through A, B and P, and suppose, by way of contradiction, that the circle does not pass through Q.
Let the interval AB subtend equal angles a at points P and Q on the same side of BC. Construct the circle through A, B and P, and suppose, by way of contradiction, that the circle does not pass through Q.
Let AQ, produced if necessary, meet the circle again at X.
| Then |  AXB = α AXB = α |
(angles on the same arc AB), | ||
| so | BX || BQ | (corresponding angles are equal) | ||
| Hence BQ and BX are the same line, so Q coincides with X, which is a contradiction. | ||||
A test for a cyclic quadrilateral
We proved earlier, as extension content, two tests for a cyclic quadrilateral:
The proof by contradiction of the first test is almost identical to the proof of the previous converse theorem. The second test is a simple corollary of the first test.
The intersecting chord test
We proved that the product of the intercepts of intersecting chords are equal. The converse of this gives yet another test for four points to be concyclic. The proof proceeds along exactly the same lines.
Theorem
Let AB and PQ be intervals intersecting at M, with AM × BM = PM × QM. Then the four endpoints A, B, P and Q are concyclic.
EXERCISE 28
Complete the proof of this theorem.
We leave it the reader to formulate and prove the (true) converses to the remaining two theorems about secants from an external point, and a tangent and a secant from an external point. By similar methods, one can also prove the converse of the theorem
that if a quadrilateral has an incircle, then the sums of its opposite sides are equal.
EXERCISE 1
 ‘maps’
‘maps’  onto itself.
onto itself. . Then reflection in the line m through O perpendicular to
. Then reflection in the line m through O perpendicular to  ,
, onto itself (and are identical in their action
onto itself (and are identical in their action ).
). fixes the line
fixes the line  , because it fixes every point on
, because it fixes every point on  .
. onto itself, and maps P to Q.
onto itself, and maps P to Q. onto itself, and exchanges the points P and Q. (Rotation of 180° about the midpoint of PQ does
onto itself, and exchanges the points P and Q. (Rotation of 180° about the midpoint of PQ doesEXERCISE 2
Use simple trigonometry in  AMO.
AMO.
EXERCISE 3
All radii of a circle are equal, so OA = OB = OP = OQ, so the quadrilateral APBQ is a rectangle because its diagonals are equal and bisect each other. Hence  APB is a right angle.
APB is a right angle.
EXERCISE 4
 At all times, the front of the building is the hypotenuse of aright-angled triangle whose third vertex is the photographer. Hence the circle with diameter, the front of the building, always pass through the photographer, and his possible positions are the points on the semicircle in front of the building.
At all times, the front of the building is the hypotenuse of aright-angled triangle whose third vertex is the photographer. Hence the circle with diameter, the front of the building, always pass through the photographer, and his possible positions are the points on the semicircle in front of the building.
EXERCISE 5
At all times, the triangle formed by the plank, the wall and the floor is right-angled with hypotenuse of length  metres. By the converse theorem above, the midpoint of the plank is therefore always
metres. By the converse theorem above, the midpoint of the plank is therefore always 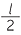 metres from the corner. Hence the midpoint traces out a quadrant of the circle with centre at the corner and radius
metres from the corner. Hence the midpoint traces out a quadrant of the circle with centre at the corner and radius 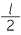 metres.
metres.
EXERCISE 6
Case 2: It will be sufficient to prove the result when O lies on AP.
| Let |  OBP OBP |
= β. | |||
| Then |  BPO BPO |
= β | (base angles of isosceles  OBP), OBP), |
||
| so |  AOB AOB |
= 2β = 2 ×  APB APB |
(exterior angle of  OBP). OBP). |
Case 3: Join PO and produce PO to Q.
| Let |  OAP OAP |
= α | |||
| and |  OBP OBP |
= β | (base angles of isosceles  OBP), OBP), |
||
| Then |  APO APO |
= α | (base angle of issosceles  AOP) AOP) |
||
 OPB OPB |
= β | (base angle of  OBP) OBP) |
|||
| Hence |  APB APB |
= β − α | |||
| Also |  AOQ AOQ |
= 2α | (exterior angle of  OAP) OAP) |
||
| and |  BOQ BOQ |
= 2β | (exterior angle of  OBP) OBP) |
||
| Hence |  AOB AOB |
= 2β − 2α = 2(β − α) = 2 ×  APB APB |
|||
EXERCISE 7
 ABQ =
ABQ =  RCA by parts c and d, and
RCA by parts c and d, and  A is common, so
A is common, so  ARC =
ARC =  AQB = 90°.
AQB = 90°.EXERCISE 8
 DAC and
DAC and  DBC stand on the same arc DC, so
DBC stand on the same arc DC, so  DBC = α.
DBC = α. BDC = β
BDC = β  ABD = γ
ABD = γ  ADB = δ
ADB = δ EXERCISE 9
Join the common chord BQ, and produce ABC to X, and let a =  A.
A.
| Then |  BQR = α BQR = α |
(opposite exterior angle of cyclic quadrilateral) | ||
| and |  RCX = α RCX = α |
(opposite exterior angle of cyclic quadrilateral), | ||
| so | AP || CR | (corresponding angles are equal) | ||
EXERCISE 10
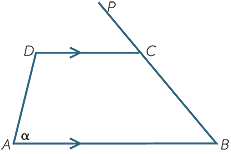 In this proof, we construct two isosceles triangles.
In this proof, we construct two isosceles triangles.
Let ABCD be a cyclic trapezium with AB || DC. Since ABCD is not a rectangle, and its angles add to 360°, one of its angles is acute.
| Let |  A = α be acute, and produce BC to P. A = α be acute, and produce BC to P. |
|||
| Then |  DCP = α DCP = α |
(opposite exterior angle of cyclic quadrilateral) | ||
| so |  B = α B = α |
(corresponding angles, AB || DC). | ||
| Hence |  B is also acute, so AD and BC produced meet at a point M, B is also acute, so AD and BC produced meet at a point M, |
|||
| and |  CDM = α CDM = α |
(corresponding angles, AB || DC). | ||
Hence  DMC and
DMC and  AMB are both isosceles, with DM = CM and AM = BM , so AD = BC.
AMB are both isosceles, with DM = CM and AM = BM , so AD = BC.
EXERCISE 11
The adjacent interior angle is supplementary to the exterior angle, and therefore equal to the opposite interior angle. Hence the quadrilateral is cyclic by the theorem.
EXERCISE 12
 D = D = |
180° − α | (co-interior angles, AB || DC ) | |||
| so |  D + D +  B = B = |
180° |
Hence the quadrilateral ABCD is cyclic (opposite angles are supplementary).
EXERCISE 13
| a | In Case 1, |  BCP BCP |
= 90° | (angle in a semicircle) | |||
| and |  P P |
= α | (angles on the same arc BC) | ||||
| Hence | 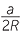 |
= sin α | (simple trigonometry in  BCP) BCP) |
||||
| so |  |
= 2R. | |||||
| b | In Case 2, |  BCP BCP |
= 90° | (angle in a semicircle) | |||
| and |  P P |
= 180° − α | (opposite angles of cyclic quadrilateral BACP) | ||||
| so | sin P | = sin (180° − α ) = sin α | |||||
| Hence | 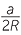 |
= sin α | (simple trigonometry in  BCP) BCP) |
||||
 |
= 2R. | ||||||
| c | In Case 3, | α | = 90° | (angle in a semicircle), | |||
| so | sin α | = 1. | |||||
| The diameter of the circumcircle is a, | |||||||
| so |  |
= 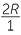 = 2R. = 2R. |
|||||
EXERCISE 14
Let tangents from an external point P touch the circle at T and U.
Join the radii OT and OU and the interval OP.
Since OP is common, the radii are equal, and the radii are perpendicular to the tangents,
 OPT OPT |
  OPU OPU |
(RHS) | |||
| so | PT | = PU | (matching sides of congruent triangles). |
EXERCISE 15
The triangle OPT is right-angled at T. The rest is simple trigonometry.
EXERCISE 16
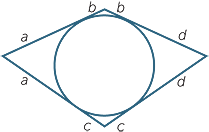 Tangents from an external point are equal, so we can label the lengths in the figure as shown. Then both sums of opposite sides of the quadrilateral are a + b + c + d.
Tangents from an external point are equal, so we can label the lengths in the figure as shown. Then both sums of opposite sides of the quadrilateral are a + b + c + d.
EXERCISE 17
EXERCISE 18
 Use the AAS test.
Use the AAS test. LCI =
LCI =  MCI, so IC is also an angle bisector, thus proving the concurrence of the angle bisectors. Also the circle with centre I and radius LI = MI = NI is tangent to all three sides by the radius-and-tangent theorem.
MCI, so IC is also an angle bisector, thus proving the concurrence of the angle bisectors. Also the circle with centre I and radius LI = MI = NI is tangent to all three sides by the radius-and-tangent theorem.EXERCISE 19
| In Case 2, |  AOB AOB |
= | 2α | (angles at centre and circumference on same arc AB) | |
| so |  OBA OBA |
= | 90° −α | (angle sum of isosceles  OAB) OAB) |
|
| But |  OBU OBU |
= | 90° | (radius and tangent) | |
| so |  ABU ABU |
= | α | (adjacent angles at B). | |
| In Case 3, | reflex  AOB AOB |
= | 2α | (angles at centre and circumference on same arc AB) | |
| so | non-reflex  AOB AOB |
= | 360° − 2α | (angles in a revolution) | |
 OBA OBA |
= | α − 90° | (angle sum of isosceles  OAB) OAB) |
||
 OBU OBU |
= | 90° | (radius and tangent) | ||
 ABU ABU |
= | α | (adjacent angles at B). | ||
EXERCISE 20
| Let | α | =  A. A. |
||
| Then |  BTU BTU |
= α | (alternate segment theorem) | |
| so |  STP STP |
= α | (vertically opposite angles) | |
| so |  Q Q |
= α | (alternate segment theorem) | |
| Hence AB || PQ | (alternate angles are equal). | |||
EXERCISE 21
We have already proven that  A =
A =  Q and that
Q and that  P =
P =  B.
B.
The sine rule 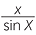 =
=  in a triangle XYZ can also be written in the form
in a triangle XYZ can also be written in the form
![]()
 =
= 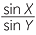
Using this form of the sine rule in the two triangles,
![]()
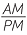 =
= 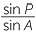 =
= 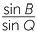 =
= 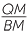 .
.
EXERCISE 22
Proof: In the triangles APM and QBM :
 PAM = PAM =  BQM BQM |
(exterior angle of cyclic quadrilateral ABQP) | ||||
 AMP = AMP =  BMQ BMQ |
(common angle) | ||||
| so |  APM is similar to APM is similar to  QBM (AA). QBM (AA). |
||||
| Hence | 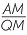 = = 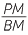 . . |
(matching sides of similar triangles) | |||
| so | AM × BM = PM × QM. |
||||
EXERCISE 23
Proof: In the triangles AQM and PBM :
 A = A =  P P |
(angles on the same arc BQ) | |||
 M is common to both triangles M is common to both triangles |
||||
| so |  AQM is similar to AQM is similar to  PBM PBM |
|||
| Hence | 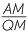 = = 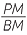 |
(matching sides of similar triangles) | ||
| so | AM × BM = PM × QM | |||
EXERCISE 24
Proof: In the triangles ATM and TBM:
 TAM = TAM =  BTM BTM |
(alternate segment theorem) | |||
 AMT = AMT =  TMB TMB |
(common) | |||
| so |  ATM is similar to ATM is similar to  TBM TBM |
|||
| Hence | 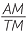 = = 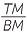 |
(matching sides of similar triangles) | ||
| AM × BM = TM2 | ||||
EXERCISE 25
Let the chords AB and PQ meet at M. Join SM and produce it to meet the circles at X and Y. We need to prove that the points X and Y coincide.
Using the intersecting chord theorem in each circle in turn,
| SM × MX | = AM × MB | (from Circle 1) |
|
||
| = PM × MQ | (from Circle 2) | ||||
| = SM × MY | (from Circle 3). | ||||
EXERCISE 26
 AGX =
AGX =  MGO because they are vertically opposite angles.
MGO because they are vertically opposite angles. AGX is similar to
AGX is similar to  MGO by the SAS similarity test.
MGO by the SAS similarity test. XAG and
XAG and  OMG are equal,
OMG are equal, ABC.
ABC.EXERCISE 27
EXERCISE 28
 Construct the circle through A, B and P, and suppose
Construct the circle through A, B and P, and suppose
by way of contradiction that the circle does not pass through Q.
Let PQ, produced if necessary, meet the circle again at X .
| Then | AM × BM = PM × XM | (intersecting chords) | ||
| so | XM = QM, and Q and X both lie on the same side of M. | |||
Hence X coincides with Q, which is a contradiction.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()
