The Improving Mathematics Education in Schools (TIMES) Project
Parallelograms and Rectangles
Measurement and Geometry : Module 20![]() Years : 8-9
Years : 8-9
June 2011
- Introductory plane geometry involving points and lines, parallel lines and transversals, angle sums of triangles and quadrilaterals, and general angle-chasing.
- The four standard congruence tests and their application in problems and proofs.
- Properties of isosceles and equilateral triangles and tests for them.
- Experience with a logical argument in geometry being written as a sequence of steps, each justified by a reason.
- Ruler-and-compasses constructions.
- Informal experience with special quadrilaterals.
There are only three important categories of special triangles − isosceles triangles, equilateral triangles and right-angled triangles. In contrast, there are many categories of special quadrilaterals. This module will deal with two of them − parallelograms and rectangles − leaving rhombuses, kites, squares, trapezia and cyclic quadrilaterals to the module, Rhombuses, Kites, and Trapezia.
Apart from cyclic quadrilaterals, these special quadrilaterals and their properties have been introduced informally over several years, but without congruence, a rigorous discussion of them was not possible. Each congruence proof uses the diagonals to divide the quadrilateral into triangles, after which we can apply the methods of congruent triangles developed in the module, Congruence.
The present treatment has four purposes:
- The parallelogram and rectangle are carefully defined.
- Their significant properties are proven, mostly using congruence.
- Tests for them are established that can be used to check that a given quadrilateral
is a parallelogram or rectangle − again, congruence is mostly required. - Some ruler-and-compasses constructions of them are developed as simple applications of the definitions and tests.
The material in this module is suitable for Year 8 as further applications of congruence and constructions. Because of its systematic development, it provides an excellent introduction to proof, converse statements, and sequences of theorems. Considerable guidance in such ideas is normally required in Year 8, which is consolidated by further discussion in later years.
The complementary ideas of a ‘property’ of a figure, and a ‘test’ for a figure, become particularly important in this module. Indeed, clarity about these ideas is one of the many reasons for teaching this material at school. Most of the tests that we meet are converses of properties that have already been proven. For example, the fact that the base angles of an isosceles triangle are equal is a property of isosceles triangles. This property can be re-formulated as an ‘If …, then … ’ statement:
- If two sides of a triangle are equal, then the angles opposite those sides are equal.
Now the corresponding test for a triangle to be isosceles is clearly the converse statement:
- If two angles of a triangle are equal, then the sides opposite those angles are equal.
Remember that a statement may be true, but its converse false. It is true that ‘If a number is a multiple of 4, then it is even’, but it is false that ‘If a number is even, then it is a multiple of 4’.
In other modules, we defined a quadrilateral to be a closed plane figure bounded by four intervals, and a convex quadrilateral to be a quadrilateral in which each interior angle is less than 180°. We proved two important theorems about the angles of a quadrilateral:
- The sum of the interior angles of a quadrilateral is 360°.
- The sum of the exterior angles of a convex quadrilateral is 360°.
To prove the first result, we constructed in each case a diagonal that lies completely inside the quadrilateral. This divided the quadrilateral into two triangles, each of whose angle sum is 180°.
To prove the second result, we produced one side at each vertex of the convex quadrilateral. The sum of the four straight angles is 720° and the sum of the four interior angles is 360°, so the sum of the four exterior angles is 360°.
We begin with parallelograms, because we will be using the results about parallelograms when discussing the other figures.
Definition of a parallelogram
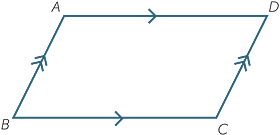 A parallelogram is a quadrilateral whose opposite sides are parallel. Thus the quadrilateral ABCD shown opposite is a parallelogram because AB || DC and DA || CB.
A parallelogram is a quadrilateral whose opposite sides are parallel. Thus the quadrilateral ABCD shown opposite is a parallelogram because AB || DC and DA || CB.
The word ‘parallelogram’ comes from Greek
words meaning ‘parallel lines’.
Constructing a parallelogram using the definition
To construct a parallelogram using the definition, we can use the copy-an-angle construction to form parallel lines. For example, suppose that we are given the intervals AB and AD in the diagram below. We extend AD and AB and copy the angle at A to corresponding angles at B and D to determine C and complete the parallelogram ABCD. (See the module, Construction.)
This is not the easiest way to construct a parallelogram.
First property of a parallelogram − The opposite angles are equal
The three properties of a parallelogram developed below concern first, the interior angles, secondly, the sides, and thirdly the diagonals. The first property is most easily proven using angle-chasing, but it can also be proven using congruence.
Theorem
 The opposite angles of a parallelogram are equal.
The opposite angles of a parallelogram are equal.
Proof
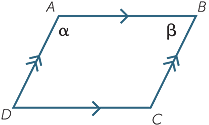
Let ABCD be a parallelogram, with  A = α and A = α and  B = β. B = β. |
||||||
Prove that  C = α and C = α and  D = β. D = β. |
||||||
| α + β | = 180° | (co-interior angles, AD || BC), | ||||
| so |
 C C
|
= α | (co-interior angles, AB || DC) | |||
| and |
 D D
|
= β | (co-interior angles, AB || DC). | |||
Second property of a parallelogram − The opposite sides are equal
As an example, this proof has been set out in full, with the congruence test fully developed. Most of the remaining proofs however, are presented as exercises, with an abbreviated version given as an answer.
Theorem
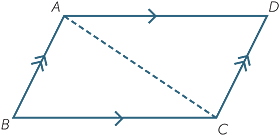 The opposite sides of a parallelogram are equal.
The opposite sides of a parallelogram are equal.
Proof
| ABCD is a parallelogram. | ||||
| To prove that AB = CD and AD = BC. | ||||
| Join the diagonal AC. | ||||
| In the triangles ABC and CDA: | ||||
 BAC BAC |
=  DCA DCA |
(alternate angles, AB || DC) |
||
 BCA BCA |
=  DAC DAC |
(alternate angles, AD || BC) | ||
| AC | = CA | (common) | ||
so ABC ≡ ABC ≡  CDA (AAS) CDA (AAS) |
||||
| Hence AB = CD and BC = AD |
||||
![]()
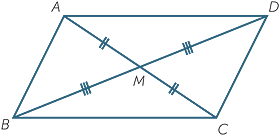
Third property of a parallelogram − The diagonals bisect each other
Theorem
The diagonals of a parallelogram bisect each other.
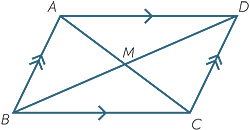 EXERCISE 1
EXERCISE 1
a![]() Prove that
Prove that  ABM ≡
ABM ≡  CDM.
CDM.
b![]() Hence prove that the diagonals bisect each other.
Hence prove that the diagonals bisect each other.
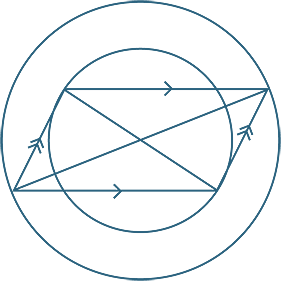 As a consequence of this property, the intersection of the diagonals is the centre of two concentric circles, one through each pair of opposite vertices.
As a consequence of this property, the intersection of the diagonals is the centre of two concentric circles, one through each pair of opposite vertices.
Notice that, in general, a parallelogram does not have a circumcircle through all four vertices.
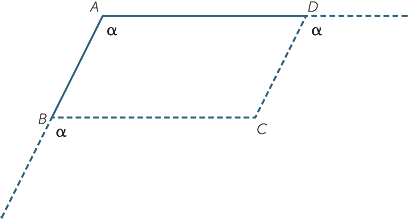
First test for a parallelogram − The opposite angles are equal
Besides the definition itself, there are four useful tests for a parallelogram. Our first test is the converse of our first property, that the opposite angles of a quadrilateral are equal.
Theorem
If the opposite angles of a quadrilateral are equal, then the quadrilateral is a parallelogram.
EXERCISE 2
Prove this result using the figure below.

Second test for a parallelogram − Opposite sides are equal
This test is the converse of the property that the opposite sides of a parallelogram are equal.
Theorem
If the opposite sides of a (convex) quadrilateral are equal, then the quadrilateral is a parallelogram.
EXERCISE 3
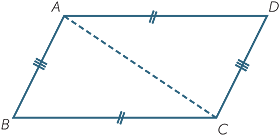 Prove this result using congruence in the figure to the right, where the diagonal AC has been joined.
Prove this result using congruence in the figure to the right, where the diagonal AC has been joined.
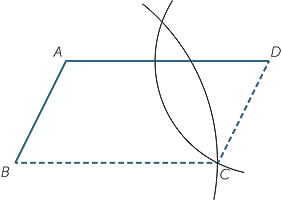 This test gives a simple construction of a parallelogram given two adjacent sides − AB and AD in the figure to the right. Draw a circle with centre B and radius AD, and another circle with centre D and radius AB. The circles intersect at two points − let C be the point of intersection within the non-reflex angle
This test gives a simple construction of a parallelogram given two adjacent sides − AB and AD in the figure to the right. Draw a circle with centre B and radius AD, and another circle with centre D and radius AB. The circles intersect at two points − let C be the point of intersection within the non-reflex angle  BAD. Then ABCD is a parallelogram because its opposite sides are equal.
BAD. Then ABCD is a parallelogram because its opposite sides are equal.
 It also gives a method of drawing the line parallel to a given line through a given point P.
It also gives a method of drawing the line parallel to a given line through a given point P.
Choose any two points A and B on  , and complete the parallelogram PABQ.
, and complete the parallelogram PABQ.
Then PQ || 
Third test for a parallelogram − One pair of opposite sides are equal and parallel
This test turns out to be very useful, because it uses only one pair of opposite sides.
Theorem
If one pair of opposite sides of a quadrilateral are equal and parallel, then the quadrilateral is a parallelogram.
 EXERCISE 4
EXERCISE 4
Complete the proof using the figure on the right.
This test for a parallelogram gives a quick and easy way to construct a parallelogram using a two-sided ruler. Draw a 6 cm interval on each side of the ruler. Joining up the endpoints gives a parallelogram.

 The test is particularly important in the later theory of vectors. Suppose that
The test is particularly important in the later theory of vectors. Suppose that ![]() and
and ![]() are two directed intervals that are parallel and have the same length − that is, they represent the same vector. Then the figure ABQP to the right is a parallelogram.
are two directed intervals that are parallel and have the same length − that is, they represent the same vector. Then the figure ABQP to the right is a parallelogram.
Even a simple vector property like the commutativity of the addition of vectors depends on this construction. The parallelogram ABQP shows, for example, that
![]()
![]() +
+ ![]() =
= ![]() =
= ![]() +
+ ![]()
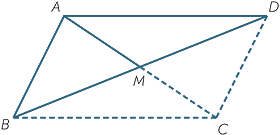
Fourth test for a parallelogram − The diagonals bisect each other
This test is the converse of the property that the diagonals of a parallelogram bisect
each other.
Theorem
If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram:
EXERCISE 5
Complete the proof using the diagram below.
 This test gives a very simple construction of a parallelogram. Draw two intersecting lines, then draw two circles with different radii centred on their intersection. Join the points where alternate circles cut the lines. This is a parallelogram because the diagonals bisect each other.
This test gives a very simple construction of a parallelogram. Draw two intersecting lines, then draw two circles with different radii centred on their intersection. Join the points where alternate circles cut the lines. This is a parallelogram because the diagonals bisect each other.
It also allows yet another method of completing an angle  BAD to a parallelogram, as shown in the following exercise.
BAD to a parallelogram, as shown in the following exercise.
EXERCISE 6
 Given two intervals AB and AD meeting at a common vertex A, construct the midpoint M of BD. Complete this to a construction of the parallelogram ABCD, justifying your answer.
Given two intervals AB and AD meeting at a common vertex A, construct the midpoint M of BD. Complete this to a construction of the parallelogram ABCD, justifying your answer.
Parallelograms
Definition of a parallelogram
A parallelogram is a quadrilateral whose opposite sides are parallel.
Properties of a parallelogram
- The opposite angles of a parallelogram are equal.
- The opposite sides of a parallelogram are equal.
- The diagonals of a parallelogram bisect each other.
Tests for a parallelogram
A quadrilateral is a parallelogram if:
- its opposite angles are equal, or
- its opposite sides are equal, or
- one pair of opposite sides are equal and parallel, or
- its diagonals bisect each other.
The word ‘rectangle’ means ‘right angle’, and this is reflected in its definition.
 Definition of a Rectangle
Definition of a Rectangle
A rectangle is a quadrilateral in which
all angles are right angles.
First Property of a rectangle − A rectangle is a parallelogram
Each pair of co-interior angles are supplementary, because two right angles add to a straight angle, so the opposite sides of a rectangle are parallel. This means that a rectangle is a parallelogram, so:
- Its opposite sides are equal and parallel.
- Its diagonals bisect each other.
Second property of a rectangle − The diagonals are equal
The diagonals of a rectangle have another important property − they are equal in length. The proof has been set out in full as an example, because the overlapping congruent triangles can be confusing.
Theorem
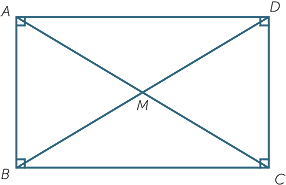 The diagonals of a rectangle are equal.
The diagonals of a rectangle are equal.
Proof
![]() Let ABCD be a rectangle.
Let ABCD be a rectangle.
![]() We prove that AC = BD.
We prove that AC = BD.
![]() In the triangles ABC and DCB:
In the triangles ABC and DCB:
| BC | = CB | (common) | |||||
| AB | = DC | (opposite sides of a parallelogram) | |||||
 ABC ABC |
= DCA = 90° DCA = 90° |
(given) | |||||
![]() so
so![]()
 ABC ≡
ABC ≡  DCB
DCB![]() (SAS)
(SAS)
![]() Hence AC = DB (matching sides of congruent triangles).
Hence AC = DB (matching sides of congruent triangles).
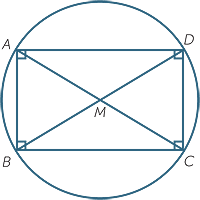 This means that AM = BM = CM = DM, where M is the
This means that AM = BM = CM = DM, where M is the
intersection of the diagonals. Thus we can draw a single
circle with centre M through all four vertices. We can
describe this situation by saying that, ‘The vertices of
a rectangle are concyclic’.
EXERCISE 7
Give an alternative proof of this result using Pythagoras’ theorem.
First test for a rectangle − A parallelogram with one right angle
If a parallelogram is known to have one right angle, then repeated use of co-interior angles proves that all its angles are right angles.
Theorem
If one angle of a parallelogram is a right angle, then it is a rectangle.
Because of this theorem, the definition of a rectangle is sometimes taken to be ‘a parallelogram with a right angle’.
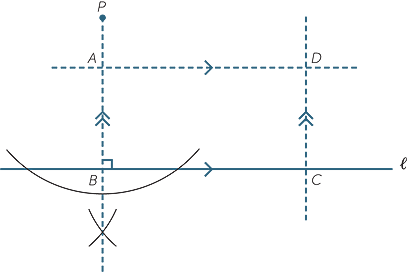
Construction of a rectangle
We can construct a rectangle with given side lengths by constructing a parallelogram with a right angle on one corner. First drop a perpendicular from a point P to a line  . Mark B and then mark off BC and BA and complete the parallelogram as shown below.
. Mark B and then mark off BC and BA and complete the parallelogram as shown below.
Second test for a rectangle − A quadrilateral with equal diagonals that bisect
each other
We have shown above that the diagonals of a rectangle are equal and bisect each other. Conversely, these two properties taken together constitute a test for a quadrilateral to be a rectangle.
Theorem
A quadrilateral whose diagonals are equal and bisect each other is a rectangle.
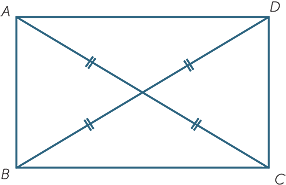 EXERCISE 8
EXERCISE 8
a![]() Why is the quadrilateral a parallelogram?
Why is the quadrilateral a parallelogram?
b![]() Use congruence to prove that the figure is a rectangle.
Use congruence to prove that the figure is a rectangle.
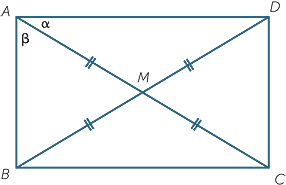 EXERCISE 9
EXERCISE 9
Give an alternative proof of the theorem using angle-chasing.
As a consequence of this result, the endpoints of any two diameters of a circle form a rectangle, because this quadrilateral has equal diagonals that bisect each other.
Thus we can construct a rectangle very simply by drawing any two intersecting lines, then drawing any circle centred at the point of intersection. The quadrilateral formed by joining the four points where the circle cuts the lines is a rectangle because it has equal diagonals that bisect each other.

Rectangles
Definition of a rectangle
A rectangle is a quadrilateral in which all angles are right angles.
Properties of a rectangle
- A rectangle is a parallelogram, so its opposite sides are equal.
- The diagonals of a rectangle are equal and bisect each other.
Tests for a rectangle
- A parallelogram with one right angle is a rectangle.
- A quadrilateral whose diagonals are equal and bisect each other is a rectangle.
The remaining special quadrilaterals to be treated by the congruence and angle-chasing methods of this module are rhombuses, kites, squares and trapezia. The sequence of theorems involved in treating all these special quadrilaterals at once becomes quite complicated, so their discussion will be left until the module Rhombuses, Kites, and Trapezia. Each individual proof, however, is well within Year 8 ability, provided that students have the right experiences. In particular, it would be useful to prove in Year 8 that the diagonals of rhombuses and kites meet at right angles − this result is needed in area formulas, it is useful in applications of Pythagoras’ theorem, and it provides a more systematic explanation of several important constructions.
The next step in the development of geometry is a rigorous treatment of similarity. This will allow various results about ratios of lengths to be established, and also make possible the definition of the trigonometric ratios. Similarity is required for the geometry of circles, where another class of special quadrilaterals arises, namely the cyclic quadrilaterals, whose vertices lie on a circle.
Special quadrilaterals and their properties are needed to establish the standard formulas for areas and volumes of figures. Later, these results will be important in developing integration. Theorems about special quadrilaterals will be widely used in coordinate geometry.
Rectangles are so ubiquitous that they go unnoticed in most applications. One special role worth noting is they are the basis of the coordinates of points in the cartesian plane − to find the coordinates of a point in the plane, we complete the rectangle formed by the point and the two axes. Parallelograms arise when we add vectors by completing the parallelogram − this is the reason why they become so important when complex numbers are represented on the Argand diagram.
Rectangles have been useful for as long as there have been buildings, because vertical pillars and horizontal crossbeams are the most obvious way to construct a building of any size, giving a structure in the shape of a rectangular prism, all of whose faces are rectangles. The diagonals that we constantly use to study rectangles have an analogy in building − a rectangular frame with a diagonal has far more rigidity than a simple rectangular frame, and diagonal struts have always been used by builders to give their building more strength.
Parallelograms are not as common in the physical world (except as shadows of rectangular objects). Their major role historically has been in the representation of physical concepts by vectors. For example, when two forces are combined, a parallelogram can be drawn to help compute the size and direction of the combined force. When there are three forces, we complete the parallelepiped, which is the three-dimensional analogue of the parallelogram.
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
History of Mathematics, D. E. Smith, Dover publications New York, (1958)
EXERCISE 1
a![]() In the triangles ABM and CDM :
In the triangles ABM and CDM :
| 1. |  BAM BAM |
=  DCM DCM |
(alternate angles, AB || DC ) | |||
| 2. |  ABM ABM |
=  CDM CDM |
(alternate angles, AB || DC ) | |||
| 3. | AB | = CD | (opposite sides of parallelogram ABCD) | |||
 ABM = ABM =  CDM CDM |
||||||
b![]() Hence AM = CM and DM = BM
Hence AM = CM and DM = BM![]() (matching sides of congruent triangles)
(matching sides of congruent triangles)
EXERCISE 2
| From the diagram, | 2α + 2β | = 360o | (angle sum of quadrilateral ABCD) | ||
| α + β | = 180o |
| Hence | AB || DC | (co-interior angles are supplementary) | ||
| and | AD || BC | (co-interior angles are supplementary). |
EXERCISE 3
First show that  ABC ≡ ABC ≡  CDA using the SSS congruence test. CDA using the SSS congruence test. |
||||
| Hence |  ACB = ACB =  CAD and CAD and  CAB = CAB =  ACD ACD |
(matching angles of congruent triangles) | ||
| so | AD || BC and AB || DC | (alternate angles are equal.) | ||
EXERCISE 4
First prove that  ABD ≡ ABD ≡  CDB using the SAS congruence test. CDB using the SAS congruence test. |
||||
| Hence |  ADB = ADB =  CBD CBD |
(matching angles of congruent triangles) | ||
| so | AD || BC | (alternate angles are equal.) | ||
EXERCISE 5
First prove that  ABM ≡ ABM ≡  CDM using the SAS congruence test. CDM using the SAS congruence test. |
||||
| Hence | AB = CD | (matching sides of congruent triangles) | ||
| Also |  ABM = ABM =  CDM CDM |
(matching angles of congruent triangles) | ||
| so | AB || DC | (alternate angles are equal): | ||
Hence ABCD is a parallelogram, because one pair of opposite sides are equal and parallel.
EXERCISE 6
Join AM. With centre M, draw an arc with radius AM that meets AM produced at C . Then ABCD is a parallelogram because its diagonals bisect each other.
EXERCISE 7
The square on each diagonal is the sum of the squares on any two adjacent sides. Since opposite sides are equal in length, the squares on both diagonals are the same.
EXERCISE 8![]()
| a |
We have already proven that a quadrilateral whose diagonals bisect each other is a parallelogram. |
| b | Because ABCD is a parallelogram, its opposite sides are equal. | ||||
| Hence |  ABC ≡ ABC ≡  DCB DCB |
(SSS) | |||
| so |  ABC = ABC =  DCB DCB |
(matching angles of congruent triangles). | |||
| But |  ABC + ABC +  DCB = 180o DCB = 180o |
(co-interior angles, AB || DC ) | |||
| so |  ABC = ABC =  DCB = 90o . DCB = 90o . |
||||
![]() Hence ABCD is rectangle, because it is a parallelogram with one right angle.
Hence ABCD is rectangle, because it is a parallelogram with one right angle.
EXERCISE 9
 ADM ADM |
= α | (base angles of isosceles  ADM ) ADM ) |
|||
| and |  ABM ABM |
= β | (base angles of isosceles  ABM ), ABM ), |
||
| so | 2α + 2β | = 180o | (angle sum of  ABD) ABD) |
||
| α + β | = 90o. |
Hence  A is a right angle, and similarly,
A is a right angle, and similarly,  B,
B,  C and
C and  D are right angles.
D are right angles.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


