The Improving Mathematics Education in Schools (TIMES) Project
Trigonometric functions
Measurement and Geometry : Module 25![]() Year : 10
Year : 10
June 2011
- Familiarity with the material in the modules, Introduction to Trigonometry
and Further Trigonometry. - Knowledge of basic coordinate geometry.
- Introductory graphs and functions.
- Facility with simple algebra, formulas and equations.
In the module, Further Trigonometry, we saw how to use points on the unit circle to extend the definition of the trigonometric ratios to include obtuse angles. That same construction can be extended to angles between 180° and 360° and beyond. The sine, cosine and tangent of negative angles can be defined as well.
Once we can find the sine, cosine and tangent of any angle, we can use a table of values to plot the graphs of the functions y = sin x, y = cos x and y = tan x. In this module, we will deal only with the graphs of the first two functions.
The graphs of the sine and cosine functions are used to model wave motion and form the basis for applications ranging from tidal movement to signal processing which is fundamental in modern telecommunications and radio-astronomy. This provides a breathtaking example of how a simple idea involving geometry and ratio was abstracted and developed into a remarkably powerful tool that has changed the world.
Redefining the Trigonometric Ratios
We begin by taking the circle of radius 1, centre the origin, in the plane. From the point P on the circle in the first quadrant we can construct a right-angled triangle POQ with O at the origin and Q on the x-axis.
We mark the angle POQ as θ.
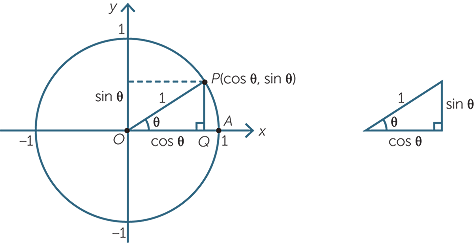
Since the length OQ = cos θ is the x-coordinate of P, and PQ = sin θ is the y-coordinate of P, we see that the point P has coordinates
(cos θ, sin θ).
We measure angles anticlockwise from OA and call these positive angles. Angles measured clockwise from OA are called negative angles. For the time being we will concentrate on positive angles between 0° and 360°.
Since each angle θ determines a point P on the unit circle, we will define
- the cosine of θ to be the x-coordinate of the point P
- the sine of θ to be the y-coordinate of the point P.
For acute angles, we know that tan θ = 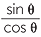 . For angles that are greater than 90° we define the tangent of θ by
. For angles that are greater than 90° we define the tangent of θ by
![]() tan θ =
tan θ = 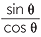 ,
,
unless cos In this case, we say that the tangent ratio is undefined. Between 0° and 360°, this will happen when θ = 90°, or θ = 270°. You will see in the following exercise why this is the case.
Note that this is the same as saying that tan θ equals the  .
.
EXERCISE 1
Place the point P on the unit circle corresponding to each of the angles 0°, 90° , 180°, 270°. By considering the coordinates of each such point, complete the table below
| P | θ | sin θ | cos θ | tan θ |
| 0° | ||||
| 90° | undefined | |||
| 180° | ||||
| 270° | undefined | |||
| 360° |
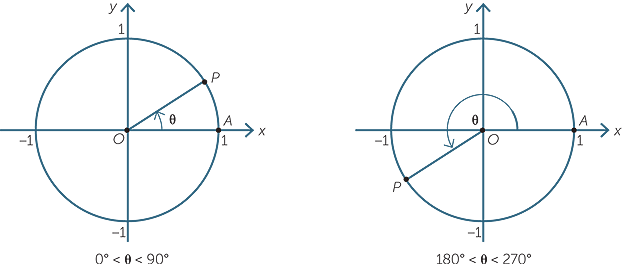
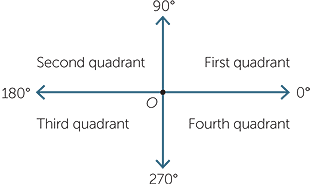
The coordinate axes divide the plane into four quadrants, labeled First, Second, Third and Fourth as shown. Angles in the third quadrant, for example, lie between 180° and 270°.
By considering the x and y coordinates of the point P as it lies in each of the four quadrants, we can identify the sign of each of the trigonometric ratios in a given quadrant. These are summarised in the following diagrams.
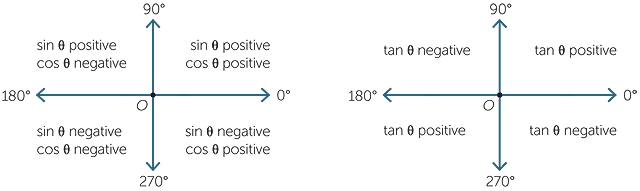
To obtain the second diagram, we used the definition tan θ = 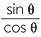 .
.
To assist in remembering the signs of the three trigonometric ratios in the various quadrants, we see that only one of the ratios is positive in each quadrant. Hence we can remember the signs by the picture:
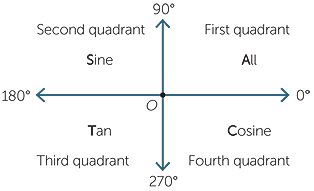
The mnemonic All Stations To Central is sometimes used.
EXAMPLE
What is the sign of
a![]() cos 150°
cos 150° ![]() b
b![]() sin 300°
sin 300° ![]() c
c![]() tan 235°?
tan 235°?
Solution
a![]() 150° lies in the second quadrant so cos 150° is negative.
150° lies in the second quadrant so cos 150° is negative.
b![]() 300° lies in the fourth quadrant so sin 300° is negative.
300° lies in the fourth quadrant so sin 300° is negative.
c![]() 235° lies in the third quadrant so tan 235° is positive.
235° lies in the third quadrant so tan 235° is positive.
The related angle
To find the trigonometric ratio of angles beyond 90°, we introduce the notion of the related angle. We will examine this quadrant by quadrant.
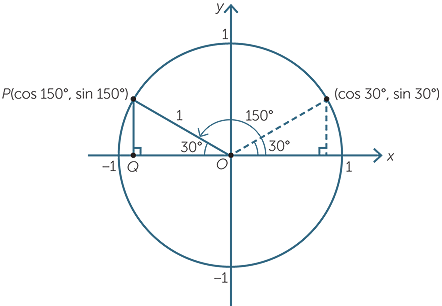 The Second Quadrant
The Second Quadrant
Suppose we wish to find the exact°and sin 150°.
The angle 150° corresponds
to the point P in the second quadrant with coordinates
(cos 150°, sin 150°) as shown.
The angle POQ is 30° and is called the related angle for 150°. From  POQ we can see that OQ = cos 30° and PQ = sin 30°, so the coordinates of P are −cos 30°, sin 30°).
POQ we can see that OQ = cos 30° and PQ = sin 30°, so the coordinates of P are −cos 30°, sin 30°).
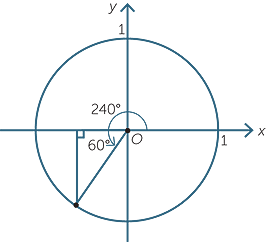
| Hence | cos 150° = −cos 30° = −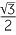 and sin 150° = sin 30° = and sin 150° = sin 30° =  . . |
|
| Also, | tan 150° = 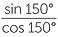 = −tan 30° = − = −tan 30° = − . . |
In general, if θ lies in the second quadrant, the acute angle 180° − θ is called the related angle for θ.
We introduced this idea in the module, Further Trigonometry.
The Third Quadrant
An angle between 180° and 270°
will place the corresponding point P in the third quadrant. In this quadrant, we can see that the sine and cosine ratios are negative and the tangent ratio positive.
To find the sine and cosine of 210° we locate the corresponding point P in the third quadrant. The coordinates of P are (cos 210°, sin 210°). The angle POQ is 30° and is called the related angle for 210°.
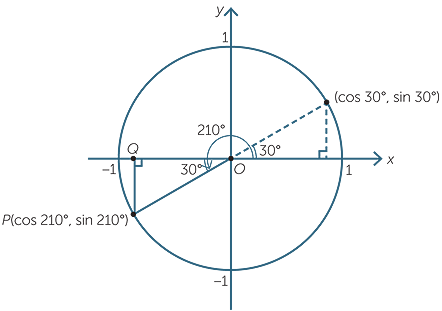
| So, |
cos 210° = −cos 30° = −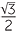 and sin 210° = −sin 30° = − and sin 210° = −sin 30° = − . . |
|
| Hence |
tan 210° = tan 30° = 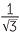 . . |
In general, if lies in the third quadrant, the acute angle θ − 180° is called the related angle for θ.
The Fourth Quadrant
Finally, if θ lies between 270° and 360° the corresponding point P is in the fourth quadrant. In this quadrant, we can see that the sine and tangent ratios are negative and the cosine ratio is positive.
To find the sine and cosine of 330° we locate the corresponding point P in the fourth quadrant. The coordinates of P are (cos 330°, sin 330°) .The angle POQ is 30° and is called the related angle for 330°.
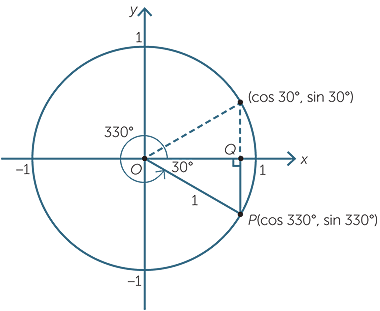
| So, |
cos 330° = cos 30° = 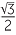 and sin 330° = −sin 30° = − and sin 330° = −sin 30° = − . . |
|
| Hence, |
tan 330° = −tan 30° = − . . |
In general, if lies in the fourth quadrant, the acute angle is called the related angle for θ.
In summary, to find the trigonometric ratio of an angle between 0° and 360° we
- find the related angle,
- obtain the sign of the ratio by noting the quadrant,
- evaluate the trigonometric ratio of the related angle and attach the appropriate sign.
EXAMPLE
Use the related angle to find the axact value of:
a![]() sin 120°
sin 120° ![]() b
b![]() cos 150°
cos 150° ![]() c
c![]() tan 300°
tan 300° ![]() d
d![]() cos 240°
cos 240°
Solution
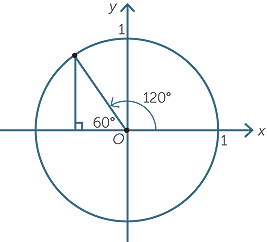
| a | The related angle is 60°. | ||
| 120° is in the second quadrant, | |||
| so sin 120° | = sin 60° |
||
= 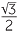 . . |
|||
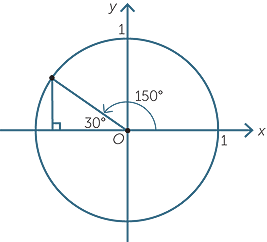
| b | cos 150° | = −cos 30° | |
= −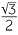 |
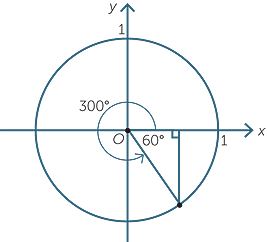
| c | tan 300° | = −tan 60° | |
= −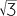 |
| d | cos 240° | = −cos 60° | |
= − |
Note that a calculator can be used to find, for example, including the correct sign.
The calculator is, however, of limited use in finding angles and for solving trigonometric equations. Here a thorough understanding of the above material is required.
EXERCISE 2
a![]() Find the exact value of
Find the exact value of
![]() i
i![]() sin 210°
sin 210° ![]() ii
ii![]() cos 330°
cos 330° ![]() iii
iii![]() tan 150°
tan 150°
b![]() Use your calculator to find cos 110° + cos 70°. Explain the answer.
Use your calculator to find cos 110° + cos 70°. Explain the answer.
We have previously defined the reciprocal ratios for angles between 0° and 90°.
We can extend these definitions to include any angles, so that
![]() cosec θ =
cosec θ = 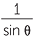 , for sin θ ≠ 0,
, for sin θ ≠ 0,
![]() sec θ =
sec θ = 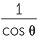 , for cos θ ≠ 0,
, for cos θ ≠ 0,
![]() cot θ =
cot θ =  , for tan θ ≠ 0.
, for tan θ ≠ 0.
EXERCISE 3
Find the exact value of
a![]() cosec 45°
cosec 45° ![]() b
b![]() cot 210°
cot 210°
c![]() sin2 120°cosec 270° − cos2 315°sec 180° − tan2 225°cot 315°.
sin2 120°cosec 270° − cos2 315°sec 180° − tan2 225°cot 315°.
As before, we take the point P on the unit circle. We have seen what happens as the point P moves through the four quadrants in an anti-clockwise direction. If the point continues a little further, it arrives back in the first quadrant.
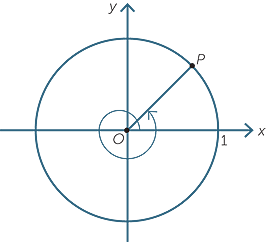
The angle shown is now greater than 360°. The point P, however, is back in the first quadrant. By considering the coordinates of P, we see that adding 360° to the angle does not change the x and y coordinates of P. Hence, for any θ,
| sin (360° + θ) = sin θ and cos (360° + θ) = cos θ | ||
| and so | tan (360° + θ) = tan θ. |
It is important to emphasise that although, for example, angles measuring 60° and 420° have the same sine, cosine and tangent ratios, they are different angles. They correspond to the same point on the unit circle, but are different angles.
We usually measure angles in an anti-clockwise direction and call them positive angles. Angles measured in a clockwise direction are called negative angles.
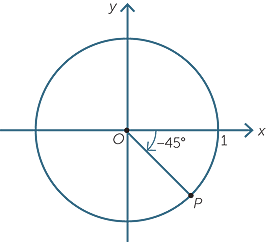
The diagram shows an angle of −45°.
EXAMPLE
Find sin 480° in surd form.
Solution
| sin 480° | = sin (480° − 360°) | ||
| = sin 120° | (120° lies in the second quadrant) |
||
| = sin 60° | (the related angle is 60°) | ||
= 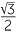 |
|||
EXAMPLE
Find cos (−120°) in surd form.
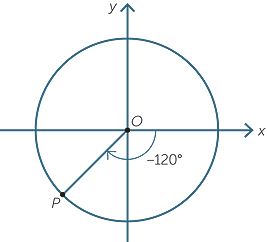 Solution
Solution
| cos (−120)° | = cos (−120° + 360°) | |
| = cos 240° | (240° lies in the third quadrant) |
|
| = −cos 60° | (the related angle is 60°) | |
=  |
||
EXERCISE 4
Find the exact value of sin 1200°.
In this section we will, unless stated otherwise, restrict our angles to be between 0° and 360°.
We have seen, for example, that the angles 30° and 150° have the same sine ratio  . Hence, if we ask the question: What angle has a sine of
. Hence, if we ask the question: What angle has a sine of  ? There are two answers.
? There are two answers.
The calculator can only give at most one of the two correct values.
Since we know the trigonometric ratios of the special angles 30°, 45° and 60°, these make good examples to practice on.
EXAMPLE
Find all angles in the range 0° to 360° such that
a![]() cos θ = −
cos θ = −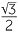
b![]() tan θ = −1.192
tan θ = −1.192 ![]() (give the answer to the nearest degree).
(give the answer to the nearest degree).
Solution
- a
- We recognise the number
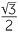 as the cosine of 30°. This is the related angle in this instance.
as the cosine of 30°. This is the related angle in this instance.
The negative sign tells us that the angle
is in the second or third quadrant.
Hence θ = 180° − 30° = 150° or
θ = 180° + 30° = 210°.
That is, θ = 150° or 210°.

- b
- We begin by finding the related angle, which we obtain from the calculator
by entering tan−1 1.192. This produces the related angle 50° (to the nearest degree).
Now the negative sign tells us that the angle lies in the second or fourth quadrants. Hence, to the nearest degree,
θ = 180° − 50° = 130° or θ = 360° − 50° = 310°.
That is, θ ≈ 130° or 310°.
Note then that we find the related angle by entering tan−1 1.192 into the calculator. If we enter tan−1 −1.192 the calculator may produce 130°, or on most calculators −50°, neither of which is all that helpful in finding the two desired solutions.
It is best to tell students not to enter on their calculator the inverse trigonometric function of a negative number.
EXERCISE 5
Solve the equation sin θ = −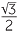 in the range, 0° ≤ θ ≤ 720°.
in the range, 0° ≤ θ ≤ 720°.
The trigonometric functions and their symmetries
We will now think of the trigonometric ratios as functions. Thus, the function y = sin θ has input values θ, consisting of angles, initially in the range 0° to 360°, and output values that are real numbers between −1 and 1.
In the module on The Quadratic Function, we saw how to draw the graph representing the points that lie on the parabola y = x2. Initially this was done by drawing up a table of ordered pairs, plotting them and connecting them to produce a smooth curve.
We can perform a similar task for the trigonometric functions y = cos θ and y = cos θ.
The graph of y = sin θ
Using the values sin 30° =  = 0.5 and sin 60° =
= 0.5 and sin 60° = 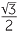 ≈ 0.87, we can draw up the following table of values and then plot them.
≈ 0.87, we can draw up the following table of values and then plot them.
| θ° |  |
0 |  |
30 |  |
60 |  |
90 |  |
120 |  |
150 |  |
180 |  |
210 |  |
240 |  |
270 |  |
300 |  |
330 |  |
360 |
| sin θ | 0 | 0.5 | 0.87 | 1 | 0.87 | 0.5 | 0 | −0.5 | −0.87 | −1 | −0.87 | −0.5 | 0 | |||||||||||||
More points can be used to show that the shape of the graph is as shown below.
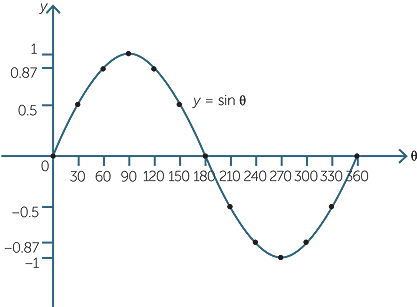
Electrical engineers and physicists call this a sinewave.
You can see many interesting symmetries in the graph of .
The model employing the unit circle helps to elucidate these. The sine of the angle θ is represented by the y-value of the point P on the unit circle. Thus, since sin θ = sin (180 − θ), we mark the two equal intervals in the graph.

Hence, between 0° and 180°, the graph is symmetric about θ = 90°.
Similarly, between 180° and 360°, the graph is symmetric about θ = 270°.
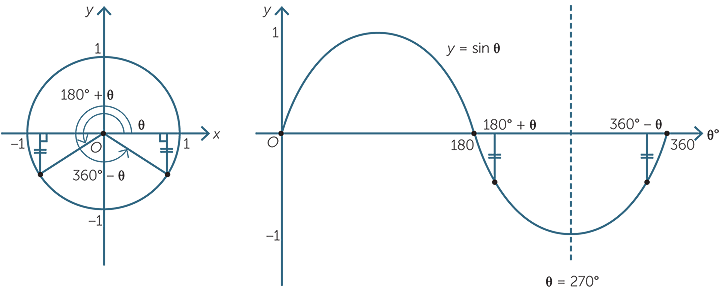
Finally, the graph possesses a rotational symmetry about θ = 180° as the following diagrams demonstrate.
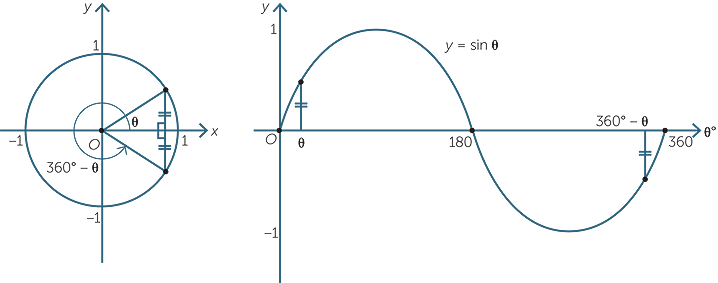
All these observations are summarised by the diagram:
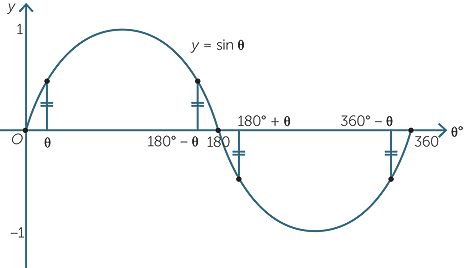
This symmetry diagram illustrates the related angle, the quadrant sign rules and the symmetries discussed above.
Extending the graph
We noted above that the values of sine repeat as we move through an angle of 360°, that is, sin (360° + θ) = sin θ . We say that the function y = sin θ is periodic with period 360°. Thus, the graph may be drawn for angles greater than 360° and less than 0°, to produce the full (or extended) graph of y = sin θ.
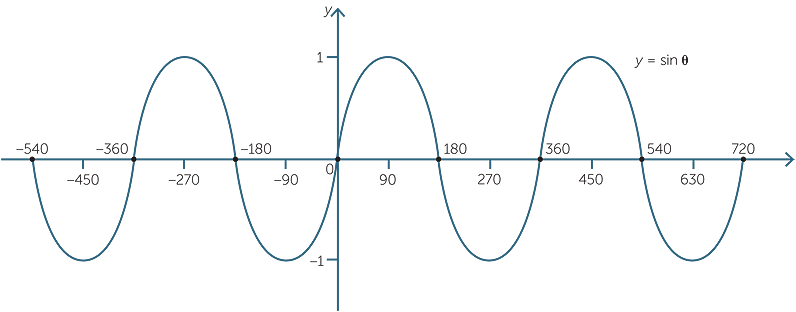
Note that the extended sine graph has even more symmetries. There is a translation (by 360°) symmetry, a reflection symmetry about any odd multiple of 90° and a rotational symmetry about vertical lines through any even multiple of 90°.
EXERCISE 6
- a
- Make up a table of values (to 2 dec. places) for y = cos θ similar to that shown for
y = sin θ. - b
- Plot the points in the table and sketch the graph of y = cos θ for θ in the range
0° to 360°. - c
- Mark in the symmetries for the graph in b
- d
- Draw the extended graph of y = cos θ.
- e
- In the extended graph of y = cos θ what are the points of rotational symmetry and the lines of reflection symmetry?
Note that if we translate the extended graph of y = cos θ by 90° to the right, we obtain the graph of y = sin θ.
In various modules we have looked at how to solve linear equations, such as 3x − 7 = 8 and quadratic equations such as x2 − 5x + 6 = 0. We have also seen that such equations naturally arise in problem solving.
Similarly trigonometric equations naturally arise in problem solving. An equation such as 2 sin x − 1 = 0 is an example of a linear trigonometric equation, since putting a = sin x produces the linear equation 2a − 1 = 0. Equations such as these generally have infinitely many solutions, but in practice we often restrict the range of solutions to be between 0° and 360°, or for example between −180° and 180°.
We can solve this equation by firstly making sin x the subject and then, using the methods outlined above, find all solutions in the range 0° ≤ x ≤ 360°.
| 2 sin x − 1 | = 0 | |
| sin x | =  |
|
| x | = 30°, 150° |
An equation such as 2cos2 x − 5cos x − 3 = 0 resembles a quadratic equation.
We can solve this for 0° ≤ x ≤ 360°, by putting a = cos x, thereby turning the equation
into a quadratic.
![]() 2cos2 x − 5cos x − 3 = 0
2cos2 x − 5cos x − 3 = 0
| Let | a | = cos x. | |||||
| Hence, | 2a2 − 5a − 3 | = 0 | |||||
| (2a − 1)(a + 3) | = 0 | ||||||
| a | =  , , |
a = −3 | |||||
| Thus | cos x | =  |
or | cos x = −3. | |||
The second equation has no solutions since −1 ≤ cos x ≤ −1. The first equation has solutions x = 60°, x = 300°.
EXERCISE 7
Use the identity cos2 x + sin2 x = 1 to find all solutions, in the range 0° ≤ x ≤ 360° for the equation sin2 x − cos2 x = 1.
In all of our work on trigonometry and geometry, we have measured angles in degrees. This is the traditional unit of measurement in geometry and introductory trigonometry which was inherited from the Babylonians. It is, however, an arbitrary unit of angle measure − one can also measure angles in a decimal system in which a right-angle is 100 units, (known as grads).
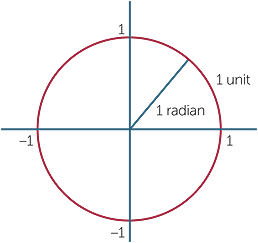
When we come to apply calculus to the trigonometric functions, it is more useful to provide a purely geometric procedure to measure an angle. This is done using the circumference of a unit circle.
We take a circle of radius 1 and define 1 radian to be the angle subtended by an arc of
1 unit on the circumference of the circle.
Now since the entire circumference has length 2π, and this subtends an angle of 360°,
we see that
![]() 2π radians equals to 360° or π radians are equal to 180°.
2π radians equals to 360° or π radians are equal to 180°.
Now the number π is approximately, 3.14159 correct to 5 decimal places, so we can divide and say that 1 radian is approximately 57.29578 degrees, which is 57 degrees, correct to the nearest degree.
EXERCISE 8
Express each of the angles: 30°, 45°, 60°, 90°, 225° as rational multiples of π.
Measuring angles in this way, it can be shown, by means of ratios, that in a circle of radius r the length ![]() of an arc subtending an angle θ measured in radians, is given by
of an arc subtending an angle θ measured in radians, is given by
![]() = rθ.
= rθ.
(Note that if θ is in degrees, ![]() =
= 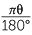 .)
.)
Furthermore, the area of the sector in this circle making an angle θ, again in radians,
at the centre, is given by
Area =  r2θ
r2θ
We saw above that the graphs of the functions y = sin θ and y = cos θ look like waves.
In the same way that a parabola (upside down) can be used to model projectile motion, so the trigonometric functions with radians can be used to model wave motion. Thus the function y = cos t might be used to model the vertical displacement of a point travelling on a wave at time t. We can obtain the velocity of the particle by taking the derivative.
It turns out that the derivative of sin t is cos t. This is remarkably simple!
Suppose that a mass is placed on the end 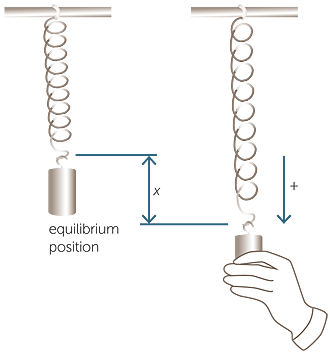
of a spring, pulled down and released. The
mass will oscillate about a central point.
simple harmonic motion.
If we plot the vertical displacement of the
mass from the central point, at time t, we
obtain a graph that is modeled by using
the sine curve.
Many physical phenomena can be modelled
using simple harmonic motion − for example sound waves and radio waves − and hence by the trigonometric functions.
The early history of trigonometry was covered in the modules, Introductory Trigonometry, and Further Trigonometry.
The history of the trigonometric functions really begins after the development of the calculus and was largely developed by Leonard Euler (1707−1783). The works of James Gregory in the 17th century and Colin Maclaurin in the 18th century led to the development of infinite series expansions for the trigonometric functions, such as
sin θ = θ − 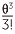 +
+ 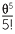 −
−  + ...
+ ...
This enabled accurate tables of values to be tabulated for the trigonometric functions and also useful approximations to be made. For example, when a pendulum is swung, since the angle θ between the arm of the pendulum and the vertical is small, physicists approximate sin θ by θ in the equation of motion and can thereby predict, approximately, the period of the pendulum.
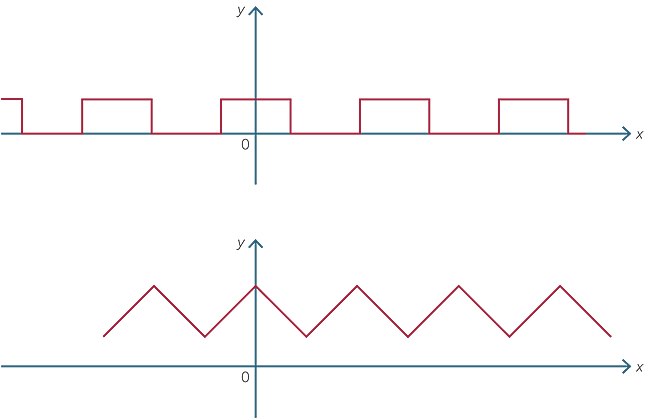
The mathematician Joseph Fourier (1768 − 1830) used infinite series of sines and cosines to solve problems involving heat transfer and vibrations. Thus the modern theory of Fourier Series was born. Any periodic function (that is, a function whose graph repeats after a fixed interval, called the period of the function) can be approximated by taking a series of trigonometric functions. Thus, for example, a square wave, and the so-called saw-tooth function, both of which arise in signal processing, can also be modelled using Fourier Series.
EXERCISE 1
| θ | sin θ | cos θ | tan θ |
| 0° | 0 | 1 | 0 |
| 90° | 1 | 0 | undefined |
| 180° | 0 | −1 | 0 |
| 270° | −1 | 0 | undefined |
| 360° | 0 | 1 | 0 |
EXERCISE 2
a![]() −
−
![]() b
b![]()
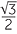
![]() c
c![]() −
−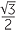
![]() d
d![]() cos 110° = −cos 70°
cos 110° = −cos 70°
EXERCISE 3
a![]()
![]()
![]() b
b![]()
![]()
![]()
![]() c
c![]()

EXERCISE 4
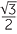
EXERCISE 5
240°, 300°, 600°, 660°
EXERCISE 7
90°, 270°
EXERCISE 8
a![]()
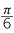
![]() b
b![]()
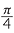
![]() c
c![]()
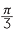
![]() d
d![]()
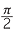
![]() e
e![]()
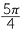
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

