The Improving Mathematics Education in Schools (TIMES) Project
Introductory Trigonometry
Measurement and Geometry : Module 23![]() Year : 9-10
Year : 9-10
June 2011
- Familiarity with Pythagoras’ theorem.
- Basic knowledge of congruence and similarity of triangles.
- Knowledge of the basic properties of triangles, squares and rectangles.
- Facility with simple algebra and equations.
- Familiarity with the use of a calculator.
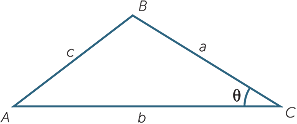
The word trigonometry signifies the measurement of triangles and is concerned with the study of the relationships between the sides and angles in a triangle. We initially restrict our attention to right-angled triangles.
Trigonometry was originally developed to solve problems related to astronomy, but soon found applications to navigation and a wide range of other areas. It is of great practical importance to builders, architects, surveyors and engineers and has many other applications.
Suppose we lean a ladder against a vertical wall. By moving the ladder closer to the wall, thereby increasing the angle between the ladder and the ground, we increase the distance up the wall that the ladder can reach. Since the length of the ladder remains the same, Pythagoras’ theorem relates the distance up the wall to the distance of the ladder from the base of the wall. Trigonometry allows us to relate that same distance to the angle between the ladder and the ground.
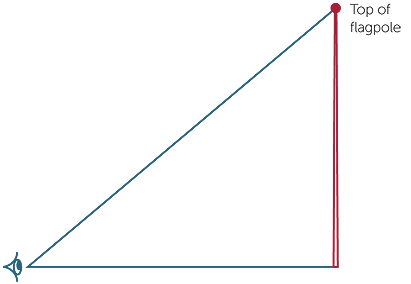
To measure the height of a flagpole, an observer can measure a distance out from the base and the angle made between the top of the pole and observer’s eye as shown in
the diagram.
As with many topics in Mathematics, trigonometry is a subject which continues on into the senior years of secondary school and well beyond into higher mathematics. Modern telecommunications depend on an understanding and harnessing of signal processing, which is modelled by the trigonometric functions.
Each right-angled triangle contains a right angle. The congruence tests tell us that
if either of the following pieces of information is known, then the triangle is
completely determined:
- one other angle and one side (by the ASA congruence test)
- two sides (by either the SAS test or the RHS test).
Trigonometry and Pythagoras’ theorem enable us to find the remaining sides and angles in both cases.
If we have two similar right-angled triangles (sometimes called right triangles), then the angles of one match up with the angles of the other and their matching sides are in the same ratio.
For example, the following triangles are similar.
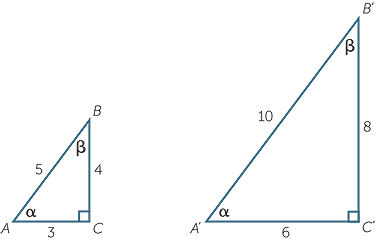
Since the matching sides are in the same ratio,
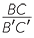 = = 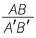 = = 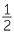 . . |
This means that the ratio
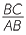 = = 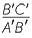 = = 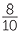 = = 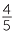 . . |
Similarly, the ratio
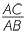 = = 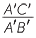 = = 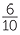 = = 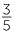 |
|
| and | 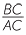 = = 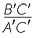 = = 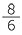 = = 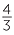 . . |
That is, once the angles of a triangle are fixed, the ratios of the sides of the triangle are constant. In a right-angled triangle, we only need to know one other angle and then the angle sum of a triangle gives us the third angle. Hence, in a right-angled triangle, if we know one other angle, then the ratios of the sides of the triangle are constant.
This is the basis of trigonometry.
EXERCISE 1
Draw up an angle of 58° using a protractor. Place markers at distances of 3cm, 5cm and 8cm and draw perpendiculars as shown in the diagram.
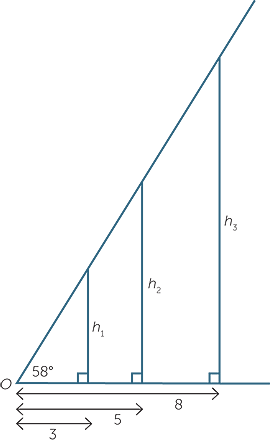
Measure the heights marked, h1, h2, h3 and calculate to one decimal place the ratios ![]() ,
, ![]() ,
, ![]() .
.
Why are the ratios (approximately) equal ?
Naming the sides
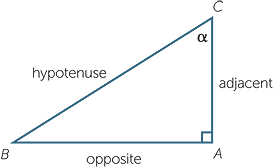
In order to distinguish the various possible ratios in a right-angled triangle, we introduce some names. We always refer to the longest side (opposite the right-angle) as the hypotenuse.
We now choose one of the two acute angles and label it, often using one of the Greek letters α, β, ![]() or θ. We shall call this angle the reference angle.
or θ. We shall call this angle the reference angle.
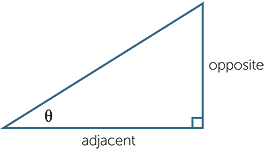
The side opposite the reference angle is called the opposite side, generally referred to as the opposite, and the remaining side is called the adjacent side, or simply adjacent, since it is next to the reference angle.
As mentioned above, once we fix the size of the reference angle in a right-angled triangle then the ratios of various sides remain the same irrespective of the size of the triangle. There are six possible trigonometric ratios we could use. We mainly work with just three of them. The remaining three are their reciprocals.
The ratio of the opposite to the adjacent is known as the tangent ratio or the tangent of the angle θ. (The name comes from an earlier time and involves the use of circles.) We write
tan θ =  |
where | 0° < θ < 90°. |
EXAMPLE
Write down the value of tan θ.
| a |  |
b | 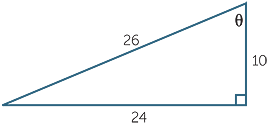 |
Solution
| a | tan θ = 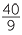 |
b | tan θ | = 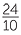 |
|||
= 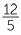 |
EXERCISE 2
By drawing an appropriate triangle explain why tan 45° = 1
From the first exercise above, you will have found that the ratios 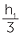 ,
, 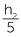 ,
, 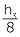 were all approximately 1.6. These ratios correspond to a tangent ratio, so tan 58° is approximately 1.6. The calculator gives tan 58° ≈ 1.6000334529...
were all approximately 1.6. These ratios correspond to a tangent ratio, so tan 58° is approximately 1.6. The calculator gives tan 58° ≈ 1.6000334529...
The tangent ratio for other angles can be found using a calculator. Needless to say the calculator does not ‘draw a triangle’ but uses clever mathematical algorithms to find the value. It is important that students make sure their calculator is in degree mode.
We can use the tangent ratio to calculate missing sides in a right-angled triangle, provided we are given the right information.
EXAMPLE
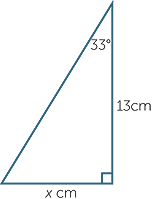
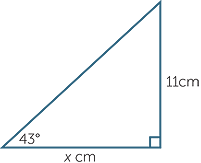
| a | Find the length marked x in the diagram below, correct to two decimal places. |
b | Find x, correct to two decimal places | |||
 |
 |
Solution
| a | tan 33° | =  |
b | tan 43° | = 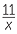 |
|||||||
| Hence | x | = 13 tan 33° | Hence | x tan 43° | = 11 | |||||||
| ≈ 8.44 | so | x | = 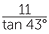 |
|||||||||
| ≈ 11.80 |
The Three BASIC Trigonometric Ratios
In addition to the tangent ratio, there are two other basic ratios that we use.
These are known as the sine and cosine ratios. We take θ to be the reference angle
so 0° < θ < 90°. The three ratios are defined by:
sin θ =  ,
, ![]() cos θ =
cos θ =  ,
, ![]() tan θ =
tan θ = 
Students need to learn these definitions thoroughly. One simple mnemonic that might assist them is SOH CAH TOA, consisting of the first letter of each ratio and the first letter of the sides making up that ratio.
EXAMPLE
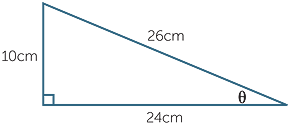 For the following triangle, write down the value of:
For the following triangle, write down the value of:
| a | sin θ | b | cos θ | c | tan θ |
Solution
| a | sin θ | =  |
b | cos θ | =  |
c | tan θ | = 
|
|||||
= 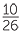 |
= 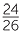 |
= 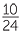 |
|||||||||||
= 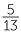 |
= 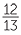
|
= 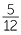 |
The angles 30°, 45° and 60° appear frequently in trigonometry and their sine, cosine and tangent ratios can be expressed using rational numbers and surds.
EXERCISE 3
In the diagrams below, calculate all sides and angles and then fill in the table below.

| θ | 30° | 45° | 60° |
| sin θ | |||
| cos θ | |||
| tan θ |
We can use the trigonometric ratios to calculate missing sides in a right-angled triangle.
EXAMPLE
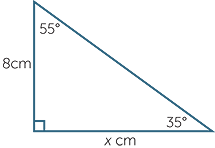
Find the value of x, correct to four decimal places.
| a |  |
b | 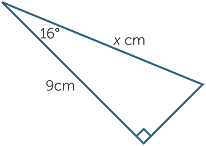 |
|||
| c | 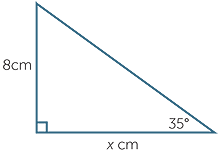 |
Solution
| a | This problem involves opposite and hypotenuse, so use sine. | b | This problem involves adjacent and hypotenuse, so use cosine. | ||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
| c | This problem involves adjacent and opposite, so use tangent. | |||||||||||||||||||||||||||||||||||
|
 |
|||||||||||||||||||||||||||||||||||
EXERCISE 4
Suppose that 0° < θ < 90°.
a![]() Explain why sin (90° − θ) = cos θ, and simplify cos (90° − θ).
Explain why sin (90° − θ) = cos θ, and simplify cos (90° − θ).
b![]() Prove that
Prove that 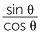 = tan θ.
= tan θ.
c![]() It is standard notation to write (sin θ)2 as sin2 θ, and (cos θ)2 as cos2 θ.
It is standard notation to write (sin θ)2 as sin2 θ, and (cos θ)2 as cos2 θ.
Prove that cos2 θ + sin2 θ = 1.
d![]() Explain why 0 < cos θ < 1 and 0 < sin θ< 1.
Explain why 0 < cos θ < 1 and 0 < sin θ< 1.
We have seen that in any right-angled triangle with reference angle θ, there are three basic ratios associated with that angle and that the value of each ratio can be found using a calculator. In order to use the trigonometric ratios to find angles in a right-angled triangle, we need to reverse the process. Thus, given the sine, cosine or tangent of some angle between 0 and 90 degrees, we want to find the angle with the given ratio.
We have seen that tan 45° = 1. We say that the inverse tangent of 1 is 45°. This is written as tan-1 1 = 45°.
Students must not confuse this −1 index with its usual algebraic meaning of ‘one over’.
To help avoid this, it is best to read the symbol tan-1 as inverse tangent and not as tan to the minus one.
Similarly, since sin 30° = 0.5, we write sin-1 0.5 = 30° and say: the inverse sine of 0.5 is 30°.
To find, for example, cos-1 0.25, we use the calculator, which gives 75.52°, correct to two decimal places.
EXAMPLE
Find each of the following, correct to the nearest degree.
| a | sin-1 0.6 | b | cos-1 0.412 | c | tan-1 2 | |||||
| d | the angle θ for which sin θ = 0.8 | e | the angle θ for which cos θ = 0.2 | |||||||
Solution
By calculator.
| a | sin-1 0.6 | = 36.86989...° | b | cos-1 0.412 | = 65.66946...° | |||||
| ≈ 37° | ≈ 66° | |||||||||
| c | tan-1 2 | = 63.43494...° | d | If | sin θ | = 0.8 | ||||
| ≈ 63° | then | θ | = sin-1 0.8 | |||||||
| = 53.13...° | ||||||||||
| ≈ 53° | ||||||||||
| e | If | cos θ | = 0.2 | |||||||
| then | θ | = cos-1 0.2 | ||||||||
| = 78.463...° | ||||||||||
| ≈ 78° | ||||||||||
The following exercise shows us how to find an angle from two given sides.
EXERCISE 5
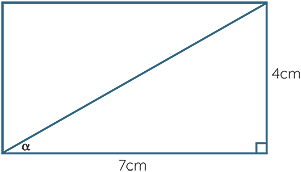
- a
- Find the angle between the diagonal and the base of the rectangle, correct to the nearest degree.
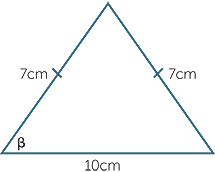
- b
- Find the base angle in the isosceles triangle,
correct to the nearest degree.
Angles of Elevation and Depression
When an observer looks at an object that is higher than the (eye of) the observer, the angle between the line of sight and the horizontal is called the angle of elevation.
On the other hand, when the object is lower than the observer, the angle between the horizontal and the line of sight is called the angle of depression. These angles are always measured from the horizontal.
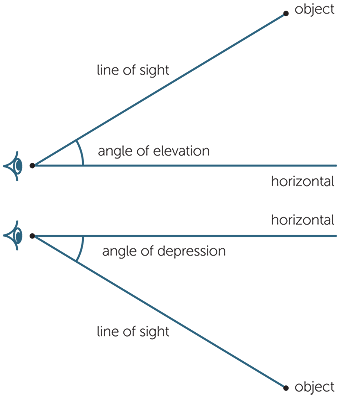
EXAMPLE
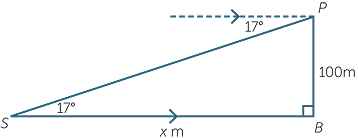
From the top of a cliff, 100 m above sea level, the angle of depression to a ship sailing past is 17°. How far is the ship from the base of the cliff, to the nearest metre?
Solution
The diagram shows the top of the cliff P, the ship S and the base of the cliff B.
Let SB = x m be the distance of the ship from the cliff. By alternate angles, ![]() PSB = 17°.
PSB = 17°.
| Hence | tan 17° | = 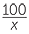 |
|
| so | x | = 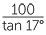 |
|
| = 327.085 |
The distance is 327 m (to the nearest metre).
In some problems several steps may be required to find the desired lengths.
EXAMPLE
From a point A, 10 m from the base of a tree, the angle of elevation of the top of a tree is 36°. From a point B, x m further on from the base of the tree, the angle of elevation is 20°.
a Find the height of the tree to the nearest tenth of a metre.
b Find the distance x m to the nearest tenth of a metre.
Solution
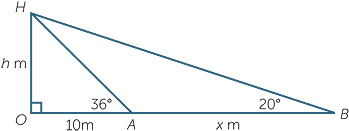
| a | Let the height of the tree be h metres | |||
In 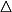 OHA, OHA,
|
tan 36° | = 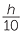 |
||
| so | h | = 10 tan 36° | ||
| = 7.2654... | ||||
| ≈ 7.3 m, to the nearest tenth of a metre | ||||
Note: The approximation 7.3 is not used in part b. It leads to the wrong answer.
| b | In 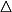 HOB, HOB, |
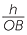 |
= tan 20° | |
| hence | OB | =  |
||
=  |
||||
| = 19.96... | ||||
| so | x | = AB | ||
| = OB − OA | ||||
| = 9.96... | ||||
| ≈ 10.0 m to the nearest tenth of a metre |
EXERCISE 6
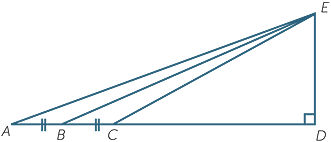 Consider the diagram shown opposite.
Consider the diagram shown opposite.
a![]() Prove that BD =
Prove that BD = 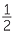 (AD + CD).
(AD + CD).
b![]() Hence deduce that
Hence deduce that
tan ![]() DEB =
DEB = 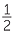 tan
tan ![]() AED +
AED + 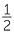 tan
tan ![]() CED
CED
One of the early applications of trigonometry was to improve navigation. Bearings are used to indicate the direction of an object (perhaps a ship) from a fixed reference point (perhaps a light house). True bearings give the angle θ° from the north measured clockwise. We write the true bearing of θ° as θ° T, where θ° is an angle between 0° and 360°. It is customary to write the angle using three digits, so 0° T is written as 000° T, and a true bearing of 15° is written as 015° T.
We can use trigonometry to solve problems involving bearings.
EXAMPLE
Anthony walks for 490 metres on a bearing of 140° T from point A to point B.
Find to the nearest metre,
a how far east the point B is from the point A.
b how far south the point B is from the point A.
Solution
| a | Distance east | = 490 sin 40° | |
| ≈ 315 m (correct to the nearest metre) | |||
| b | Distance south | = 490 cos 40° | |
| ≈ 375 m (correct to the nearest metre) |
Navigational questions can also be given using compass bearings.
EXERCISE 7
From a point P, a ship sails N 20° E for 20km to the point Q. From Q the ship sails N 70° W until it is at the point R directly north of P. Find the distance PR.
If we take any triangle with two given sides a and b about a given (acute) angle , then the area of the triangle is given by
Area = 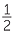 ab sin θ
ab sin θ
EXERCISE 8
By dropping an altitude in the triangle shown below, derive the formula stated above.
Note that the above formula works even in the case when θ is obtuse. In the module, Further Trigonometry, we will show how to define the sine of an obtuse angle.
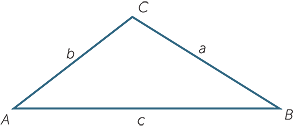
From the material developed so far it should be apparent that the trigonometric ratios are a powerful tool for relating angles and sides in right-angled triangles. Not all triangles, of course, possess a right angle. We can extend the angle/side connection to an arbitrary triangle using two basic formulas known as the sine rule and the cosine rule.
The sine rule states that in the triangle shown,
 =
= 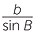 =
=  .
.
In words this says that in any triangle, any side divided by the sine of the opposite angle is equal to any other side divided by the sine of its opposite angle.
The cosine rule states that in the triangle shown
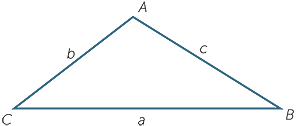 c2 = a2 + b2 − 2ab cos C.
c2 = a2 + b2 − 2ab cos C.
This may be thought of as Pythagoras’ theorem with a correction term.
You may care to derive these from the material established in this module. The sine rule is relatively easy to prove. For the cosine rule, drop a perpendicular from A and apply Pythagoras’ theorem to the two triangles. The details of the proofs are given in the module, Further Trigonometry and in the module, Pythagoras’ Theorem.
In general, a triangle may contain an obtuse angle as well as acute angles. Thus far we have only defined the trigonometric ratios for acute angles.
The trigonometric ratios can be extended to include obtuse angles and this will be done in the module, Further Trigonometry.
If θ is an obtuse angle then the sine of θ is given by
![]() sin θ = sin (180° − θ).
sin θ = sin (180° − θ).
Note that if θ is an obtuse angle, then its supplement, 180° − θ , is acute.
Similarly, if θ is an obtuse angle then the cosine of θ is given by
![]() cos θ = − cos (180° − θ),
cos θ = − cos (180° − θ),
and the tangent of θ is given by
![]() tan θ = − tan (180° − θ).
tan θ = − tan (180° − θ).
Thus, the sine of an obtuse angle equals the sine of its supplement and the cosine and tangent of an obtuse angle equal the negative of the cosine and tangent of its supplement, respectively.
In the module, Trigonometric Functions we extend the definitions even further to include all angles, including those greater than 180° and negative angles.
Once we are able to find the sine of all possible angles, we can plot the graph of the function
y = sin x. This leads us to study the trigonometric functions which are used to describe wave motion and electronic signal processing.
There are six possible ratios that one might take between the three sides of a right-angled triangle. We can take the reciprocal of the three ratios sine, cosine and tangent to produce the remaining three.
These ratios are called: cosecant, secant and cotangent respectively. These are written as
cosec θ, sec θ, and cot θ.
Thus, if 0° < θ < 90°,
cosec θ =  = =  , , |
sec = θ  = = 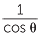 , , |
cot θ =  = = 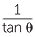 |
The prefix co- is short for complementary, since the cosine of an angle is equal to the sine of its complement. The cotangent of an angle is the tangent of its complement and similarly the cosecant of an angle is the secant of its complement.
We saw in the examples in this module, that we can get by with using only the sine, cosine and tangent ratios in problem solving. However, the reciprocal ratios arise naturally when we study the calculus of the trigonometric functions.
EXERCISE 9
Show that, if 0° < θ < 90°,
| a | 1 + tan2 θ = sec2 θ. | b | cot2 θ + 1 = cosec2 θ. |
The Plimpton 322 tablet, believed to have been written about 1800BC, contains a table of numbers in base 60 that are believed by some to be an early record of tangent ratios. This remains controversial.
The Greeks developed a form of trigonometry based on chords in a circle. Hipparchus of Nicaea (c. 180-125 BC), sometimes called `the father of Trigonometry’, came from near present day Istanbul. He was an astronomer and he was able to calculate the duration of the year to within 6 minutes. To assist with his astronomical calculations, he developed an early form of trigonometry and drew up tables of chords. This table was later extended, and used, by Ptolemy (c.90−160 AD).
Hipparchus divided the circumference of a circle into 360° (as the Babylonians had done) and the diameter into 120 parts.
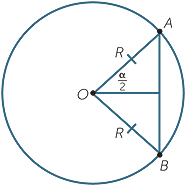
Then for a given arc AB subtending an angle  at the centre, he gives the length of the corresponding chord crd(
at the centre, he gives the length of the corresponding chord crd( ), as shown in the diagrams below.
), as shown in the diagrams below.
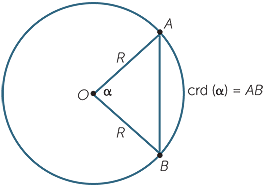
Note then that crd (60°) = R and also crd (90°) = ![]() R.
R.
The length of the chord is related to the sine ratio as the following diagram shows.
![]() AB = crd(
AB = crd( ) = 2R sin
) = 2R sin 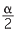 .
.
Hipparchus did his calculations with R = 60. Algebraic notation was not available at this time.
With the decline of civilisation in the West, Indian and Arab mathematicians built on the work of the Greeks. In about the 5th century AD, in a work known as Surya Siddhanta, a table of sines appeared. The Arabs also developed spherical trigonometry, again to be used in astronomy.
As we saw above, the sine is related to half a chord, and the word sine itself, arose from a series of mistranslations of a Sanskrit word for half-chord. The Indian word was transliterated into Arabic and then misunderstood as a word meaning breast. This in turn came to mean curve and hence bay or gulf which is sinus in Latin.
The motivation for much of early trigonometry was astronomy. The first pure trigonometrical text written in Europe was De triangulis Omnimodis (‘On all sorts of triangles’) by Johann Müller (1436 − 1476), alias Regiomontanus. His work was motivated by his translation of Ptolemy, in which he realised that a more systematic treatment of trigonometry was required. He wrote:
You who wish to study such great and wonderful things, who wonder at the
movement of the stars, must (first) read these theorems about triangles!
In his work, he derives and proves the sine rule.
The cosine was defined by cos θ = sin (90° − θ). This is the sine of the complement of the angle.
The terms tangent and secant were introduced by T. Fink (1561 − 1656) while cotangent, (the complement of the tangent), was introduced by by E. Gunther (1581 −1626).
The following diagram shows how the names tangent and secant arose:
![]()
![]()
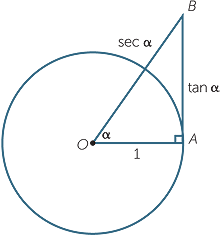
![]() AB = tan
AB = tan  , OB = sec
, OB = sec  .
.
If the radius of the circle is 1, then AB, which has length tan α, touches the circle at A
(Latin tango − I touch) and OB, which has length sec α, cuts the circle (Latin seco − I cut.)
Exercise 1
The right-angled triangles are similar to each other.
EXERCISE 2
Draw a right-angled isosceles triangle. The equal angles are each 45°.
Therefore tan 45° = 1.
EXERCISE 3
| θ |
30° |
45° |
60° |
| sin θ | 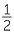 |
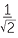 |
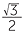 |
| cos θ | 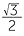 |
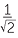 |
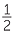 |
| tan θ | 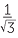 |
1 | 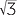 |
EXERCISE 4
a, b and c are the side lengths of triangle ABC. ![]() C = 90° and
C = 90° and ![]() A = θ°.
A = θ°.
a![]() sin θ =
sin θ = 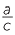 and cos B =
and cos B = 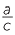 . But B = 90° − θ° . Therefore cos (90 − θ) = sin θ.
. But B = 90° − θ° . Therefore cos (90 − θ) = sin θ.
b![]() tan θ =
tan θ = 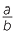 =
= 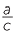 ÷
÷ 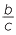 =
= 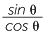 .
.
c![]() sin2θ + cos2θ =
sin2θ + cos2θ = 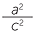 +
+ 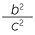 =
= 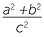 = 1
= 1
d![]() The hypotenuse is the longest side and so sin θ =
The hypotenuse is the longest side and so sin θ = 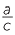 < 1 and cos θ =
< 1 and cos θ = 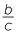 < 1.
< 1.
EXERCISE 5
a![]() 30°
30° ![]()
![]() b
b![]() 44°
44°
EXERCISE 6
| a | BD = AD − AB | |||
| BD = BC + CD | ||||
| Adding gives | 2BD = AD + CD | |||
BD = 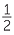 (AD + CD) (AD + CD) |
||||
| b | tan |
=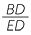 |
||
= 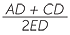 |
||||
= 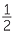 tan tan 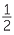 tan tan |
EXERCISE 7
21.28 km
EXERCISE 8
Draw BD perpendicular to AC with D on AC.
| Area | = 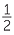 b × BD b × BD |
=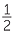 ab sin θ ab sin θ |
EXERCISE 9
sin2 θ + cos2 θ = 1
a![]() Divide both sides by cos2 θ to obtain the result.
Divide both sides by cos2 θ to obtain the result.
b![]() Divide both sides by sin2 θ to obtain the result
Divide both sides by sin2 θ to obtain the result
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


