The Improving Mathematics Education in Schools (TIMES) Project
- The content of the module Quadratic Equations.
- Familiarity with coordinate geometry
- Elementary graphs, including the graph of y = x2.
I am the very model of a modern Major-General,
I’ve information vegetable, animal, and mineral,
I know the kings of England, and I quote the fights historical,
From Marathon to Waterloo, in order categorical;
I’m very well acquainted too with matters mathematical,
I understand equations, both the simple and quadratical.
− Gilbert and Sullivan Pirates of Penzance.
The parabola is a curve that was known and studied in antiquity. It arises from the dissection of an upright cone.

With the advent of coordinate geometry, the parabola arose naturally as the graph of a quadratic function. The graph of the function y = mx + b is a straight line and the graph of the quadratic function y = ax2 + bx + c is a parabola. Since y = mx + b is an equation of degree one, the quadratic function, y = ax2 + bx + c represents the next level of algebraic complexity.
The parabola also appears in physics as the path described by a ball thrown at an angle to the horizontal (ignoring air resistance). The vertex of the parabola gives information regarding maximum height and combined with the symmetry of the curve also tells us how to find the horizontal range.
Quadratic functions frequently appears when solving a variety of problems. The theory of these functions and their graphs enables us to solve simple maximisation/minimisation problems without having to resort to calculus.
Their study in Year 10 gives an excellent introduction to important ideas that will be encountered in senior mathematics and beyond.
Students will be familiar from earlier years with the graph of the function y = x2 which they obtained by making up a table of values and plotting points. This graph is called a parabola. The path of a ball tossed under gravity at an angle to horizontal (roughly)
traces out a parabola.
For the sake of convenience we will refer to the graph of y = x2 as the basic parabola.
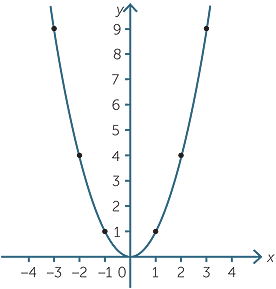
The basic parabola has a number of important properties.
- the graph is symmetrical about the y-axis. This means that the y-value at, say x = 3, is the same as the y-value at x = −3. The y-axis is called the axis of symmetry of the parabola.
- the minimum value of y occurs at the origin. This point is called the vertex of the parabola. It also represents the minimum value of the function, since the y-values to the right and left of this point are greater than the y-value at the origin.
- the arms of the parabola continue indefinitely, becoming steeper the higher they go.
This basic parabola can be reflected in vertical and horizontal lines and translated to produce congruent parabolas. It is also possible to reflect in other lines and rotate parabolas, but the corresponding algebra is difficult and is generally studied in later years using matrices.
Since each point on the basic parabola satisfies the equation y = x2 we can express the coordinates of the general point by (a, a2). Thus the value a = 2, gives the point (2, 4).
When the basic parabola y = x2 is reflected in the x-axis, the point (3, 9), for example, is reflected to the point (3, 9). Indeed the general point (a, a2) becomes (a, −a2) and so the equation satisfied by these points is y = −x2.
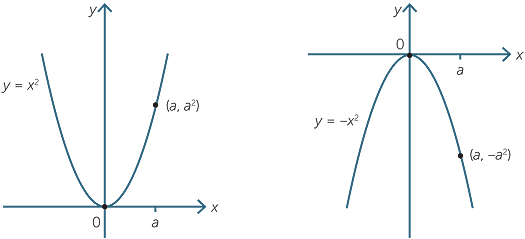
We can confirm this with a table of values.
Translations of the basic parabola
Vertical translation
When we translate the parabola vertically upwards or downwards, the y-value of each point on the basic parabola is increased or decreased. Thus, for example, translating the parabola upwards by 9 units, shifts the general point (a, a2) to (a, a2 + 9). The equation of this new parabola is thus y = x2 + 9. The vertex of this parabola is now (0, 9), but it has the same axis of symmetry. Similarly, the basic parabola becomes y = x2 − 9 when translated down 9 units, with vertex (0, 9).

We can confirm this with a table of values.
Horizontal translation
What happens when we translate the basic parabola to the left or to the right?
This is more tricky.
We begin by considering the equation y = (x − 3)2. Since the right-hand side is a square, the y-values are all non-negative and takes the value 0 when x = 3.
The value x = 5, which is 2 units to the right of 3, produces the same y value as does
x = 1, which is 2 units to the left of 3. Since the same thing will happen as we move the same number of units to the right or left of 3, we see that the graph of this function is symmetric about the line x = 3.
Thus x = 3 is the equation of the axis symmetry for this graph, which has its vertex at (3, 0).
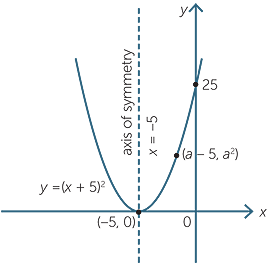
If we put x = 0 we obtain y = 9 and this is called the y-intercept.
The graph of y = (x − 3)2 is congruent to the basic parabola, but is translated 3 units to the right.

We can confirm this with a table of values.
Similarly, the graph of y = (x + 5)2 is congruent to the basic parabola, but is translated 5 units to the left. Its vertex is the point (−5, 0) and the axis of symmetry is x = −5.
EXERCISE 1
- a
- Write down the equation of the parabola obtained when the graph of y = x2 is translated 3 units to the left. Sketch the parabola.
- b
- Describe the transformation required to move the parabola y = (x + 3)2 to y = (x − 2)2 . Sketch the parabola.
General Translations
We can combine the two transformations and shift parabolas up or down and then left or right.
Thus, for example, the graph of the parabola with equation y = (x − 3)2 + 5 is congruent
to the basic parabola, with a shift to the right of 3 units and a shift upwards of 5 units.
The vertex is at (3, 5) and the axis of symmetry is x = 3.
We can find the y-intercept by putting x = 0 to give y = 14.
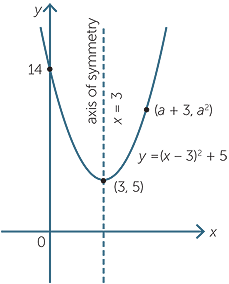
Finding the y-intercept is a useful thing to do and assists in drawing the diagram.
EXERCISE 2
Consider the parabola with equation y = (x + 2)2 − 4.
- a
- Describe how the graph of this parabola is obtained from the basic parabola.
- b
- State the vertex and the equation of the axis of symmetry of this parabola.
- c
- Sketch the parabola showing the y-intercept and the x-intercepts.
Sketching the graph of y = x2 + bx + c
We have seen that if a parabola is in the form y = (x − h)2 + d, then we can find its vertex, its axis of symmetry, and produce a sketch with little effort. Quadratic functions are, however, generally given in the expanded form y = x2 + bx + c. The technique of completing the square enables us the change the given equation to our desired form.
To complete the square, we add and subtract the square of half the coefficient of x.
Example
Complete the square and hence sketch the graph of y = x2 + 6x + 13.
Solution
| y | = x2 + 6x + 13 | ||
| = (x2 + 6x + 32) + 13 − 32 | (Add and subtract the square of half the coefficient of x.) | ||
| = (x2 + 6x + 9) + 13 − 9 | |||
| = (x + 3)2 + 4 |
Exercise 3
Sketch the following parabolas. First find the y-intercept, then complete the square to find the axis of symmetry and the vertex of the parabola, then find the x-intercepts if they exist.
a![]() y = x2 + 4x
y = x2 + 4x ![]() b
b![]() y = x2 − 6x
y = x2 − 6x ![]() c
c![]() y = x2 + x + 1
y = x2 + x + 1
x−intercepts
We have seen in the examples so far that some parabolas cut the x-axis and some do not. We can find the x-intercepts, if they exist, by setting y = 0 in the equation of the parabola. This will produce a quadratic equation. As discussed in the module, Quadratic equations, this can be solved in three ways:
- by factoring
- by completing the square
- by the quadratic formula.
Completing the square, which is often done to find the vertex and axis of symmetry anyway, is often the most efficient way of laying bare all of the features of the parabola.
For example, to analyse the graph of the quadratic function y = x2 + 4x − 5, we complete the square.
| y = x2 + 4x − 5 | |
| y = (x + 2)2 − 4 − 5 | |
| y = (x + 2)2 − 9 |
This tells us that the vertex is at (−2, 9) and the equation of the axis of symmetry is x = −2. To find the x-intercepts, we put y = 0 to obtain
| (x + 2)2 − 9 = 0 | |||||||
| (x + 2)2 = 9 | |||||||
| x + 2 | = 3 | or | x + 2 | = −3 | |||
| x | = 1 | or | x | = −5. | |||
This method will, of course, work even if the x-intercepts are surds.
Furthermore, when we complete the square on a parabola such as y = x2 − 4x + 6
we obtain y = (x − 2)2 + 2.
Since the right-hand side is always at least 2, the y-values are never zero. Thus this parabola has no x-intercepts.
EXERCISE 4
Sketch each parabola showing the intercepts, axis of symmetry and vertex.
a![]() y = x2 + 6x − 7
y = x2 + 6x − 7 ![]() b
b![]() y = x2 + 7x − 5
y = x2 + 7x − 5
Upside-down parabolas
We saw above that the parabola y = −x2 is the reflection of the basic parabola in the x-axis. Similarly, a parabola such as y = −(x − 4)2 is a reflection of the parabola y = (x − 4)2 in the x-axis.
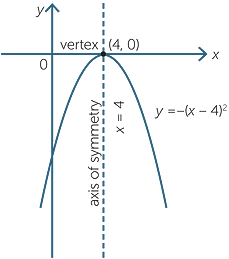
Once the basic parabola y = x2 is reflected to y = −x2, we can apply vertical and horizontal translations as discussed above.
Thus, for example, to graph the parabola with equation y = −(x − 4)2 + 7, we take the parabola y = x2 and:
| reflect in the x-axis | y = −x2 |
| translate 4 units to the right | y = (x − 4)2 |
| translate 7 units up | y = −(x − 4)2 + 7 |

EXERCISE 5
Sketch the graphs of the parabolas with equations:
a![]() y = −x2 − 8
y = −x2 − 8 ![]() b
b![]() y = −(x + 3)2 − 4
y = −(x + 3)2 − 4 ![]() c
c![]() y = −(x − 2)2 + 6
y = −(x − 2)2 + 6
The problem of completing the square for equations of upside-down parabolas is tricky. One approach is to take out a factor of − 1. We can then treat the quadratic in the brackets in the usual way.
EXAMPLE
Complete the square and hence sketch the graph of the parabola with equation
y = −x2 − 6x − 8.
Solution
Factor out −1, and obtain
y = −x2 − 6x − 8
y = −[(x + 3)2 − 9 + 8] ![]() (Complete the square)
(Complete the square)
y = −[(x + 3)2 − 1]
y = −(x + 3)2 + 1.
Hence the vertex is at (−3, 1). To find the x-intercepts, we set and so
| 0 | = −(x + 3)2 + 1 | ||||
| (x + 3)2 | = 1 | ||||
| x + 3 | = 1 | or | x + 3 | = −1 | |
| x | = −2 | or | x | = −4 | |
| When x = 0, y = −8. | |||||
The graph is drawn here.
![]()

Exercise 6
Sketch the following parabolas. In each case complete the square and determine the
x- and y-intercepts, the axis of symmetry and the vertex of the parabola.
a![]() y = −x2 + 8x + 13
y = −x2 + 8x + 13 ![]() b
b![]() y = −x2 − 3x − 5
y = −x2 − 3x − 5 ![]() c
c![]() y = −x2 − 10x
y = −x2 − 10x
The transformations dealt with so far have produced parabolas that are congruent to the basic parabola y = x2. There is a further transformation that results in stretching the arms of the parabola, producing a new parabola that is not congruent to the original one.
We begin by graphing the parabola y = 3x2. Its axis of symmetry is x = 0 and its vertex is (0, 0). Since each point on the basic parabola has y = x2 coordinates (a, a2), each point on the parabola y = x2 has coordinates (a, 3a2). Thus the parabola y = 3x2 is obtained from the parabola y = x2 by stretching by a factor of 3 from the x-axis, that is, the y-values are increased by factor of three.
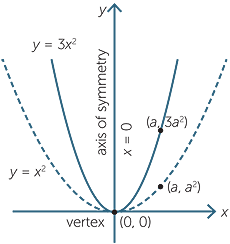
EXERCISE 7
Use transformations to give a quick sketch the following parabolas.
a![]() y = 3x2 + 2
y = 3x2 + 2 ![]() b
b![]() y = 9(x − 1)2
y = 9(x − 1)2![]() c
c![]() y = 3(x − 1)2
y = 3(x − 1)2![]() d
d![]() y = −3x2 + 2
y = −3x2 + 2
Completing the square for non-monic quadratics
The following material should be regarded as extension, since it is tricky and the use of calculus in the senior syllabus can also be used to find the vertex.
The basic method is similar to that used when the coefficient of is x2 is −1. This is demonstrated in the following example.
EXAMPLE
Find the y-intercept, the axis of symmetry and the vertex of the parabolas by completing the square. Sketch their graphs.
a![]() y = 2x2 + 4x + 9
y = 2x2 + 4x + 9 ![]() b
b![]() y = 3x2 + 6x − 13
y = 3x2 + 6x − 13 ![]() c
c![]() y = −2x2 − x + 21
y = −2x2 − x + 21
Solution
| a | Consider the equation y = 2x2 + 4x +9. | ||
| When x = 0, y = 9, so the y-intercept is 9. | |||
| y |
= 2 |
||
= 2 − 1 − 1 |
|||
= 2 |
|||
| = 2(x + 1) 2 + 7 | |||
The axis of symmetry is x = −1 and the vertex is (−1, 7).
Note: This parabola has no x-intercepts since y ≥ 7 for all x.
The axis of symmetry formula
The axis of symmetry is a useful line to find since it gives the x-coordinate of the vertex. We can complete the square on the general quadratic y = ax2 + bx + c and thereby obtain a general formula for the axis of symmetry and hence the x-coordinate for the vertex.
| y | = ax2 + bx + c = a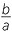 x + x +  |
|
| y | = a 2 + 2 +  − −  |
|
= a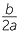  . . |
This expression shows that the minimum (or maximum in the case when is negative) occurs when the first bracket is zero, that is, when x = − .
.
This gives us the equation of the axis of symmetry and also the x-coordinate and the y-coordinate of the vertex.
In practice, students should know and use the formula x = − to find the x-coordinate of the vertex (and equation of the axis of symmetry) and then substitute back to find the y-coordinate.
to find the x-coordinate of the vertex (and equation of the axis of symmetry) and then substitute back to find the y-coordinate.
EXAMPLE
Sketch y = 2x2 + 8x + 19 using the formula for the axis of symmetry.
Solution
When x = 0, y = 19. 
The y-intercept is 19.
The axis of symmetry is
x = − = −
= − = −2.
= −2.
To find the vertex, we calculate the
y-value when x= −2, which is
y = 8 − 16 + 19 = 11.
That is, the vertex is (−2, 11).
Thus the graph has no x-intercepts.
EXERCISE 8
A parabola has vertex (2, −4) and passes through the point (1, 7). Find its equation.
We have seen that the parabola has an axis of symmetry. In the case when the parabola cuts the x-axis, the x-coordinate of the axis of symmetry lies midway between the two x-intercepts. Hence the x-coordinate of the vertex is the average of the x-intercepts. We can use this property in some instances to sketch the parabola.
EXAMPLE
Factor if necessary, and sketch, marking intercepts, axis of symmetry and vertex.
a![]() y = (x − 6)(x − 4)
y = (x − 6)(x − 4)![]() b
b![]() y = 6 + x − x2
y = 6 + x − x2![]() c
c![]() y = 5x2 − 20x + 15
y = 5x2 − 20x + 15
Solution
- a
- y = (x − 6)(x − 4)

When x = 0, y = 24,
so the y-intercept is 24.
When y = 0, x = 4 or x = 6,
so the x-intercepts are 4 and 6.
Taking the average of the x-intercepts,
x = 5 is the axis of symmetry.
When x = 5, y = (5 − 6)(5 − 4) = −1,
so the vertex is (5, −1).
- b
- y = − x2 + x + 6

This is an upside-down parabola.
When x = 0, y = 6, so this is the y-intercept.
| y | = − x2 + x + 6 | |
| = −(x2 − x − 6) | ||
| = −(x − 3)(x + 2) |
- So the x-intercepts are 3 and −2.
Taking their average, the axis of symmetry is x = .
.
When x = , y = −
, y = − +
+  + 6 = 6
+ 6 = 6 so the vertex is
so the vertex is  , 6
, 6 .
.
- c
- y = 5x2 − 20x + 15

When x = 0 then y = 15.
| y | = 5 x2 − 20 x + 15 | |
| = 5 (x2 − 4x + 3 ) | ||
| = 5 (x − 3)( x − 1) |
- So the two x-intercepts are x = 1 and x = 3.
Hence, the axis of symmetry is x = 2 and the vertex is (2, −5).
EXERCISE 9
- a
- Show that there are infinitely many parabolas with x-intercepts 1 and 7.
- b
- What can you say about the axis of symmetry of each of the these parabolas?
- c
- Find the equation of the parabola with x-intercepts 1 and 7 and y-intercept 21.
We have emphasized completing the square because it is a such a useful technique and quickly reveals most of the important features of the parabola. If we are given a parabola in factored form, then we can sketch it without expanding and completing the square.
EXAMPLE
Sketch y = (x − 3)(x − 2) = x2 − 5x + 6.
Solution
Firstly find the intercepts.
- when x = 0, y = 6.
- when y = 0, (x − 3)(x − 2) = 0, so x = 3 or x = 2.
The x-coordinate of the vertex is the average of the x-intercepts, 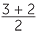 =
=  .
.
To find the y-coordinate of the vertex, we substitute x =  into the equation of the parabola to give,
into the equation of the parabola to give,
y = ![]()

![]() 2 − 5 ×
2 − 5 ×  + 6 = −
+ 6 = − .
.
So the vertex is at ![]()
 , −
, −
![]() .
.
Applications involving quadratics
Quadratics arise in many applications of mathematics.
For example, in physics, the displacement of a particle at time with initial velocity
and acceleration is given by
s = ut +  at2.
at2.
Thus, given the values of u and a, the graph of s against t is a parabola.
EXAMPLE
A cricket ball thrown vertically upwards with initial velocity 30m/s is at a height s at time t given by s = 30t − 5t2. (The acceleration due to gravity is approximately 10m/sec2). What is the maximum height that the ball will reach?
Solution

The axis of symmetry is t = −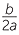 =
= 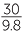 ≈ 3.06. This is the time at which the ball reaches its maximum height. Hence the height at this time is s = 30 − 4.9 ×
≈ 3.06. This is the time at which the ball reaches its maximum height. Hence the height at this time is s = 30 − 4.9 × ![]()

![]() 2 ≈ 45.92 metres.
2 ≈ 45.92 metres.
EXERCISE 10
Referring to the example above, when does the ball return to the ground?
The example above is one of a host of problems where we try to find the value of one variable that will minimise or maximise another. In senior mathematics a more powerful technique using differential calculus will be used to achieve this.
EXAMPLE
A farmer needs to construct a small rectangular paddock using a long wall for one side of the paddock. He has enough posts and wire to erect 200m of fence. What are the dimensions of the paddock if the fences are to enclose the largest possible area?
Solution
Let x m be the length of the side perpendicular to the wall. Then the length of the side parallel to the wall is (200 − 2x)m.
Let A m2 be the area of the paddock.

| Then A | = x(200 − 2x) |
| = 200x − 2x2 |
Hence A = 0 when x = 0 or x = 100 (as in the sketch above). Taking the average, the axis of symmetry is x = 50 and the maximum area occurs when x = 50.
Thus the dimensions of the paddock are 50m by 100m, and the area is 5000 square metres.
EXERCISE 11
A rectangle is constructed so that one vertex is at the origin, another on the graph of the line segment y = 3 −  , where x and y are positive, and the adjacent sides are on the axes. What is the maximum possible area of the rectangle? What are the coordinates of the vertices of such a rectangle?
, where x and y are positive, and the adjacent sides are on the axes. What is the maximum possible area of the rectangle? What are the coordinates of the vertices of such a rectangle?
In earlier modules, we have seen how to solve linear inequalities such as 5x − 2 < 13.
We can also ask the question: For what values of x does the quadratic expression
x2 − 5x − 6 take negative values/positive values.
For example,
- when x = 0, x2 − 5x − 6 = −6 which is negative
- when x = 7, x2 − 5x − 6 = 8 which is positive.
We may then wish to solve the inequalities x2 − 5x − 6 > 0 or x2 − 5x − 6 < 0.
There is a nice graphical approach to solving this problem. To solve the inequality
x2 − 5x + 4 > 0 we draw the graph of the parabola y = x2 − 5x + 4 and see where the values are positive.
The parabola y = x2 − 5x + 4 factors as y = (x − 1)(x − 4) and so the x-intercepts are
x = 1, x = 4. Thus we can draw the graph as shown.
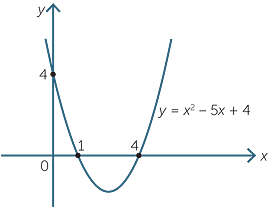
We can see from the diagram that the y-values are positive when x > 4 or when x < 1.
Hence the solution of x2 − 5x + 4 > 0 is x > 4 or x < 1.
Similarly, the solution of x2 − 5x + 4 < 0 is 1 < x < 4.
EXAMPLE
Find the values of x for which 8 − x − x2 < 2.
Solution
8 − x − x2 < 2
x2 + x − 8 > −2 (Multiplying by −1 reverses the inequality.)
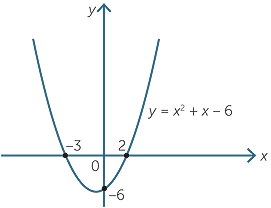 x2 + x − 6 > 0
x2 + x − 6 > 0
Hence we consider the graph
of the parabola y = x2 + x − 6 .
y = (x + 3)(x − 2)
So the solution to the problem
is x < −3 or x > 2.
Quadratics are sometimes called equations of degree 2. Equations of general degree are called polynomials and are covered in detail in the module Polynomials. In general the graph of a polynomial does not share the special symmetry property of a parabola, but many of the other questions such as ‘What are the x-intercepts, what are the y-intercepts?’ are still meaningful.
By expanding out (x − α)(x − β) = 0, we can see that the roots α, β of the quadratic equation x2 + bx + c = 0 satisfy the equations α + β = −b , αβ = c.
Using these relations, we can ask questions about various expressions related to the roots, such as: What is the value of α2 + β2?
From the identity α2 + β2 = (α + β)2 −2αβ and the equations above, we can see that
![]() α2 + β2 = (α + β)2 −2αβ = (−b)2 − 2c = b2 − 2c.
α2 + β2 = (α + β)2 −2αβ = (−b)2 − 2c = b2 − 2c.
The expression α2 + β2 is an example of a symmetric function, since it remains that same if we interchange the two roots.
EXAMPLE
If the roots of the quadratic x2 + 3x + 6 = 0 are α and β, without solving the equation,
find α2 + β2.
Solution
α + β = −3, αβ = 6, so
α2 + β2 = (α + β)2 − 2αβ = (−3)2 − 2 × 6 = −3.
EXERCISE 12
If are the roots of the quadratic equation x2 + bx + c = 0, show that (α − β)2 = b2 − 4c.
(Note that this is equal to the discriminant of the quadratic, so that if the roots are equal, the discriminant is 0. This idea enables us to define the discriminant of a cubic x3 + px + q = 0 or any higher order equation. For example, a cubic with roots α, β, γ is defined to have discriminant (α − β)2(α − γ)2(β − g)2, which can be written in terms p and q of and Thus if the equation has two equal roots, the discriminant will be 0.)
Newton developed the theory of symmetric functions and introduced the so called Newton identities that arise in higher algebra. These apply to the roots of polynomials.
While the quadratic equation and the parabola were known from the days of the Greeks, higher order curves were not studied in depth until the calculus was developed. The basic cubic has equation y = x3 and its graph is shown below.
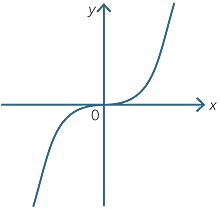
The cubic curve with equation y = x3 − 7x + 6 = (x − 1)(x − 2)(x + 3) has x-intercepts 1, 2,−3 and y-intercept 6. Its graph is shown below.

You will see that there are two turning points on the curve, one somewhere between −3 and 0 and one somewhere between 1 and 2. Unlike the parabola, whose symmetry ensured that the x-coordinate of the turning point was the average of the x-intercepts,
we need calculus to find the x-coordinates of the turning points and they turn out to be
at x = 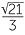 and x = −
and x = − .
.
Focus-directrix definition of a parabola
The parabola has so far been defined as the graph of the function y = ax2 + bx + c.
There is also a geometric definition of the parabola in terms of the path traced out by a moving point. (Such a graph is known as a locus).
Suppose a is a positive real number. Take the point S(0, a) in the plane and draw the line d with equation y = −a. Now find all the points in the plane whose distance from S is equal to its perpendicular distance from the line d. Clearly the origin is one of those points. If we call a typical point with this property (x, y) then we can show, using the distance formula and formula for the perpendicular distance of point to a line, that the equation satisfied by the general point is x2 = 4ay, or y =  . The point S is called the focus of the parabola and the line d is called the directrix. The real number a is called the focal length of the parabola. The physical applications of this are discussed in the following section.
. The point S is called the focus of the parabola and the line d is called the directrix. The real number a is called the focal length of the parabola. The physical applications of this are discussed in the following section.
EXERCISE 13
Use the distance formula to show that the equation satisfied by the point (x, y) in the plane whose distance from the focus S(0, a) is equal to its perpendicular distance from the line
y = −a, is given by x2 = 4ay.
Some of the history of quadratic equations was covered in the module Quadratic Equations. The Parabola originated in Greek geometry from the dissection of a right-cone. Other curves such as the ellipse, the circle and the hyperbola are obtained by intersecting the cone with other planes. These are shown in the following diagram.

The geometric properties of the parabola were studied in some detail by Apollonius of Perga (262−190 BC) in his work on Conics.
We mentioned above that the parabola can also be viewed as the path traced out by a point moving so that its distance from a fixed point, the focus, is equal to its distance from a fixed line called the directrix. This was done by the last of the Greek mathematicians Pappus (290−350 AD).
The parabola, viewed in this way, has the remarkable reflection property that a beam of light (or radio wave) coming into the parabola along a line parallel to the axis of symmetry will reflect off the parabola and pass through the focus. This enables radio waves, light etc to be collected at one point. Conversely, a light source or radio wave emanating from the focus and reflecting off the parabola will move in a direction parallel to the axis of symmetry of the parabola. This property has made the parabola the standard shape used for satellite dishes, reflecting telescopes as well as spotlights and car headlights.

Parabolic reflector. All rays entering parallel to the axis reflect to the focus.
Analysis of the parabola was done geometrically until Descartes (1596−1650) introduced the remarkably simple, yet very powerful, idea of coordinates. The parabola was then studied algebraically as well as geometrically. Armed with these new tools great minds such as Newton and Leibniz were able to develop the calculus and the parabola and higher degree curves were able to be studied in a new way.
Carlyle found an interesting way to solve a quadratic equation graphically using circles and lines. The following exercise exhibits the method.
EXERCISE 14
To solve x2 − gx + h = 0 graphically, let A be the point (0, 1) and B be the point (g, h). Draw a circle with AB as diameter. Then the points (if any) where the circle cuts the x-axis are the roots of the quadratic equation.
- a
- Illustrate the method by solving x2 − 5x + 6 = 0 graphically.
- b
- Prove that the method works.
EXERCISE 1
| a | y = (x + 3)2 | b |  |
EXERCISE 2
- a
- A translation of 2 units to the left and 4 down.
- b
- b vertex: (−2, −4); Axis of symmetry: x = −2
| c |  |
Exercise 3
- a
- If x = 0 then y = 0.
Hence the y-intercept is 0.
| y | = x2 + 4x | ||
| = (x2 + 4x + 4) − 4 | (Add and subtract the square of half the coefficient of x.) |
||
| = (x + 2) 2 − 4 |
- The axis of symmetry is x = −2 and the
vertex is (−2, −4), as in the diagram opposite.
When y = 0, x2 + 4 x = 0
So x(x + 4) = 0
x = 0 or x = −4
The x-intercepts are 0 and −4.
- b
- If x = 0 then y = 0.

Hence the y-intercept is 0.
| Also, y | = x2 − 6x | |
| = (x2 + 6x + 9) − 9 | ||
| = (x − 3)2 − 9 |
- The axis of symmetry is x = 3
and the vertex is (3, -9).
When y = 0, x2 − 6x = 0
So x(x − 6) = 0
x = 0 or x = 6
The x-intercepts are 0 and 6.
- c
- If x = 0 then y = 1.

Thus the y-intercept is 1.
| Also, y | = x2 + x + 1 | |
=   + 1 − + 1 −  |
||
=   2 + 2 +  |
-
The axis of symmetry is x = −
 and
and
the vertex is −
− ,
, 
This graph has no x-intercepts since the
minimum value of y is which is positive.
which is positive.
Exercise 4
- a
- y = x2 + 6x − 7
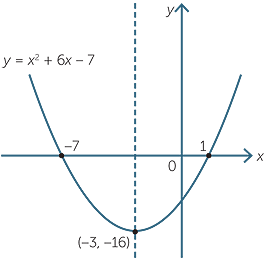
When x = 0, y = −7.
The y-intercept is −7.
| y | = x2 + 6x − 7 | |
| = (x2 + 6x + 9) − 9 − 7 | ||
| = (x + 3)2 − 16 |
the axis of symmetry is x = −3.
Put y = 0, then (x + 3)2 − 16 = 0
(x + 3)2 =16
x + 3= 4 or x + 3 = -4
x = 1 or x = −7
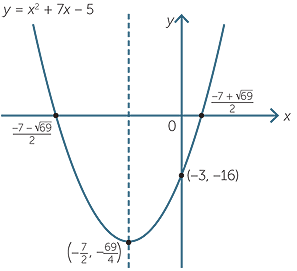
When x = 0, y = −5.
The y-intercept is −5.
| y | = x 2 + 7x − 5 | |
=  x2 + 7x + x2 + 7x + 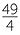  − −  − 5 − 5 |
||
=  x + x +   2 − 2 −  |
-
The vertex is at
 −
− , −
, −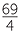
 and the
and the
axis of symmetry is x = − .
.
Put y = 0, then x +
x + 
 2 −
2 −  = 0
= 0
 x +
x + 
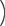 2 =
2 = 
x + =
= 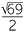 or x +
or x +  = −
= −
x = − +
+ 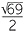 or x = −
or x = − −
− 
x = or x =
or x = 
Exercise 5
- a
- y = −x 2 − 8

The graph y = −x2 − 8 is obtained from
the graph y = −x2 translating 8 units down.
The axis of symmetry is x = 0 and the
vertex is (0, −8). The graph has no x-intercepts. - b
- y = −(x + 3) 2 − 4

| When x = 0, y | = −9 − 4 | |
| = −13 | ||
| The y-intercept is −13. | ||
- The graph y = −(x + 3) 2 − 4 is obtained from the graph y = −x2 by translating 3 units to the left and 4 down. The axis of symmetry is x = −3 and the vertex is (−3, −4). The graph has no x-intercepts.
- c
- y = −(x − 2) 2 + 6

| When x = 0, y | = − (0 − 2) 2 + 6 | |
| = −4 + 6 | ||
| = 2 | ||
| The y-intercept is 2. | ||
The graph y = −(x − 2)2 + 6 is obtained from
the graph y = −x2 by translating 2 units to the
right and 6 up. The axis of symmetry is x = 2
and the vertex is (2, 6). The graph has two x-intercepts.
Exercise 6
- a
- The parabola is y = −x 2 + 8x + 13.
When x = 0, y = 13, so the y-intercept is 13.
Completing the square:
| y | = −[x 2 − 8 x − 13] | ||
| = −[(x2 − 8x − 16) − 13 − 16] | (Complete the square inside the brackets.) | ||
| = −[(x − 4) 2 − 29] | |||
| = −(x − 4) 2 + 29 |
- So the axis of symmetry is x = 4, and the vertex is (4, 29).
When y = 0,
| −(x − 4) 2 + 29 | = 0 | |
| (x − 4)2 | = 29 | |
| x − 4 | = |
- so x = 4 +
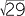 which is positive
which is positive
or x = 4 −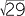 which is negative.
which is negative.
Thus the x-intercepts are 4 +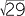 and 4 −
and 4 − 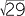 .
.
- b
- Consider the equation y = −x 2 − 3x − 5.
When x = 0, y = −5, so the y-intercept is −5.
Completing the square:
| y | = −[x 2 + 3 x + 5] | |
= − x 2 +3x + x 2 +3x +   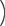 2 2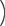 + 5 − + 5 −   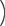 2 2 |
||
= − x + x +  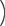 2 + 2 +  |
||
= − x + x +  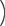 2 − 2 −  |
- So the axis of symmetry is x =
 , and the vertex is
, and the vertex is  −
− , −
, −
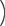 .
.
Note that there are no x-intercepts, since y ≤ − for all x.
for all x.
- c
- Consider the equation y = −x2 − 10x.
When x = 0, y = 0, so the y-intercept is 0.
Completing the square:
| y | = −x2 − 10x | |
| = −[x2 + 10x] | ||
| = −[(x2 + 10x + 25) − 25] | ||
| = −(x + 5)2 − 25 | ||
| = −(x + 5)2 + 25 |
-
Hence the axis of symmetry is x = −5, and the vertex is (−5, 25).
When y = 0,
| −(x + 5)2 + 25 | = 0 | |||||||
| (x + 5)2 | = 25 | |||||||
| x + 5 | = 5 | or | x + 5 | = −5 | ||||
| so | x | = 0 | or | x | = −10 | |||
-
Thus the x-intercepts are x = 0 and x = −10.
EXERCISE 7
| a |  |
b |  |
|||
| c |  |
d |  |
EXERCISE 8
y = 11(x − 2)2 − 4
EXERCISE 9
- a
- The parabolas y = k(x − 1)(x − 7) all have x-intercepts 1 and 7.
- b
- The equation of the axis of symmetry is x = 4.
- c
- y = 3(x − 1)(x − 7)
EXERCISE 10
6 seconds
EXERCISE 11
Maximum area: 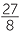 . Coordinates: (0, 0),
. Coordinates: (0, 0), 
 , 0
, 0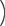 ,
, 
 ,
, 
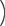 ,
,  0,
0, 
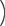
EXERCISE 12
x2 + bx + c = (x − a)(x − b) = x2 − 2(a + b)x + ab
Therefore b = a + b and c = ab
EXERCISE 13
x2 + (y − a)2 = (y + a)2
x2 + y2 − 2ay + a2 = y2 + 2ay + a2
x2 = 4ay
EXERCISE 14
- a
- x = 3 or x = 2
- b
- circle has centre
 ,
, 
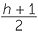
 and radius2 =
and radius2 =  ((g2 + (h − 1)2)
((g2 + (h − 1)2)
Equation of the circle is
 x −
x − 
 2 +
2 +  y −
y − 
 2 = g2 + (h − 1)2
2 = g2 + (h − 1)2
When y = 0,
x2 − gx + +
+  (h2 + 2h + 1) =
(h2 + 2h + 1) =  (g2 + h2 − 2h + 1)
(g2 + h2 − 2h + 1)
x2 − gx + h = 0
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

