The Improving Mathematics Education in Schools (TIMES) Project
- Familiarity with measurement of lengths, angles and area.
- Basic knowledge of congruence and similarity.
- Familiarity with simple geometric proofs.
- Simple geometric constructions.
- Factorisation of whole numbers.
- Simple surd notation.
Is there a simple relationship between the length of the sides of a triangle? Apart from the fact that the sum of any two sides is greater than the third, there is, in general, no simple relationship between the three sides of a triangle.
Among the set of all triangles, there is a special class, known as right-angled triangles or right triangles that contain a right angle. The longest side in a right-angled triangle is called the hypotenuse. The word is connected with a Greek word meaning to stretch because the ancient Egyptians discovered that if you take a piece of rope, mark off 3 units, then 4 units and then 5 units, this can be stretched to form a triangle that contains a right angle. This was very useful to the Egyptian builders.
This raises all sorts of questions. What is so special about the lengths 3, 4 and 5? Are there other sets of numbers with this property? Is there a simple relationship between the lengths of the sides in a right-angled triangle? Given the lengths of the sides of a triangle, can we tell whether or not the triangle is right angled?
Most adults remember the mathematical formula
c2 = a2 + b2
or perhaps
“the square on the hypotenuse is the sum of the squares on the other two sides.”
The first version uses an implied standard notation, the second version uses archaic language but both are Pythagoras’ theorem. This theorem enables us to answer the questions raised in the previous paragraph.
The discovery of Pythagoras’ theorem led the Greeks to prove the existence of numbers that could not be expressed as rational numbers. For example, taking the two shorter sides of a right triangle to be 1 and 1, we are led to a hypotenuse of length ![]() , which is not a rational number. This caused the Greeks no end of trouble and led eventually to the discovery of the real number system. This will be discussed briefly in this module but will be developed further in a later module,The Real Numbers.
, which is not a rational number. This caused the Greeks no end of trouble and led eventually to the discovery of the real number system. This will be discussed briefly in this module but will be developed further in a later module,The Real Numbers.
Triples of integers such as (3, 4, 5) and (5, 12, 13) which occur as the side lengths of right-angled triangles are of great interest in both geometry and number theory − they are called Pythagorean triples. We find all of them in this module.
Pythagoras’ theorem is used in determining the distance between two points in both
two and three dimensional space. How this is done is outlined in the Links Forward section of this module.
Pythagoras’ theorem can be generalised to the cosine rule and used to establish Heron’s formula for the area of a triangle. Both of these are discussed in the Links Forward section.
Let ABC be a triangle. We may write  ABC.
ABC. 
Then by convention, a is length of the interval BC.
We also talk about angle A or ![]() A for
A for ![]() BAC.
BAC.
So a is the length of the side opposite angle A.
Using this notation we can succinctly state Pythagoras’ theorem and two of the most important theorems in trigonometry, the sine rule and the cosine rule. The sine rule and cosine rule are established in the Links Forward section.
 Among the set of all triangles there is a special class known as right-angled triangles or right triangles. A right triangle has one angle, a right angle. The side opposite the right angle is called the hypotenuse. It is the longest side of the triangle
Among the set of all triangles there is a special class known as right-angled triangles or right triangles. A right triangle has one angle, a right angle. The side opposite the right angle is called the hypotenuse. It is the longest side of the triangle
We also talk about the shorter sides of a right-angled triangle.
 Let us use the standard notation described
Let us use the standard notation described
above and assume C = 90°.
If a and b are fixed then c is determined.
Also a < c, b < c and c < a + b.
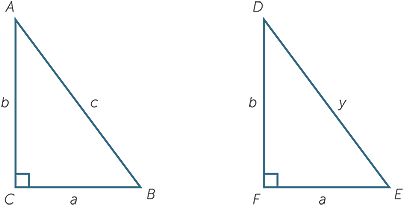 To prove c is determined note that
To prove c is determined note that
 ACB
ACB 
 DFE (SAS), so c = y
DFE (SAS), so c = y
(See the module, Congruence)
A triangle with sides 3 cm, 4 cm, 5 cm is a right-angled triangle. Similarly, if we draw a right-angled triangle with shorter sides 5 cm, 12 cm and measure the third side, we find that the hypotenuse has length ‘close to’ 13 cm. To understand the key idea behind Pythagoras’ theorem, we need to look at the squares of these numbers.
You can see that in a 3, 4, 5 triangle, 9 + 16 = 25 or 32 + 42 = 52 and in the 5, 12, 13 triangle,
25 + 144 = 169 or 52 + 122 = 132.
We state Pythagoras’ theorem:
- The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares
of the lengths of the other two sides. - In symbols c2 = a2 + b2.
EXAMPLE
 Find the length of the hypotenuse in the right triangle opposite.
Find the length of the hypotenuse in the right triangle opposite.
Solution
Let x be the length of the hypotenuse. Then by Pythagoras’ theorem,
x2 = 122+ 162 = 400. So x = 20.
Proof of the theorem
A mathematical theorem is a logical statement, ‘If p then q’ where p and q are clauses involving mathematical ideas. The converse of ‘If p then q’ is the statement, ‘If q then p’.
The converse may or may not be true but certainty needs a separate proof.
Converse of Pythagoras’ theorem: If c2 = a2 + b2 then ![]() C is a right angle.
C is a right angle.
There are many proofs of Pythagoras’ theorem.
Proof 1 of Pythagoras’ theorem
For ease of presentation let  =
=  ab be the area of the right-angled triangle
ab be the area of the right-angled triangle  ABC with right angle at C.
ABC with right angle at C.
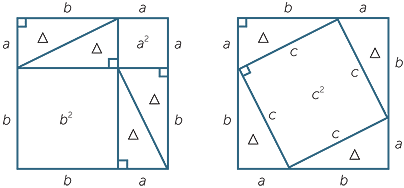 The two diagrams show a square of side length a + b divided up into various squares and triangles congruent
The two diagrams show a square of side length a + b divided up into various squares and triangles congruent
to  ABC.
ABC.
From the left hand diagram
(a + b)2 = a2 + b2 + 4
![]() (1)
(1)
From the right hand diagram
(a + b)2 = 4 + c2
+ c2 ![]()
![]() (2)
(2)
Comparing the two equations we obtain c2 = a2 + b2 and the theorem is proved.
Several other proofs of Pythagoras’ theorem are given in the Appendix.
EXERCISE 1
Find the hypotenuse of the right angled triangles whose other sides are:
a ![]() 5, 12
5, 12 ![]() b
b ![]() 9, 12
9, 12 ![]() c
c ![]() 35, 12
35, 12
d ![]() 15, 8
15, 8 ![]() e
e ![]() 15, 20
15, 20 ![]() f
f ![]() 15, 112
15, 112
Note: Clearly one can use a calculator and reduce each of the above calculations to half a dozen keystrokes. This leads to no insights at all. As a suggestion, if a perfect square is between 4900 and 6400 then the number is between 70 and 80. If the last digit of the square is 1 then the number ends in a 1 or a 9, etc.
Applications of Pythagoras’ theorem
EXAMPLE
 A rectangle has length 8 cm and diagonal 17 cm.
A rectangle has length 8 cm and diagonal 17 cm.
What is its width?
Solution
Let b be the width, measured in cm. Then
| 172 | = 82 + b2 | (Pythagoras’ theorem) | ||
| 289 | = 64 + b2 | |||
| b2 | = 289 − 64 | |||
| = 225, | ||||
| so b = 15. |
The width of the rectangle is 15 cm.
EXERCISE 2
 A ladder of length 410 cm is leaning against a wall. It touches the wall 400 cm above the ground.
A ladder of length 410 cm is leaning against a wall. It touches the wall 400 cm above the ground.
What is the distance between the foot of the ladder and the wall?
The Converse theorem
We now come to the question:
Given the lengths of the sides of a triangle, can we tell whether or not the
triangle is right angled?
This is answered using the converse of Pythagoras’ theorem.
The converse theorem says:
![]() If a2 + b2 = c2 then the triangle is right angled (with right angle at C).
If a2 + b2 = c2 then the triangle is right angled (with right angle at C).
Thus, for example, a triangle with sides 20, 21, 29 is right angled since
| 202 + 212 | = 400 + 441 | |
| = 841 | ||
| = 292 |
The obvious question, which we shall answer later in this module, is can we find all such ‘Pythagorean triples of whole numbers’?
We shall give two proofs of the converse − rather different in nature. However, both use the theorem itself in the proof! This does not often happen in elementary mathematics but is quite common in more advanced topics.
First proof of the converse
 We assume c2 = a2 + b2
We assume c2 = a2 + b2
Construct a second triangle DEF
with ![]() EFD = 90°, EF = a
EFD = 90°, EF = a
and DF = b.
Then, by Pythagoras’ theorem,
ED2 = a2 + b2.
But c2 = a2 + b2 so ED = c. Hence
![]()
 ABC
ABC 
 DEF (SSS).
DEF (SSS).
So, ![]() BCA = 90° since
BCA = 90° since ![]() EFD = 90° and the converse is proved.
EFD = 90° and the converse is proved.
Second proof of the converse
 We assume c2 = a2 + b2
We assume c2 = a2 + b2
Drop the perpendicular from B to AC,
assume D is between A and C.
Clearly x < a and y < b so
| c2 | = x2 + y2 | (Pythagoras’ theorem) | |
| < a2 + b2 = c2 |
This is a contradiction, so C = D or D is to the left of C on the line AC.
EXERCISE 3
Work out the details of the proof when D is to the left of C on the line AC.
EXAMPLE
Which of the triangles below are right-angled triangles?
Name the right angle in each case.
| a | 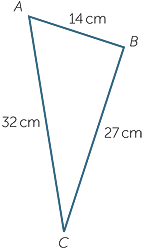 |
b |  |
Solution
a![]() Triangle ABC is not a right-angled triangle since 142 + 272 ≠ 322.
Triangle ABC is not a right-angled triangle since 142 + 272 ≠ 322.
b![]() Triangle DEF is a right-angled triangle since 152 + 362 = 392.
Triangle DEF is a right-angled triangle since 152 + 362 = 392. ![]() F is the right angle
F is the right angle
Consider the sequence ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…
,…

This sequence of positive real numbers is strictly increasing and ![]() is a whole number if and only if n is a perfect square such as 36 or 49. The sequence tends to infinity, that is, there is no upper bound for
is a whole number if and only if n is a perfect square such as 36 or 49. The sequence tends to infinity, that is, there is no upper bound for ![]() .
.
A right-angled triangle with equal side lengths is an isosceles triangle. Hence the angles are 45°, 45° and 90°. If the length of a side is 1 then the hypotenuse is of length ![]() (since 12 + 12 = 2).
(since 12 + 12 = 2).
Next we consider the right-angled triangle with shorter sides 1 and ![]() . It’s hypotenuse has length
. It’s hypotenuse has length ![]() . We can iterate this idea obtaining:
. We can iterate this idea obtaining:

Using the above constructions it follows that a length where n is a whole number greater than 1, can be constructed using just ruler and compass (see module, Constructions).
Since 1 < ![]() < 2,
< 2, ![]() is not a whole number but perhaps
is not a whole number but perhaps ![]() is rational. This is not so, as was discovered about 600BC. These ideas are dealt with in more detail in the module, The Real Numbers.
is rational. This is not so, as was discovered about 600BC. These ideas are dealt with in more detail in the module, The Real Numbers.
When irrational numbers occur in problems involving Pythagoras’ theorem, we can either
- leave the answer in symbolic form, for example
 (= 2
(= 2 ) or
) or - approximate the answer using a calculator, for example 2
 ≈ 4.90
≈ 4.90
(to two decimal places).
EXAMPLE
Find the length, correct to 2 decimal places, 
of the missing side in the right triangle opposite.
solution
By Pythagoras’ theorem,
| x2 + | 52 | = 72 | ||
| x2 + | 25 | = 49 | ||
| x2 | = 24 | |||
| x | = |
|||
| = 2 |
||||
| ≈ 4.90 | (correct to two decimal places) |
EXERCISE 4
A cross-country runner runs 3km west, then 2km south and then 8km east. How far is she from her starting point? Give your answer in kilometres and correct to 2 decimal places.
EXERCISE 5
Find the exact length of the long diagonal in a cube of side length 3 cm.
Three whole numbers that are the lengths of the sides of a right-angled triangle are called a Pythagorean Triad or Pythagorean Triple. Thus, {3, 4, 5} is a Pythagorean Triad.
The formula for how to generate such triples was known by about 2000BC. This is “proved” by a clay tablet (Plimpton 322) which contains fifteen different triples including (1679, 2400, 2929) The tablet is dated to 1800 BC. With your calculator check this is a Pythagorean triple. This was obviously not found by chance!
Starting with (3, 4, 5) we can find or construct infinitely many such triples by taking integer multiples:
(3, 4, 5), (6, 8, 10), (9, 12, 15), …..
Consider a triple (a, b, c) of positive whole numbers with a2 + b2 = c2. If a and b have a common factor then it also divides c. So a useful definition is that the Pythagorean triple (a, b, c) is primitive if, HCF (a, b) = HCF (b, c) = HCF (a, c) = 1 that is, the highest common factor of a and b is 1, etc. If we can find all primitive Pythagorean triples then we can find all triples by simply taking whole number multiples of the primitive triples.
There are various families of examples. Consider the identity:
(n + 1)2 − n2 = 2n + 1
So if 2n + 1 is a perfect square then we can construct a primitive triple ( , n, n + 1). In this way, taking 2n + 1 = 9, 25, 49, 81, ….. we obtain triples:
, n, n + 1). In this way, taking 2n + 1 = 9, 25, 49, 81, ….. we obtain triples:
(3, 4, 5); (5, 12, 13); (7, 24, 25); (9, 40, 41),….
It is possible to list all primitive triples. One form of this ‘classification’ is in the following theorem. We shall prove it using some elementary number theory including the use of the fundamental theorem of arithmetic and the use of the HCF. The symbol | is used for ‘divides exactly into’. The result gives a formula for all primitive Pythagorean Triads.
Theorem
If a2 + b2 = c2 and (a, b, c) is a primitive triad then a = p2 − q2, b = 2pq and
c = p2 + q2 where the HCF of p and q is 1 and p and q are not both odd.
Proof
At least one of a, b and c is odd since the triad is primitive.
The square of a whole number is either a multiple of 4 or one more than a multiple
of 4, hence a and b cannot both be odd.
So we may assume a is odd, b is even and c is odd.
c2 = a2 + b2 so b2 = c2 − a2 = (c − a)(c + a)
Let d be the HCF of c − a and c + a, so d|c −a and d|c + a so d|2c and d|2a
But a and c are coprime so d = 1 or 2 but c − a and c + a are even. So d = 2
Hence we have
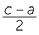 and
and  are coprime integers. But
are coprime integers. But
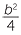 =
= 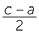 .
.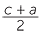 so
so  is a square as is
is a square as is  .
.
Set 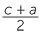 = p2 ,
= p2 , 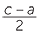 = q2 then c = p2 + q2 , a = p2 − q2 and
= q2 then c = p2 + q2 , a = p2 − q2 and  = p2q2 or b = 2pq.
= p2q2 or b = 2pq.
Finally if p and q are odd then a and c are even which is not the case.
So the theorem is proved.
EXAMPLE
22 − 12 = 3, 2 × 2 × 1 = 4 and 22 + 12 = 5 so the triple (3, 4, 5) corresponds to (p, q) = (2, 1)
EXERCISE 6
Investigate:
a![]() (p, q) = (2, 1), (3, 2), (4, 3), …..
(p, q) = (2, 1), (3, 2), (4, 3), …..
b (p, q) = (4, 1), (5, 2), (6, 3), (7, 4), …..
c (p, q) = (2, 1), (4, 1), (6, 1), (8, 1), …..
EXERCISE 7
Find the values of p and q corresponding to the triple (1679, 2400, 2929) from the clay tablet Plimpton 322. The largest triple on Plimpton 322 is (12 709, 13 500, 18 541) − find p and q in this case as well.
The distance formula in R2 (The coordinate plane)
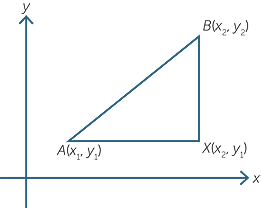 In two dimensional coordinate geometry perhaps the most basic question is ‘What is the distance between two points A and B with coordinates (x1, y1) and (x2, y2)?’
In two dimensional coordinate geometry perhaps the most basic question is ‘What is the distance between two points A and B with coordinates (x1, y1) and (x2, y2)?’
Suppose that A(x1, y1) and B(x2, y2) are two points
in the plane.
Consider the right-angled triangle AXB where
X is the point (x2, y1). Then
| AX | = x2 − x1 or x1 − x2 and | |
| BX | = y2 − y1 or y1 − y2 |
depending on the relative positions of A and B.
By Pythagoras’ theorem
| AB2 | = AX2 + BX2 |
| = (x2 − x1)2 + (y2 − y1)2 |
Therefore AB = BA = 
Distances in three-dimensional space
The distance d from (0, 0) to (x, y) in the coordinate plane satisfies d2 = x2 + y2.
 We can extend coordinate geometry to 3-dimensions by choosing a point O called the origin and choosing three lines through O all perpendicular to each other. We call these lines the x-axis, the y-axis and the z-axis.
We can extend coordinate geometry to 3-dimensions by choosing a point O called the origin and choosing three lines through O all perpendicular to each other. We call these lines the x-axis, the y-axis and the z-axis.
It is possible to go from O to any point P by ‘moving’
a units along the x-axis, then b units parallel to the
y-axis and then c units parallel to the z-axis.
We say the coordinates of the point P are (a, b, c).
Again a basic question is ‘What is the distance OP?’ The answer is
OP2 = a2 + b2 + c2.
To see this, let A = (a, 0, 0) and B = (a, b, 0). The triangle OAB is right-angled at A.
Hence OB2 = OA2 + AB2 = a2 + b2.
Next OBP is right−angled at B so OP2 = OB2 + BP2 = a2 + b2 + c2.
Circles in the plane, centre the origin
A circle is the path traced out by a point moving a fixed distance from a fixed point
called the centre.
First suppose we draw a circle in the Cartesian plane centre the origin and radius 1
and suppose (x, y) is on this circle.

Then by Pythagoras’ theorem (or the distance formula in R2)
x2 + y2 = 12
Conversely, if x2 + y2 = 1 then the point (x, y) lies on the circle of radius 1.
Similarly, if x2 + y2 = r2 then (x, y) lies on the circle, centre the origin, of radius r and conversely all points on this circle satisfy the equation.
Pythagoras’ theorem in trigonometry
 Consider the right-angled triangle ABC, with
Consider the right-angled triangle ABC, with ![]() C = 90° and
C = 90° and ![]() B = θ°
B = θ°
Now by definition cosθ = 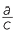 and sinθ =
and sinθ =  .
.
By Pythagoras’ theorem, a2 + b2 = c2. Therefore ![]()
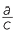
![]() 2 +
2 + ![]()

![]() 2 = 1.
2 = 1.
Hence, one of the most fundamental identities in trigonometry.
cos2 θ + sin2θ = 1
There are 2 important formulas linking the side lengths
of a triangle and the angles of the triangle.
Theorem − The cosine rule
 Let ABC be a triangle with an acute angle at A.
Let ABC be a triangle with an acute angle at A.
Then a2 = b2 + c2 − 2bc cos A
Proof
 Suppose the altitude from C has length h and
Suppose the altitude from C has length h and
divides AB into intervals of length x and y
By Pythagoras’ theorem
![]() b2 = h2 + x2 and
b2 = h2 + x2 and
![]() a2 = h2 + y2
a2 = h2 + y2
Also c = x + y so, eliminating h2
| a2 − b2 | = y2 − x2 | |||
| a2 | = b2 + c2 − (x + y)2 + y2 − x2 | |||
| = b2 + c2 − 2x2 − 2xy | ||||
| = b2 + c2 − 2x(x + y) | ||||
| Now | x | = b cos A and x + y = c |
||
| a2 | = b2 + c2 − 2bc cos A |
EXERCISE 8
Show that the cosine rule is still true when ![]() A is obtuse.
A is obtuse.
Theorem − The sine rule![]()

EXERCISE 9
Write down expressions for sin A and sin B and hence prove the sine rule.

Apollonius’ theorem and Heron’s formula
Euclid’s Elements was written about 300BC. As discussed elsewhere in these modules this amazing set of thirteen books collected together most of the geometry and number theory known at that time. During the next century Apollonius and Archimedes developed mathematics considerably. Apollonius is best remembered for his study of ellipses, parabolas and hyperbolas. Archimedes is often ranked as one of the most important mathematicians of all time. He carried out a number of calculations, which anticipated ideas from integral calculus. In this section we discuss Heron’s formula that scholars believe was discovered by Pythagoras.
We shall prove Apollonius’ theorem and Heron’s formula which both follow from Pythagoras’ theorem using algebra.
Apollonius’ theorem
Suppose  ABC is any triangle, a = 2x and m is the length of the median from A to BC then
ABC is any triangle, a = 2x and m is the length of the median from A to BC then
b2 + c2 = 2x2 + 2m2
Proof
Let length of the altitude AE be h. Also let CE = t, ED = s.

Clearly s + t = x and there are three right-angled triangles so
m2 = h2 + s2
c2 = h2 + (s + x)2
b2 = h2 + t2
Taking into account the formula to be proved we consider
| c2 + b2 − 2m2 | = h2 + (s + x)2 + h2 + t2 − 2h2 −2s2 |
| = s2 + 2sx + x2 + t2 − 2s2 | |
| = x2 + 2sx + t2 − s2 | |
| = x2 + 2sx + (t + s)(t − s) | |
| = x2 + 2sx + (t − s)x | |
| = x2 + sx + tx | |
| = 2x2 | |
| That is, b2 + c2 | = 2m2 + 2x2 |
In the above diagram we asumed then ![]() C is acute and E is between C and B. The other cases can be dealt with similarly.
C is acute and E is between C and B. The other cases can be dealt with similarly.
EXERCISE 10
Use the cosine rule to write m2 in  ACD and c2 in
ACD and c2 in  ACB.
ACB.
Deduce Apollonius’ theorem in a couple of steps.
Heron’s formula
This is an amazing formula expressing the area of a triangle in terms of its side lengths.
To write this in its standard form consider a  ABC with side lengths a, b and c.
ABC with side lengths a, b and c.
We let 2s = a + b + c and let  be the area of
be the area of  ABC (s is the semi-perimeter
ABC (s is the semi-perimeter
of the triangle). Then
![]()
![]()
![]()
![]()
![]()
 2 = s (s − a) (s − b) (s − c)
2 = s (s − a) (s − b) (s − c)
We give a proof that uses only Pythagoras’ theorem, the formula for the area of a triangle and some algebra.
Proof
 Let h be the length of the altitude from C to AB which divides AB into intervals of length x and y.
Let h be the length of the altitude from C to AB which divides AB into intervals of length x and y.
Then x + y = c.
The area of a triangle is half base times height so
 =
=  hc and 4
hc and 4 2 = h2c2 (1)
2 = h2c2 (1)
Pythagoras’ theorem gives
a2 = h2 + x2 (2)
b2 = h2 + y2 = h2 + (c − x)2 (3)
We must eliminate h and x from equations (1), (2) and (3). This is non-trivial!
| (2) − (3) a2 − b2 = h2 + x2 − h2 − (c − x)2 | |
| a2 − b2 = 2cx − c2 | |
| 2cx = a2 + c2 − b2 (4) |
Next (2) gives
| h2 = a2 − x2 |
substitute into (1)
4 2 = c2(a2 − x2) 2 = c2(a2 − x2) |
|
16 2 = 4c2a2 − 4c2x2 (5) 2 = 4c2a2 − 4c2x2 (5) |
Square (4) and substitute into (5)
|
16 |
= (2ca)2 − (a2 + c2 − b2)2 |
This is the difference of two squares, so
|
16 |
= (2ca + a2 + c2 − b2)(2ca − a2 − c2 + b2) |
|
|
= ((a + c)2 − b2)(b2 − (a − c)2) |
||
|
= (a + c + b)(a + c − b)(b + a − c)(b − a + c) |
||
|
= 2s(2s − 2b)(2s − 2c)(2s − 2a) |
| So |  2 = s(s − a)(s − b)(s − c) 2 = s(s − a)(s − b)(s − c) |
EXERCISE 11
Find the areas of the triangles with side lengths:
a ![]() 13, 14, 15
13, 14, 15 ![]() b
b ![]() 13, 20, 21
13, 20, 21 ![]() c
c ![]() 10, 17, 21
10, 17, 21 ![]() d
d ![]() 51, 52, 53
51, 52, 53
As outlined above, the theorem, named after the sixth century BC Greek philosopher and mathematician Pythagoras, is arguably the most important elementary theorem in mathematics, since its consequences and generalisations have wide ranging applications.
It is often difficult to determine via historical sources how long certain facts have been known. However, in the case of Pythagoras’ theorem there is a Babylonian tablet, known as Plimpton 322, that dates from about 1700BC. This tablet lists fifteen Pythagorean triples including (3, 4, 5), (28, 45, 53) and (65, 72, 97). It does not include (5, 12, 13) or (8, 15, 17) but it does include (12 709, 13 500, 18 541)! The fifteen triples correspond (very roughly) to angles between 30° and 45° in the right-angled triangle. The Babylonian number system is base 60 and all of the even sides are of the form 2a 3b 5c presumably to facilitate calculations in base 60. Most historical documents are found as fragments and one could call this the Rosetta Stone of mathematics. Whichever interpretation of the purpose of Plimpton 322 is correct, and there are several, it is clear that both Pythagoras’ theorem and how to construct Pythagorean Triples was known well before 1700BC.
The nature of mathematics began to change about 600 BC. This was closely linked to the rise of the Greek city states. There was constant trade and hence ideas spread freely from the earlier civilisations of Egypt and Babylonia. Most of the history is lost forever, but tradition has it the Thales, Pythagoras and their students, were responsible for developing many of the key ideas − in particular the need to prove theorems! What we do know is what was known at about 300BC. This is because Euclid of Alexandria wrote his thirteen volume book the Elements. Contrary to popular belief, this book is by no means solely about geometry.
Book 1 of the Elements is on geometry and attempts to set geometry on a sound logical basis by giving some twenty-three definitions and lists five postulates and five common notions. This axiomatic approach, although flawed and incomplete gave a logical approach to the study of geometry which was a central part of a classical education right up to the twentieth century. The imperfections of Euclid were not fixed until 1900 when David Hilbert gave a modern correct system of axioms. In Book 1 of Euclid a number of theorems are proved such as the well-known result that in an isosceles triangle the base angles are equal. The final theorem, Proposition 1-47, is Pythagoras’ theorem. The proof given is not the easiest known at the time, but uses only congruence and other results proved in Book 1. Euclid’s Elements are very sophisticated.
Other proofs of Pythagoras’ theorem
There are hundreds of proofs of Pythagoras’ theorem −
one attributed to Napoleon and one attributed to a 19th century US president!
We shall present a few more including Euclid’s proof.
Second proof
 We take the second diagram from the first proof.
We take the second diagram from the first proof.
 is the area of the triangle so
is the area of the triangle so  =
=  ab.
ab.
The large square is a + b by a + b so
(a + b)2 = 4 + c2
+ c2
a2 + 2ab + b2 = 4 ab + c2
ab + c2
or c2 = a2 + b2.
Third proof
 We assume b > a.
We assume b > a.
The side length of the inner square is b − a
Hence
![]() (b − a)2 + 4
(b − a)2 + 4 = c2
= c2
![]() a2 − 2ab + b2 + 2ab = c2
a2 − 2ab + b2 + 2ab = c2
![]() a2 + b2 = c2
a2 + b2 = c2
and we have another proof of Pythagoras’ theorem.
The first three proofs are essentially based on congruence of triangles, partially disguised as sums of areas. Some proofs use similarity. One of the nicest or perhaps minimalist proofs comes from considering, a simple diagram which contains three triangles all similar to each other.
Fourth proof
We take an arbitrary right-angled triangle ABC with ![]() C = 90° and let CD be an altitude of the triangle of length h.
C = 90° and let CD be an altitude of the triangle of length h.
CD is perpendicular to AB and x + y = c 
 ACD is similar to
ACD is similar to  CBD (AAA), hence
CBD (AAA), hence 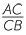 =
=  =
= 
![]()
![]() That is,
That is, 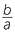 =
= 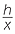 =
= 
 ACD is similar to
ACD is similar to  ABC (AAA), hence
ABC (AAA), hence 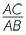 =
= 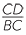 =
= 
![]()
![]() That is,
That is, 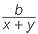 =
= 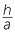 =
= 
 CBD is similar to
CBD is similar to  ABC (AAA), hence
ABC (AAA), hence 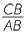 =
= 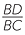 =
= 
![]()
![]() That is,
That is, 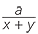 =
= 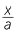 =
= 
From the second group of equations we obtain (by cross multiplication)
![]() b2 = y(x + y)
b2 = y(x + y)
Similarly, from the third group we obtain
![]() a2 = x(x + y)
a2 = x(x + y)
Hence
a2 + b2 |
= x(x + y) + y(x + y) |
|
= (x + y)2 |
||
= c2 |
and the proof is complete.
 Next we shall discover Pythagoras’ proof of his theorem. More properly it is Euclid’s proof − proposition 47 of Euclid’s elements.
Next we shall discover Pythagoras’ proof of his theorem. More properly it is Euclid’s proof − proposition 47 of Euclid’s elements.
We draw squares of areas a2, b2 and c2 adjacent to the sides of the triangle ABC.
| From | b2 = y(x + y) = yc in the previous proof | |
y =  |
||
| From | a2 = x(x + y) = xc in the previous proof | |
x =  |
The area of the shaded rectangle is
cx =  = a2
= a2
and the other rectangle is
cy =  = b2
= b2
So we have divided the square, area c2 , into two rectangles of area a2 and b2. This is the key idea in Euclid’s proof.
Fifth proof: Euclid’s proof
 Euclid’s proof of Pythagoras consists of proving the square of area b2 is the same as the area of a
Euclid’s proof of Pythagoras consists of proving the square of area b2 is the same as the area of a
rectangle. This is done by finding congruent triangles
of half the area of the two regions.
Here are the details:
 EAB is congruent to
EAB is congruent to  CAG (SAS)
CAG (SAS)
since
|
EA |
= AC |
(sides of a square) |
|
|
AB |
= AG |
(sides of a square) |
|
|
|
= |
(equal to 90° + |
Hence area  EAB = area
EAB = area  CAG
CAG
area ACDE = 2 × area  EAB
EAB ![]() (triangle and rectangle on same base and same height)
(triangle and rectangle on same base and same height)
Similarly, area AGHF = 2 × area  CAG so,
CAG so,
area AGFH = area ACDE = b2.
In a similar way it can be shown that area BHFI = a2 and the theorem is proved.
EXERCISE 1
a![]() 13
13 ![]() b
b![]() 15
15 ![]() c
c![]() 37
37 ![]() d
d![]() 17
17 ![]() e
e![]() 25
25 ![]() f
f![]() 113
113
EXERCISE 2
90 cm
EXERCISE 3
Let DC = y where D is the point on AC produced so that BD is perpendicular to AC produced. Let BD = x.
Assume c2 = a2 + b2
Using Pythagoras’ theorem in triangle BDC: a2 = x2 + y2.
Using Pythagoras’ theorem in triangle BDA: c2 = x2 + (y + b)2.
Use the three equations to show 2by = 0 which is a contradiction.
EXERCISE 4
5.39 km
EXERCISE 5
3![]() cm
cm
EXERCISE 6
a
| p | q | a | b | c |
| 2 | 1 | 3 | 4 | 5 |
| 3 | 2 | 5 | 12 | 13 |
| 4 | 3 | 7 | 24 | 25 |
| 5 | 4 | 9 | 40 | 41 |
| 6 | 5 | 11 | 60 | 61 |
| 7 | 6 | 13 | 84 | 85 |
| 8 | 7 | 15 | 112 | 113 |
| 9 | 8 | 17 | 144 | 145 |
| 10 | 9 | 19 | 180 | 181 |
b
| p | q | a | b | c |
| 4 | 1 | 15 | 8 | 17 |
| 5 | 2 | 21 | 20 | 29 |
| 6 | 3 | 27 | 36 | 45 |
| 7 | 4 | 33 | 56 | 65 |
| 8 | 5 | 39 | 80 | 89 |
| 9 | 6 | 45 | 108 | 117 |
| 10 | 7 | 51 | 140 | 149 |
| 11 | 8 | 57 | 176 | 185 |
| 12 | 9 | 63 | 216 | 225 |
| 13 | 10 | 69 | 260 | 269 |
c
| p | q | a | b | c |
| 2 | 1 | 3 | 4 | 5 |
| 4 | 1 | 15 | 8 | 17 |
| 6 | 1 | 35 | 12 | 37 |
| 8 | 1 | 63 | 16 | 65 |
| 10 | 1 | 99 | 20 | 101 |
EXERCISE 7
p = 48 and q = 25 ![]() and p = 125 and q = 54.
and p = 125 and q = 54.
EXERCISE 8
Let D be the point on BA produced so that CD is perpendicular to BA produced.
Let CD = h and DA = x.
Use Pythagoras’ theorem twice:
b2 = h2 + x2 and a2 = h2 + (x + c)2. Eliminate h and substitute x = b cos(180 − A) = −b cos A to obtain the result.
EXERCISE 9
Use h = b sin A = a sin B so 
EXERCISE 10
m2 = b2 + x2 − 2bx cos C and c2 = b2 + 4x2 − 4bx cos C.
Multiply the first equation by 2 and subtract the second equation to obtain the result.
EXERCISE 11
a ![]() 84
84 ![]() b
b ![]() 126
126 ![]() c
c ![]() 84
84 ![]() d
d ![]() 1170
1170
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


