The Improving Mathematics Education in Schools (TIMES) Project
- The content of the modules Quadratic Equations, Quadratic Functions.
- Familiarity with coordinate geometry, and elementary graphs, including the graph
of y = x2.
Polynomials represent the next level of algebraic complexity after quadratics. Indeed a quadratic is a polynomial of degree 2. We can factor quadratic expressions, solve quadratic equations and graph quadratic functions, the obvious question arises as to
how these things might be performed with algebraic expressions of higher degree.
The quadratic x2 − 5x + 6 factors as (x − 2)(x − 3). Hence the equation x2 − 5x + 6 = 0
has solutions x = 2 and x = 3.
Similarly we can factor the cubic x3 − 6x2 + 11x − 6 as (x − 1)(x − 2)(x − 3), which enables us to show that the solutions of x3 − 6x2 + 11x − 6 = 0 are x = 1, x = 2 or x = 3. In this module we will see how to arrive at this factorisation.
Polynomials in many respects behave like whole numbers or the integers. We can add, subtract and multiply two or more polynomials together to obtain another polynomial. Just as we can divide one whole number by another, producing a quotient and remainder, we can divide one polynomial by another and obtain a quotient and remainder, which are also polynomials.
A quadratic equation of the form ax2 + bx + c has either 0, 1 or 2 solutions, depending on whether the discriminant is negative, zero or positive. The number of solutions of the this equation assisted us in drawing the graph of the quadratic function y = ax2 + bx + c. Similarly, information about the roots of a polynomial equation enables us to give a rough sketch of the corresponding polynomial function.
As well as being intrinsically interesting objects, polynomials have important applications in the real world. One such application to error-correcting codes is discussed in the Appendix to this module.
A polynomial is as expression such as x5 − 2x3 + 8x + 3 or  x4 −
x4 − ![]() x2 + 1. There may be any number of terms, but each term must be a multiple of a whole number power of x. Thus 2x3 − x
x2 + 1. There may be any number of terms, but each term must be a multiple of a whole number power of x. Thus 2x3 − x is not a polynomial.
is not a polynomial.
The term with the highest power of is called the leading term and its coefficient is called the leading coefficicent. If the leading coefficient is 1, then the polynomial is called monic. The index of the leading term is called the degree of the polynomial. The term independent of is called the constant term.
Thus x5 − 2x3 + 8x + 3 is a monic polynomial of degree 5 with constant term 3, while  x4 −
x4 − ![]() x2 + 1 is a non-monic polynomials of degree 4 with leading coefficient
x2 + 1 is a non-monic polynomials of degree 4 with leading coefficient  and constant term 1.
and constant term 1.
In the first polynomial, the coefficients are all integer while the second polynomials has an irrational coefficient. For the most part, we will consider only polynomials of the first type, but much of what follows applies equally well to the second.
To name polynomials, we will use the function notation such as p(x) or q(x). Thus we can write p(x) = x5 − 2x3 + 8x + 3, or q(x) =  x4 −
x4 − ![]() x2 + 1. This enables us to conveniently substitute values of x when required.
x2 + 1. This enables us to conveniently substitute values of x when required.
The general polynomial has the form
![]() p(x) = anxn − an − 1xn − 1 + ... + a1x + a0,
p(x) = anxn − an − 1xn − 1 + ... + a1x + a0,
where an ≠ 0 and n is a whole number. The coefficients are, in general, real numbers.
EXERCISE 1
Write down the leading term, the leading coefficient, the degree and the constant term in the general polynomial given above.
For small degree polynomials, we use the following names.
- a polynomial of degree 1 is called linear
- a polynomial of degree 2 is called a quadratic
- a polynomial of degree 3 is called a cubic
- a polynomial of degree 4 is called a quartic
- a polynomial of degree 5 is called a quintic
A polynomial that consists only of a non-zero constant, is called a constant polynomial and has degree 0. The polynomial p(x) = 0 is called the zero polynomial. It has no terms and so there is no leading term. It is best not to define the degree of the zero polynomial. Some books write its degree as −1 or −∞.
Adding, subtracting and multiplying polynomials
To add or subtract two polynomials, we collect the like terms.
EXAMPLE
Let p(x) = 3x4 − 2x2 + x − 1, q(x) = 7x5 + 2x2.
Find ![]() a
a![]() p(x) + q(x)
p(x) + q(x) ![]() b
b![]() p(x) − q(x)
p(x) − q(x) ![]() c
c![]() 2p(x) − 3q(x).
2p(x) − 3q(x).
Solution
a![]() p(x) + q(x) = 7x5 + 3x4 + x − 1
p(x) + q(x) = 7x5 + 3x4 + x − 1
b![]() p(x) − q(x) = −7x5 + 3x4 − 4x2 − 1
p(x) − q(x) = −7x5 + 3x4 − 4x2 − 1
c![]() 2p(x) − 3q(x) = 14x5 − 9x4 + 10x2 − 3x + 3.
2p(x) − 3q(x) = 14x5 − 9x4 + 10x2 − 3x + 3.
Notice that we usually write the terms in the polynomial from largest to smallest degree. This is sometimes called the standard form of the polynomial.
To multiply two polynomials, we multiply each term in the first polynomial by second polynomial and collect like terms.
EXAMPLE
The polynomials P(x), Q(x) and R(x) are given by P(x) = x3 − 2x2 + x − 1, Q(x) = 3x3 − 2x2 and R(x) = −x4 + 2x3 − 3x2. Find:
a![]() P(x)Q(x)
P(x)Q(x) ![]() b
b![]() Q(x)R(x)
Q(x)R(x)
Solution
| a | P(x)Q(x) | = (x3 − x2 + x − 1)(3x3 − 2x2) | |
| = x3(3x2 − 2x2) − x2(3x3 − 2x2) + x(3x3 − 2x2) − (3x3 − 2x2) | |||
| = 3x6 − 2x5 − 3x5 + 2x4 + 3x4 − 2x3 − 3x3 + 2x2 | |||
| = 3x6 − 5x5 + 5x4 − 5x3 + 2x2 | |||
| b | Q(x)R(x) | = (3x3 − 2x2)(−x4 + 2x3 − 3x2) | |
| = 3x3(−x4 + 2x3 − 3x2) − 2x2(−x4 + 2x3 − 3x2) | |||
| = −3x7 + 6x6 − 9x5 + 2x6 − 4x5 + 6x4 | |||
| = −3x7 + 8x6 − 13x5 + 6x4 |
EXERCISE 2
a![]() Square the polynomial p(x) = 2x3 − x + 1.
Square the polynomial p(x) = 2x3 − x + 1.
b![]() Complete the statements:
Complete the statements:
![]() i
i![]() When two non-zero polynomials are multiplied, the degree of the product is .......
When two non-zero polynomials are multiplied, the degree of the product is .......
![]() ii
ii![]() The constant term in the product of two polynomials is ..........
The constant term in the product of two polynomials is ..........
When one whole number is divided into another a quotient and remainder is formed. Thus gives 7 remainder 2. There are various ways to write this result.
- 37 ÷ 5 equals 7 remainder 2
- 37 ÷ 5 = 7
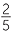
- 37 = 7 × 5 + 2
In the statement 37 ÷ 5 equals 7 remainder 2
- the number 5 that we are dividing by is called the divisor
- the number 37 that we are dividing into is called the dividend
- the number 7 is called the quotient
- the number 2 is called the remainder
The key point about the remainder is that it is non-negative but strictly less than the divisor. Thus, using the third representation, when we divide two whole numbers p and d > 0 we can write
![]() p = dq + r, where 0 ≤ r ≤ d.
p = dq + r, where 0 ≤ r ≤ d.
If the remainder is zero, then we cay that d is a factor of p.
These basic statements regarding arithmetic have analogues when we come to divide one polynomial by another. We will use the same terminology when discussing polynomial division. The process of doing this is modelled on long division.
The division of the polynomial p(x) by the polynomial d(x) also produces a quotient q(x) and a remainder r(x) and so we can write
p(x) = d(x)q(x) + r(x).
The key idea in performing the division is to keep working with the leading terms, as the following example shows.
EXAMPLE
We will divide the polynomial p(x) = 5x4 −7x3 + 2x − 4 by the polynomial d(x) = x − 2, and then express the division in the form p(x) = d(x)q(x) + r(x).
Solution
| 5x3 | + | 3x2 | + | 6x | + | 14 | |||||
| x − 2 | 5x4 | − | 7x3 | + | 2x | − | 4 | (Divide x into 5x4, giving 5x3.) | |||
| 5x4 | − | 10x3 | (Multiply x − 2 by 5x3 and then subtract.) | ||||||||
| 3x3 | + | 2x | − | 4 | (Divide x into 3x3, giving 3x2.) | ||||||
| 3x3 | − | 6x2 | (Multiply x − 2 by 3x2 and then subtract.) | ||||||||
| 6x2 | + | 2x | − | 4 | (Divide x into 6x2, giving 6x.) | ||||||
| 6x2 | − | 12x | (Multiply x − 2 by 6x and then subtract.) | ||||||||
| 14x | − | 4 | (Divide x into 14x, giving 14.) | ||||||||
| 14x | − | 28 | (Multiply x − 2 by 14 and then subtract.) | ||||||||
| 24 | (This is the final remainder.) |
Hence 5x4 − 7x3 + 2x − 4 = (x − 2)(5x3 + 3x2 + 6x + 14) + 24. (1)
In this example, we see that the quotient is q(x) = 5x3 + 3x3 + 6x − 14 and the remainder is r(x) = 24.
We can perform a partial check by substituting x = 2 into the last line.
It can be seen from the above example that the degree of the remainder is less than the degree of the divisor, since otherwise, we could continue the division. Thus, in the case when is a linear factor, the remainder will be a constant and so we can write it as .
In general, we can now write p(x) = d(x)q(x) + r(x), where r(x) = 0, or, 0 ≤ degree (r(x)) < degree (d(x)).
EXERCISE 3
Divide p(x) = 5x4 − 7x3 + 2x − 4 by d(x) = x2 − 2. Express the result in the form
p(x) = d(x)q(x) + r(x) where the degree of r(x) is less than the degree of d(x).
Note that in this case, since the divisor has degree 2, the remainder will either be 0 or have degree at most 1.
The remainder theorem
Long division of polynomials is a cumbersome process and in some instances we are only interested in the remainder. This does not appear until the end of the computation. When we divide a polynomial p(x) by a linear factor (x − a), we can find the remainder quite easily.
Since the divisor is linear, p(x) = (x − a)q(x) + r where r is a constant. Substituting x = a into both sides, we have r = p(a).
Thus the remainder is equal to the polynomial evaluated at x = a.
This surprising result is called the remainder theorem. We should keep in mind that it says nothing at all about the quotient q(x) and only works when we are dividing by a linear factor (x − a).
EXAMPLE
Find the remainder when p(x) = x4 − 3x2 − 10x + 2 is divided by
a![]() (x − 3)
(x − 3)![]() b
b![]() (x + 4)
(x + 4) ![]() c
c![]() (2x − 1)
(2x − 1)
Solution
- a
- The remainder is p(3) = 81 − 27 − 30 + 2 = 26
- b
- Since (x + 4) = (x − (−4)), the remainder is p(−4) = 256 − 48 + 40 + 2 = 250
- c
- Write p(x) = (2x − 1)q(x) + r, so we can obtain r by substituting x =
 in both sides. Hence the remainder is r
in both sides. Hence the remainder is r =
= 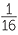 −
−  − 5 + 2 = −
− 5 + 2 = −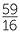 .
.
EXERCISE 4
The polynomial p(x) = x5 − 7x3 + ax + 1 has remainder 13 after division by x − 1. Find the value of the coefficient a.
The factor theorem
Factoring quadratics is an important technique which we used to solve quadratic equations. In a similar way, we would like to be able to develop some techniques to factor polynomials.
If the linear polynomial (x − a) is a factor of a polynomial p(x) then we can write
p(x) = q(x)(x − a) and so the remainder when p(x) is divided by (x − a) is equal to 0.
Using the remainder theorem, we have now proven:
Theorem
(x − a) is a factor of the polynomial p(x) if p(a) = 0. If p(a) ≠ 0, then
(x − a) is not a factor of p(x).
The number a which gives p(a) = 0 is called a zero of the polynomial.
EXAMPLE
Which of the following are factors of p(x) = x3 − 6x2 + 11x − 6?
a![]() (x − 2)
(x − 2) ![]() b
b![]() (x + 1)
(x + 1) ![]() c
c![]() (x − 1).
(x − 1).
Solution
- a
- p(2) = 8 − 24 + 22 − 6 = 0 and so (x − 2) is a factor of p(x).
- b
- p(−1) = − 1 − 6 − 11 − 6 ≠ 0 and so (x + 1) is not a factor of p(x).
- c
- p(1) = 1 − 6 + 11 − 6 = 0 and so (x − 1) is a factor of p(x).
Notice that since (x − 2) and (x − 1) are both factors of p(x) then so is their product
(x − 2)(x − 1) = x2 − 3 x + 2. We could thus find the third factor by long division.
Dividing p(x) by x2 − 3x + 2 gives (x − 3) as the third factor and so we have the
following factorisation,
![]() p(x) = x3 − 6x2 + 11x − 6 = (x − 1)(x − 2)(x − 3).
p(x) = x3 − 6x2 + 11x − 6 = (x − 1)(x − 2)(x − 3).
Alternative method
Since p(2) = 0 and p(1) = 0, and p(x) has degree 3, we can write p(x) = (x − 2)(x − 1) (x − a)
Where a is a number to be determined. Since p(0) = −6 we have −2a = −6, so a = 3.
EXERCISE 5
The polynomial p(x) = 3x6 − 5x3 + ax2 + bx + 10 is divisible by x + 1 and x − 2. Find the values of the coefficients a and b.
Our aim is to take a polynomial with integer coefficients and write it as a product of polynomials of smaller degree which also has integer coefficients. This process is called factoring over the integers.
The factor theorem allows us to check if a polynomial p(x) has a linear factor (x − a). If it does, then we can use long division to find a polynomial q(x) such that p(x) = (x − a)q(x) and q(x) has degree one less than the degree of p(x). Thus we may be able to repeat the process on q(x) and so on as often as possible to give a complete factorisation of p(x).
For example,
We begin with polynomial p(x) = x3 + 4x2 − 7x − 10.
- We search systematically for one linear factor, by checking the numbers a = 1, − 1, 2, −2, … until we find an integer value of a such that p(a) = 0.
p(1) = −12 ≠ 0, p(−1) = 0 so (x + 1) is factor.
- Next we use long division to divide p(x) by (x + 1) to obtain p(x) = (x + 1)(x2 + 3x − 10).
Now the quadratic q(x) = x2 + 3x − 10 can be factored, using our knowledge of quadratics, as (x + 5)(x − 2) and so the complete factorisation of p(x) is
p(x) = (x+1)(x + 5)(x − 2).
To assist us in finding an integer zero of the polynomial we use the following result.
Theorem
If the polynomial
p(x) = anxn + an−1xn−1 + … + a1x + a0
has an integer zero a, then a is a factor of the constant term a0.
Thus, in the example above, the only possible integer zeroes are ±1, ±2, ±5 or ±10.
EXERCISE 6
Explain why the above theorem is true.
EXAMPLE
Factorise the polynomial p(x) = x4 − 2x3 − 8x + 16.
Solution
- We only need to test the positive and negative factors of 16.
P(1) = 1 − 2 − 8 + 16 ≠ 0, so x − 1 is not a factor of p(x).
P(−1) = 1 + 2 + 8 + 16 ≠ 0, so x + 1 is not a factor of p(x).
P(2) = 16 − 16 − 16 + 16 = 0, so x − 2 is a factor.
After long division of p(x) by x − 2, p(x) = (x − 2)(x3 − 8)
- Let Q(x) = x3 − 8.
x − 1 and x + 1 are not factors of Q(x) since P(x) = (x − 2)Q(x), and they are not factors of P(x).
However, Q(2) = 8 − 8 = 0, so x − 2 is a factor of Q(x) as well.
After long division of Q(x) by x − 2, Q(x) = (x − 2) (x2 +2x + 4).
- The quadratic x2 + 2x + 4 cannot be factorised, see below.
Hence P(x) = (x − 2)2(x2 + 2x + 4) is the complete factorisation of P(x).
Note that the quadratic x2 + 2x + 4 = (x + 1) 2 + 3 which is always greater or equal to 3, hence the quadratic has no factors.
EXERCISE 7
By firstly removing the obvious common factor, factorise the polynomial
p(x) = 2x5 − 22x4 + 78x3 − 90x2.
One of the main methods of solving quadratic equations was the method of factoring. Similarly, one of the main applications of factoring polynomials is to solve polynomial equations.
EXAMPLE
Solve x3 + 4 x2 − 7x − 10 = 0
Solution
In an earlier example, we factored the polynomial
p(x) = x3 + 4 x2 − 7x − 10 = 0 as (x + 1)(x + 5)(x − 2).
Thus, the equation x3 + 4 x2 − 7x − 10 = 0 becomes (x + 1)(x + 5)(x − 2) = 0
Since the product of the three factors is zero, we can equate each factor to zero to find the solutions. Thus, x + 1 = 0 or x − 2 = 0 or x + 5 = 0 giving x = −1, x = 2 or x = −5.
Note: The polynomial p(x) = (x − 1)(x − 2) 2(x − 4) 3 is of degree 6, but the polynomial equation (x − 1)(x − 2)2(x − 4) 3 = 0 has only 3 (distinct) solutions x = 1 or x = 2 or x = 4. Thus the number of (distinct) solutions may be less than the degree, but it can never exceed the degree.
EXERCISE 8
Use the factorisation of p(x) = 2x5 − 22x4 + 78x3 −90x2 from the above exercise to solve the equation 2x5 − 22x4 + 78x3 − 90x2 = 0.
In some situations, the factorisation results in a quadratic equation with either no real solutions or irrational solutions. In this case, we may need to complete the problem by using the quadratic formula.
EXAMPLE
Solve x4 + 7x3 − 2x2 − 7x + 1 = 0
Solution
The polynomial x4 + 7x3 − 2x2 − 7x + 1 has factorisation (x − 1)(x + 1)(x2 + 7x − 1).
Hence the equation becomes (x − 1)(x + 1)( x2 + 7x − 1) = 0.
Thus the solutions are x = 1, x = −1 and the solutions to x2 + 7x − 1 = 0.
Using the quadratic formula, b2 − 4ac = 49 + 4 = 53, so the quadratic has solutions
x = 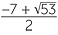 and x =
and x = 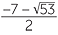 .
.
Hence the quartic has four solutions x = 1, −1, 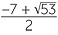 and x =
and x = 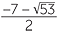 .
.
Note that there are polynomial equations with irrational roots that cannot be solved using the procedure above. For example, the polynomial p(x) = x5 − 3x3 − 2x2 + 6 factors as
(x2 − 3)(x3 − 2) and so the equation x5 − 3x3 − 2x2 + 6 = 0 has solutions, x = ![]() , x = −
, x = −![]() , and x =
, and x = ![]() .
.
In general, factoring polynomials over the integers is a difficult problem. The polynomial
x3 − 2, for example, cannot be factored over the integers, but it does have one real solution, x = ![]() .
.
Sketching polynomial functions
A polynomial function is a function of the form y = p(x), where p(x) is a polynomial.
In the module, Quadratic Functions we saw how to sketch the graph of a quadratic
by locating
- the intercepts
- finding the vertex.
The vertex is an example of a turning point.
For polynomials of degree greater than 2, finding turning points is not an elementary procedure and usually requires the use of calculus, however:
- To find the y-intercept, we put x = 0.
- To find the x-intercepts, we put y = 0 and solve the corresponding polynomial equation, if possible.
Let us take the polynomial y = x3 + x2 − 6x = x(x − 2)(x − 3).
The y-intercept is 0 and the x-intercepts occur when x(x − 2)(x − 3) = 0 that is, when x = 0, 2 and 3.
To get a picture of the overall shape of the curve, we can substitute some test points.

We can represent the sign of y using a sign diagram:
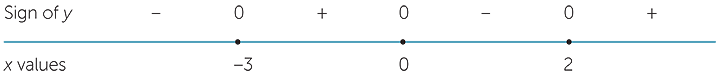
With this information, we can begin to give a sketch of the graph of y = x(x − 2)(x + 3).
The sign diagram tells us that the graph cuts the x-axis at the points x = −3, 0 and 2 and also whether the graph is above or below the a-axis on each side of these points. It does not tell us the maximum and minimum values of y between the zeroes.
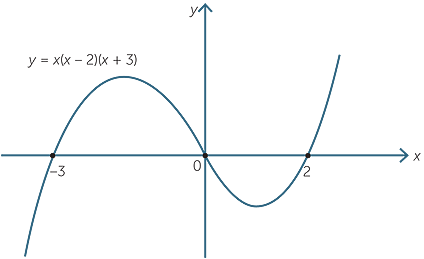
Notice that if x is a large positive number, then p(x) is also large and positive. For example, if x = 10, then y = 1040. If x is a large negative number, then p(x) is also a large negative number. For example, if x = −10, then y = −840.
EXERCISE 9
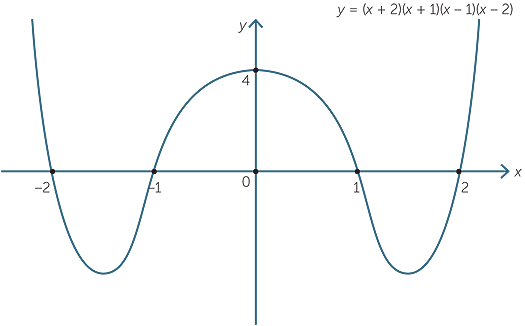
Sketch the graph of y = (x + 2)(x + 1)(x − 1)(x − 2).
Graphs of polynomials with repeated factors
Polynomial functions such as p(x) = 3(x − 1)2(x + 3)5(x − 4) which contain repeated factors require a deal of care.
If we examine, for example, the size of x4 for various values of x, we notice
- x4 is positive for both positive and negative values of x
- for values of x between −1 and 1, the size of x4 is smaller than the value of x.
Graphically this tells us that the graph of y = x4 has a minimum at x = 0 and that near x = 0 the graph is quite flat, but starts to increase sharply for x > 1 and for x < −1.
The graphs of y = x2 and y = x4 are shown for comparison.
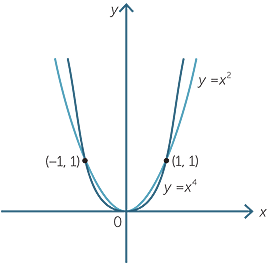
Both of these graphs have a minimum at x = 0. In the case of the parabola, we call this a vertex but we do not generally use this word for polynomials of higher degree. Instead we talk of a turning point and further classify it as a maximum or minimum.
The graphs of y = −x2 and y = −x4 each has a maximum at x = 0.
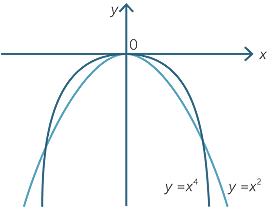
Even powers
The same phenomenon occurs for all positive even powers of x, and for even powers of (x − a). Hence near a zero of a polynomial that arises from a factor with an even power, the graph has a minimum or a maximum and is ‘flat’ near that zero.
Odd powers
The graph of y = (x − 2) cuts the x-axis at x = 2, but does not have a maximum or minimum there. Since it is a straight line, the graph is not flat at this point, indeed is has a gradient of 45° On the other hand the graph of y = (x − 2)3 behaves slightly differently at
x = 2. In the following we will consider odd powers greater or equal to 3.
Since an odd power of a negative number is negative, a sign diagram shows that the
y values of the graph of y = x3 move from negative to positive as the x values move from −1 to 1. As above, the graph is flat near the origin.
Hence the graph of y = x3 looks like:
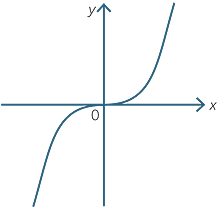
At the origin we have neither a maximum nor a minimum. The point x = 0 is called an infection point of the curve.
EXAMPLE
Plot the graph of y = 2x3(x − 2)2.
Solution
The graph passes through the origin and cuts the x-axis at x = 0 and x = 2. At x = 0 the graph has an inflection point and at x = 2 it has a minimum. The sign diagram is.

The graph is:
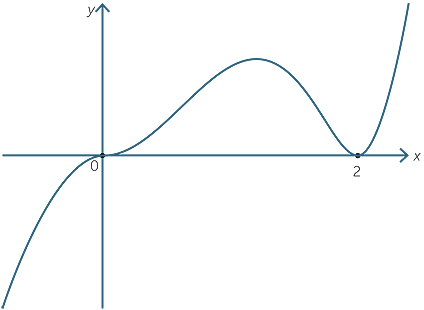
EXERCISE 10
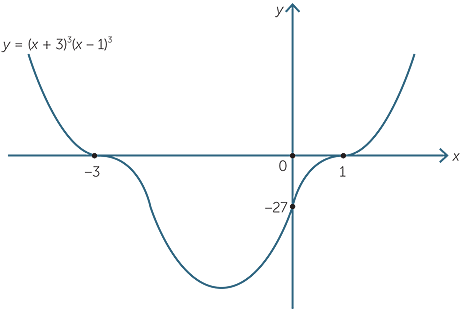
Sketch the graph of the polynomial function p(x) = (x + 3)3(x − 1)3. (You should find that the graph is symmetric about x = −1 can you see why?)
Fundamental theorem of algebra
The zeroes of a polynomial are also called the roots of the corresponding polynomial equation.
The polynomial equation x2− 4 = 0, has two integer roots, x = 2, x = −2, while the equation x2 − 2 = 0, has two real roots, x = ![]() , x = −
, x = −![]() . On the other hand, the equation x2 + 2 = 0 has no real roots. Furthermore, the equation x3 − 1 = 0, which factors as (x − 1)(x2 + x + 1 = 0), has only one real root since the quadratic x2 + x + 1 = 0 has no solutions.
. On the other hand, the equation x2 + 2 = 0 has no real roots. Furthermore, the equation x3 − 1 = 0, which factors as (x − 1)(x2 + x + 1 = 0), has only one real root since the quadratic x2 + x + 1 = 0 has no solutions.
To properly understand how many solutions a polynomial equation may have, we need to introduce the complex numbers. A complex number is a number of the form a + ib where a, b are real numbers and i2 = − 1. The complex number i is often referred to as an imaginary number. Notice that if we put b = 0, we obtain a real number and so the complex numbers contains the set of all real numbers.
Thus, although the equation x2 + 1 = 0 has no real solutions, it does have two complex solutions, x = i, and x = −i, and the polynomial x2 + 1 can be factored as (x − i)(x + i).
The great mathematician Gauss (1777−1855) gave the first proof of the following amazing result, which came to be known as the Fundamental theorem of algebra.
Theorem
Every polynomial equation of degree greater than 0, has at least one complex solution.
Given this result, it is not hard to show that:
Corollary
Every polynomial equation of degree n, greater than 0, has exactly n solutions, counting multiplicity, over the complex numbers.
EXERCISE 11
Explain how the corollary may be deduced from the theorem.
Hence, every polynomial of degree n, greater than 0, can be factored into n linear factors using complex numbers.
Note that the expression counting multiplicity means that given the polynomial equation (x − 2)3(x + 1) 2 = 0, for example, we say that the roots are x = 2, 2, 2, −1, −1. Thus we say that x = 2 is a root of multiplicity 3 and x = −1 is a root of multiplicity 2. However, the equation has only two (distinct) roots.
The vertex of a parabola is an example of a turning point. The x-coordinate of the turning point of the parabola y = ax2 + bx + c is given by x = −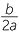 . The x-coordinates of the turning points of a polynomial are not so easy to find and require the use of differential calculus which is studied in senior mathematics.
. The x-coordinates of the turning points of a polynomial are not so easy to find and require the use of differential calculus which is studied in senior mathematics.
Suppose that we can factor the monic quadratic x2 + bx + c as (x − α)(x − β). By expanding out we can see that the sum of the roots, α + β equals −b and the product of the roots, ab equals c.
We can perform a similar exercise on monic cubics. That is, if the roots of the cubic
x3 + bx2 + cx + d are α, β, γ then it can be shown that
α + β + γ = −b, αβ + αγ + βγ = c and αβγ = −d,
These identities give relationships between the roots of a polynomial and its coefficients.
EXERCISE 12
Derive the formulas above.
The study of equations of degree greater than two goes back to Arabic mathematics. Omar Khayyam (1048−1141) spent much of his life trying to solve various cases of the cubic equation. It was not until the Renaissance that the general solution of the cubic was obtained. The precise details are sketchy, but the Italian mathematician Cardano (1501−1576) managed to prise the secret of solving the cubic out his compatriot Tartaglia and included it in his work the Ars Magna (The Great Art), published in 1545.
Cardano showed how to reduce any cubic equation to the form x3 + px + c = 0 and then, making the substitution x = u − v, reduce the problem to solving a quadratic. In practice it is easier to put x = u + v.
EXERCISE 13
Put x = y −  , in the equation x3 + ax2 + bx + c = 0 to show that the resulting equation contains no terms of degree 2.
, in the equation x3 + ax2 + bx + c = 0 to show that the resulting equation contains no terms of degree 2.
EXAMPLE
Solve x3 + 3x − 1 = 0 using the substitution x = u + v.
Solution
Rearranging the equation and substituting, we have
![]() (u + v)3 = −3(u + v) + 1.
(u + v)3 = −3(u + v) + 1.
We now expand the left-hand side and factor 3uv from two of the terms to give
![]() u3 + v3 + 3uv(u + v) = 1 −3(u + v).
u3 + v3 + 3uv(u + v) = 1 −3(u + v).
Equating the coefficients of (u + v) on both sides and equating the remaining terms,
we have
![]() u3 + v3 = 1 , 3uv = −3.
u3 + v3 = 1 , 3uv = −3.
Cubing the second equation produces
![]() u3 + v3 = 1 , u3v3 = −1 ,
u3 + v3 = 1 , u3v3 = −1 ,
At this stage, we have two numbers u3, v3 whose sum and product we know. Hence
they will satisfy the quadratic equation z2 − z − 1 = 0, which has solutions z = 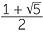 or
or
z = 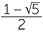 . These solutions represent the numbers u3 + v3 in either order, so taking cube roots we have the following solution to the original equation
. These solutions represent the numbers u3 + v3 in either order, so taking cube roots we have the following solution to the original equation
![]() x = u + v =
x = u + v = 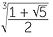 +
+ 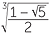 .
.
This is the only real solution to the equation.
EXERCISE 14
Use your calculator to express this in decimal form and check that it satisfies the
original equation.
The solution of the general quartic equation was found soon afterwards by Cardano’s student and protégé Ferrari. He discovered a method to reduce the problem of solving
a quartic to that of solving a cubic.
In both cases it is possible to express the solution of the given equation using square and higher roots and the usual operations of arithmetic (addition, subtraction, multiplication and division). Such a solution is often called a solution using radicals. The solutions to the quadratic equation ax2 + bx + c = 0 are x = 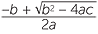 and x = −
and x = −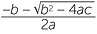 , and so the quadratic equation can also be solved using radicals.
, and so the quadratic equation can also be solved using radicals.
It was to take several hundred years before it was realised, by Abel (1802−1829) and Galois (1811−1832), that it was not possible to find the solution to the general quintic, or general higher degree equation, using radicals. Obviously, certain higher degree equations can be solved using radicals, for example x5 − 32 = 0, but this is not possible for the general case.
While Cardano’s work was a major breakthrough, there were still many unanswered questions regarding polynomials. In the 17th century Descartes found a test, known as Descartes’ rule of signs, for determining the number of positive real roots of a polynomial, while Newton discovered the so-called Newton identities that find and relate formulas for the sum of the kth powers of the roots of a polynomial. In the 18th and 19th centuries, the great mathematicians, Euler, Lagrange, Eisenstein and Gauss further extended our understanding of polynomials and polynomial equations. This led to the development of what is nowdays called modern algebra which is concerned with the study of algebraic structures.
We have seen above that when we study a polynomial, we need to specify what kind of solutions/factors we are looking for. In particular, suppose p(x) is a polynomial with degree greater than 0, and real coefficients,
- over the complex numbers p(x) factors into linear factors
- over the real numbers p(x) has all its factors either linear and/or quadratics
- over the rational numbers, it is possible to find polynomials of arbitrarily large
degree that are irreducible, that is, they cannot be expressed as the product of
two polynomials with rational coefficients, each of smaller degree.
The fundamental theorem of algebra is used to show the first of these statements. To obtain the second, we need to know the fact that when we have a polynomial with real coefficients, any complex roots will occur in pairs, known as conjugate pairs. That is, if a + ib is a root, then so is a − ib. This fact can be used to prove the second statement.
EXERCISE 15
(This requires a little knowledge of complex numbers.)
Suppose that the polynomial p(x) = anxn − an − 1xn − 1 + ... + a1x + a0 has all its coefficients real.
- a
- If α = a + ib is a solution to the polynomial equation, p(x) = anxn − an − 1xn − 1 + ... + a1x + a0 = 0, show that
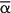 = a − ib is also a solution.
= a − ib is also a solution. - b
- Show that if x − α is a factor of p(x), where α = a + ib is a complex number, then the quadratic (x − α)(x −
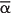 ) is also a factor of p(x) and that (x − α)(x −
) is also a factor of p(x) and that (x − α)(x − 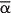 ) has real coefficients.
) has real coefficients. - c
- Deduce that every polynomial with real coefficients can, in theory, be factored as a product of linear and/or quadratic factors, with real coefficients. (Note that in practice this can be a very difficult task to perform.)
Eisenstein (c. 1850) came up with the following ingenious test for irreducibility of polynomials over the rationals.
Consider the polynomial p(x) = anxn − an − 1xn − 1 + ... + a1x + a0, where all the coefficients are integers. Suppose that we can find a prime number p that does not divide the leading coefficient an, but which does divide all of the other coefficients. The test says that if the square of that same prime does not divide the constant term, that is, p2 + a0 then p(x) is irreducible over the rational numbers.
EXAMPLE
The polynomial p(x) = 5x7 + 6x6 − 15x 4 + 12x − 21 satisfies Eisenstein’s criteria with the prime p = 3 and so p(x) cannot be expressed as the product of two polynomials each of smaller degree with integer coefficients. That is, p(x) is irreducible.
EXERCISE 16
Explain how to construct a polynomial of arbitrarily large degree that cannot be factored over the rationals.
Maclaurin Series
In the 17th and 18th centuries, mathematicians made the remarkable discovery that functions such as y = sin x and y = cos x could be expressed using ‘infinite polynomials’, that is, polynomials whose powers of x continue indefinitely. These are called power series. Thus, for example,
![]() sin x = x −
sin x = x −  +
+  −
− 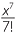 + …,
+ …,
where the obvious pattern continues forever. The notation n! (read as n factorial) is an abbreviation for n(n − 1)(n − 2) … 3.2.1. Thus 5! = 5 × 4 × 3 × 2 × 1 = 120. These infinite series are often referred to as Maclaurin series and have very wide application in both mathematics and physics.
There still remain today unsolved problems related to polynomials. The appendix below discusses in broad outline a remarkable application of polynomials to modern telecommunications.
An application of polynomials to error-correcting codes
Digitising information
Information is usually digitized by converting it to a sequence of 0’s and 1’s. For example, the ASCII code for the digit 1 and letter A are ‘1’ ![]() 1000110, and ‘A’
1000110, and ‘A’ ![]() 1000001. We will assume here that all messages under consideration are finite sequences of 0’s and 1’s.
1000001. We will assume here that all messages under consideration are finite sequences of 0’s and 1’s.
When your mobile phone sends or receives messages, or data is sent from satellites deep in space, information may be lost or corrupted along the way to its destination.
Since the information is sent as sequences of 0’s and 1’s, a ‘corrupted’ 0 becomes a 1 and vice versa.
A simple check for errors is to add in a check digit so that the string has an even number of 1’s, and hence the sum of the digits is even.
Thus we encode 1 as 10001101 and A as 10000010.
Now if a byte is transferred and one of the bits is corrupted, then the number of the 1’s becomes odd, and so the receiver can ask for a retransmission.
This code can detect one error, but cannot correct it.
A polynomial modulo 2 is a polynomial whose coefficients are either 0 or 1. Arithmetic is then performed modulo 2 so that 0 + 1 = 1 + 0 = 1 and 1 + 1 = 2= 0.
We perform addition modulo 2.
EXAMPLE
If p(t) = t3 + 1 + 1, q(t) = t4 + t3 + t2 + 1
Then p(t) + q(t) = t4 + 2t3 + t2 + 2t + 2 = t4 + t2.
Multiplication is done similarly.
Solution
p(t) = t3 + 1 + 1, q(t) = t + 1, then
p(t) × q(t) = (t3 + t + 1)(t + 1) = t4 + t3 + t2 + 2t + 1 = t4 + t3 + t2 + 1
Coding
We now fix a polynomial m1(t) = t3 + t + 1.
This polynomial cannot be factored modulo 2 since the only possible roots are 0 and 1 and neither work.
We now suppose that the polynomial m1(t) has a root a. This is, a has the property that
α3 + α + 1 = 0 or α3 = α + 1 (Recall that modulo 2, −1 = 1)
This number α is very interesting and using the equation above, we can make up a table of its powers.
Power | Simplified form
| α | | α | |
| α2 | | α2 | |
| α3 | | α + 1 | |
| α4 | | α2 + α | |
| α5 | | α2 + α + 1 | |
| α6 | | α2 + 1 | |
| α7 | | 1 |
For example, to obtain α5 we multiply α4 = α2 + α by a giving α5 = α3 + α2 and replace α3 with α + 1 to obtain α5 = α + 1 + α2.
Thus, we can write all the powers of α as combinations of 1, α and α2 (!!)
Now for the codes.
We start with a message (a, b, c, d) in binary of length 4 add in 3 check digits to obtain
(a, b, c, d, x, y, z). We use these as the coefficients of the polynomial
![]() p(t) = at6 + bt5 + ct4 + dt3 + xt2 + yt + z.
p(t) = at6 + bt5 + ct4 + dt3 + xt2 + yt + z.
The digits x, y, z are chosen so that p(t) is divisible by the polynomial m1(t) = t3 + t + 1
Since a is a root of m1(t) it is also a root of p(t) and so p(a) = 0.
EXAMPLE
Take the message (1, 0, 0, 1) and encode it as (1, 0, 0, 1, x, y, z). Converting to a polynomial, we have
| p(t) | = t6 + t3 + xt2 + yt + z. | |
| Substituting t = a and using the table to simplify we have | ||
| p(a) | = a6 + a3 + xa2 + ya + z. | |
| = (a2 + 1) + (a + 1) + xa2 + ya + z | ||
| = a2 (x + 1) + a(y + 1) + z. | ||
Now if we take x = 1, y = 1, z = 0 then p(a) will be zero. Hence we encode the message
(1, 0, 0, 1) as (1, 0, 0, 1, 1, 1, 0). We will call the polynomial corresponding to the sent message C(t) and so C(a) = 0.
Suppose that one error occurs in the fifth number from the left so we receive the message (1, 0, 1, 1, 1, 1, 0).
Thus the t4 coefficient is incorrect and to the polynomial for the received message is
![]() R(t) = C(t) + t4
R(t) = C(t) + t4
Substituting t = α we obtain
![]() R(α) = C(α) + α4 = α4
R(α) = C(α) + α4 = α4
and so we know where the error is.
In general, if there were exactly one error in the th digit, we would receive
![]() R(t) = C(t) + ti.
R(t) = C(t) + ti.
Then R(α) = C(α) + αi = αi and so the calculation of R(a) gives the position of the incorrect digit.
If R(α) = 0 then there were no errors. This process, of course, assumes that at most 1
error occurred.
EXAMPLE
Assuming at most one error, correct and decode the message (1, 0, 0, 1, 0, 0, 1).
Solution
Converting to polynomials, we have
![]() R(t) = t6 + t3 + 1
R(t) = t6 + t3 + 1
and so
![]() R(α) = α6 + α3 + 1 = α2 + 1 + α + 1 + 1 = α2 + α + 1 = α5
R(α) = α6 + α3 + 1 = α2 + 1 + α + 1 + 1 = α2 + α + 1 = α5
So the corrected message was (1, 1, 0, 1, 0, 0, 1) which decodes as (1, 1, 0, 1).
Correcting more than one error
The coding and correcting procedure outlined above only works if at most one error occurred in the transmission.
The polynomial method can be extended to detect and correct more than one error.
The details of these codes is slightly more complicated, but uses the same ideas developed above.
The codes used to perform multiple error correcting are called BCH codes and were discovered (independently) by Bose and Chaudhuri (in 1960) and Hocquenghem (in 1959) -hence the name BCH.
While the arithmetic now becomes very hard, it is easily performed by a computer, and codes can be constructed that can detect and correct an arbitrary number of errors.
The modern error correcting codes used in mobile phone technology are more sophisticated again, but essentially use the kinds of machinery which I have outlined above.
More recently, Reed-Solomon codes, which are a type of BCH code, have been used in applications such as satellite communications, compact disk players, DVDs and disk drives.
EXERCISE 1
Leading term: anxn
Leading coefficient: an
Degree: n
Constant term: a0
EXERCISE 2
a![]() 4x6 − 4x4 + 4x3 + x2 − 2x + 1
4x6 − 4x4 + 4x3 + x2 − 2x + 1
b![]() i
i![]() …. the sum of the degrees of the polynomials
…. the sum of the degrees of the polynomials
![]()
![]() ii
ii![]() … the product of the constants
… the product of the constants
EXERCISE 3
5x4 − 7x3 + 2x − 4 = (x2 − 2)(5x2 − 7x + 10) + (−12x + 16)
EXERCISE 4
a = 18
EXERCISE 5
a = −33 and b = −15
EXERCISE 6
If P(a) = 0 then a0 = − anan − an−1an−1 ….−a1a. Hence a divides a0.
EXERCISE 7
2x2(x − 3)2(x − 5)
EXERCISE 8
x= 0 or x = 3 or x = 5
EXERCISE 9
EXERCISE 10
EXERCISE 11
For the polynomial equation P(x) = 0 there is a solution x = a by the theorem. Hence x − a is a factor of P(x) and P(x) = (x − a)Q(x). The equation Q(x) = 0 also has a solution and so a new linear factor can be found by the theorem.
EXERCISE 12
(x − α)(x − β)(x − γ) = x3 − (α + β + γ)x2 + (αβ + αγ + βγ)x + αβγ = x3 + bx2 + cx + d
Hence the result, b = −(α + β + γ) , c = (αβ + αγ + βγ) and d = αβγ
EXERCISE 13
y3 − 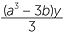 +
+ 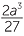 −
− 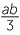 + d
+ d
EXERCISE 14
- a
- Take conjugates of both sides. The conjugate of a real is the same real.
- b
- An immediate consequence of a and the factor theorem and the fact that both the sum and product of a complex number and its conjugate are real.
- c
- The fundamental theorem and b gives the result
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

