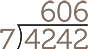The Improving Mathematics Education in Schools (TIMES) Project
Children learn to count before they learn to write numbers, just as they learn to speak before they learn to write words. Even very young children understand that there are special words to be said when counting and may be able to tell you how old they are, or point to numbers in their environment. They might use number words, though often incorrectly. For example, they may say “One, two, one, two…” as they touch a number of objects to be counted.
Children begin school with a variety of experiences, indeed the range of mathematical skills and understanding in any one early-years classroom can be quite vast. Children’s prior learning about number will have been influenced by their family, whether or not they attended pre-school or formal child-care, and their language and social development.
Typical exposure to numbers occurs via a variety of media, through songs, play, interaction with adults and other children, picture storybooks and television programs. When a small child walks down the steps s/he may count them. A long trip in the car is made more enjoyable by counting yellow cars and the child who successfully places the right number of potatoes into a plastic bag at the supermarket is learning to count as well as being helpful. There are many wonderful stories, songs and rhymes that involve mathematical themes and these are useful in enhancing the learning of mathematics for children.
Children arriving for their first year of school may be able to:
- Recite the numbers up to 20 in order
- Write the numerals 0 to 9
- Grasp the connection between the numeral ‘3’, the word ‘three’ and a picture such as
 or
or 
Teachers and parents should take care that certain understanding is evident before proceeding to tasks that are more cognitively demanding. It is advisable that students who arrive at school with a firm grasp of number concepts are also catered for, with suitably challenging tasks and the introduction of new concepts as appropriate.
Numeracy and literacy are essential skills in modern society. Just as we need the alphabet to write down words and sentences, so we need a notation to write down numbers. We use a base-ten place-value notation to write numbers. It was developed over several centuries in India and the Arab world, so we call it Hindu-Arabic notation. The place-value nature of Hindu-Arabic notation enabled the development of highly efficient algorithms for arithmetic, and this contributed to its success and wide acceptance.
Hindu-Arabic numerals exhibit some of the qualities that make mathematics so
powerful, namely
- they can be used by understanding a small number of ideas, and
- they can be generalized beyond the original setting for which they were devised.
To illustrate the second point, the notation was developed to express whole numbers,
but it extends to the representation of fractions and decimals.
A solid understanding of numbers and arithmetic is essential for the development of later concepts including fractions and algebra.
Hindu-Arabic numerals are a decimal, or base-ten, place-value number system with the ten digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 as fundamental building blocks. It is important that students build an understanding of the numbers up to ten before they progress further.
We will make a distinction between a number and a numeral. A number is an abstract concept, whereas a numeral is a symbol that relates to a quantity that we assign to it. Thus the number three is the abstract concept common to three chairs, three crayons, and three children, whereas the symbols 3 and III are numerals for the number three.
For example, the numeral ‘3’ relates directly to the number of stars shown here .
Although the concept of number is universal (there are the same number of stars in ![]() regardless of whether you count in English, Spanish or Mandarin) the number names and numerals are a necessary, but arbitrary, label invented by humans. Assigning a numeral to a number of objects, writing a symbol that relates to the number of items in the set, has happened in a variety of ways across different cultures for thousands of years. So, while some students may have a good sense of number from an early age, they all need to learn the number names and numerals.
regardless of whether you count in English, Spanish or Mandarin) the number names and numerals are a necessary, but arbitrary, label invented by humans. Assigning a numeral to a number of objects, writing a symbol that relates to the number of items in the set, has happened in a variety of ways across different cultures for thousands of years. So, while some students may have a good sense of number from an early age, they all need to learn the number names and numerals.
Subitising
The ability to identify quickly the number of objects in a small set is known as subitising. This is different to counting and requires a rapid response. Before their first birthday babies can make judgements about the relative sizes of sets of objects. They react differently when two sets of the same size are presented compared to when two sets with different amounts are presented. The skill of subitising stays with us and is used in helping us to recognise numbers displayed on dice and playing cards, for example.
One-to-one correspondence
It is not necessary to name the numbers to tell if one set has more or less than another. Early understanding of ‘more than’ and ‘less than’ can result from simple matching activities that help children see that one set is larger (or smaller) than another. Using one-to-one correspondence the child matches up the elements of the two sets, pairing each item in one set with exactly one element in the other set. The child can now tell if the sets are ‘the same’ or ‘different’ in number and which is larger or smaller.
In the example below, it is not easy to immediately say if there are more puppies or kittens,

but the answer is clear when they are lined up with one-to-one correspondence.


Matching activities will help a young child develop one-to-one correspondence. Activities may include matching pairs (of socks or shoes), distributing materials to each member of a group, sharing food or toys equally amongst classmates, placing one toy on top of each of several blocks, returning materials to shelves, setting the table, matching object to object (for example, matching people to their coats and hats) and matching a picture of a quantity to a set of objects with the same number of items. Gradually, the child recognizes that one group of things can have the same number of elements as another group and abstracts the concept of number.
THE NEXT NUMBER IN THE SEQUENCE
A two-year-old’s favourite number is two until they have a birthday, when they quickly learn what comes next in the sequence. Once a child has understood that the number two can be shown by the numeral ‘2’ and by holding up two fingers, they need to progress onto the idea of building to the next number. This is essentially a mastery of the idea that we can obtain the next number by the addition of ‘one more’ and can be achieved by lots of experience counting with manipulatives.
Recitation of a list of numbers is not necessarily counting. Many children can recite the number names when they arrive at school. Some of them may be able to recite them in order up to 20 or more. It is likely, however, that some of them are only just beginning to understand that each numeral and its corresponding number word represent a quantity that is fixed. For children to be considered as having the ability to count, there are certain behaviours that must be evident; each of these is essential to counting.
One-to-one correspondence with number names and objects
The understanding that we use different number names for each object included in a count is a major milestone. A child who counts a set of objects by saying “four, two, one” has understood the need for one-to-one correspondence, as has the child who correctly counts “one, two, three”. A child who counts “three, two, three” has not used a unique number name for each object and neither has the child who uses more number names than objects and counts “one, three, six, seven, two, four” when counting these stars ![]() .
.
Stable order
To count accurately and reliably, it is important to say the number names in the right order and without skipping any numbers. The ability to assign the number names in order to objects being counted and without skipping any numbers, is known as the stable-order principle. Children may begin to do this by counting their fingers, counting the number of ‘sleeps’ until their birthday or the number of peas left on their plate.
Cardinality
One of the deep observations about counting is that when you set up a 1-1 correspondence between the number names in their correct order and the set of objects you are trying to count, then the last number name you say is the cardinality (or size) of the set.
We can help children develop the understanding of cardinality by involving them in activities where they answer questions about ‘how many’. They need not only to be able to say the counting names in the correct order, but also to count a group of, for example, seven objects and say that there are seven. Counting activities should have some basis in reality, giving a purpose to counting. For example, we can create a need to count by involving children in food preparation. They will need to know how many people, plates or apples in order to complete the task.
Once a child has a sense of cardinality, then we can involve them in matching activities where a number word is matched to a quantity and the numeral that belongs to it.
|
|
|
|
|
4 |
7 |
2 |
In the activity above, students count the items and give a name to the total number in the set. Using the last number-name that was spoken as a tag to label a quantity is a big step in developing ‘number sense’.
Zero
Children may be accustomed to using words to describe the absence of something. For example, “I have no lollies left.”, “There is nothing on my plate.” or “The olive jar is empty.” We use the word zero to describe ‘nothing’ and we use the symbol ‘0’ when we write it in numerals.
Zero is used in a place-value context also. For example in the number 208, the zero indicates that there are ‘no tens’ in the number.
Later children will come to understand the effect of adding and subtracting zero. For some children their inclination is to think that adding makes collections bigger, and subtracting makes them smaller. As with introducing addition and subtraction with small numbers, acting out situations where zero is added to or subtracted from a collection can help in developing the understanding that this will have no effect on the size of the collection.
Counting objects in any order or arrangement
The number of elements in a set does not depend on the way the objects are presented or the order in which they are counted. Knowing that the order in which objects are counted has no relevance to the actual number of objects in the group of objects is known as the order-irrelevance principle.
One way of testing to see if children have developed this understanding is to re-arrange
a set of objects that they have just counted, and ask them to count again.
Ordering is the basis of our number system. The ability to place quantities in order of increasing (or decreasing) size demonstrates a deep understanding of how the number system fits together. A child who understands that 2 is bigger than 1, 3 is bigger than 2 and so on, is demonstrating sound conceptual knowledge of the number system. Beginning with the idea of one more or one less, pre-school children become adept at moving around on a mental number line. Start by asking what is one more than their age, then build from there. The idea of ‘one more than’ and ‘one less than’ should be developed before ‘two more than’ and ‘two less than’ and so on. Encourage the use of strategies to help, such as using fingers or objects. Classroom activities where ordering from smallest to largest (or the reverse) is the prime skill should be undertaken to help students develop a sense of order. For example, ordering students from tallest to shortest, ordering strips of paper that measure the hand-span of each student from smallest to largest or writing a ‘favourite number’ on a card and pegging it on a number line in the correct order.
Discussion about breaking numbers apart and putting them back together helps children see that numbers can be ‘made’ from other numbers. It requires them to make connections between numerical ideas and prepares the way for arithmetical thinking. The child should be involved in activities that require them to pull a number apart and put it back together, helping them learn more about how the number system works and giving them the opportunity to demonstrate their understanding of cardinality and addition.
Classroom Activity
On my fingers
Ask the child to show you the number five on their hands. There are many ways to do this and soon they will see that five is made up of 1 and 4, 2 and 3, 3 and 2, 4 and 1 and, hopefully, 5 and 0.
There are many different ways to show the numbers to ten using fingers and thumbs.
|
Number of fingers |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Number of ways |
1 |
10 |
45 |
120 |
210 |
252 |
210 |
120 |
45 |
10 |
1 |
From the table above, we can see that there are 210 different ways to show the number 4 on our hands. It is a convention that there is 1 way of showing 0. It is probably surprising to you that there are so many ways of showing 5 with your fingers.
Classroom Activity
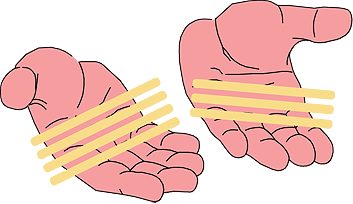 Sticks in hands
Sticks in hands
Playing with sticks (or counters or pebbles) allows children to see part whole relationships. For example, 7 sticks in two hands shows that 7 is made from 4 and 3.
Classroom activity
Block patterns
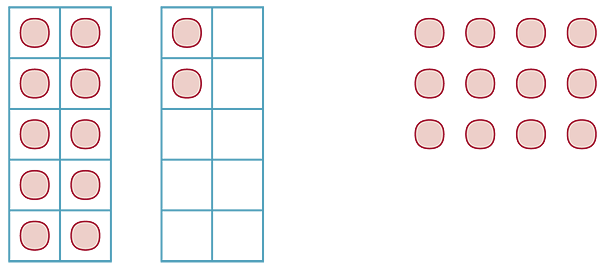
Provide blocks or counters and ask children to arrange the same number of counters in different ways. For example, take six blocks and arrange them in different patterns, like two rows of three, three rows of two, a triangle, and other more elaborate structures. At this point, we are really dealing with ‘six’ as a characterisation of the number of objects in the set, and the patterns that we obtain are all characteristic of six.
Once the numbers below ten are established, the next goal is to look at the numbers from ten to twenty. We want students to see the importance of ten and as a result, many of the activities they do in the early years of school are focussed on building from ten and using ten as a countable unit.
By the time they come to school they may know 30, 40 or 60 from speed limit signs. Students often begin using manipulatives that can help illustrate the importance of ten at this point. We want them to come to think of these numbers as ten and one, ten and two, ten and three and so on.
 Students begin to record the numbers with some
Students begin to record the numbers with some
understanding of the ‘ten’ and the ‘more than’ in
place-value columns. So 13 is written
Eleven, twelve, thirteen
The English words for 11, 12 and 13 appear to be unrelated to the numbers that follow, but the etymology tells us that this was not always so. In each case, the base word is a version of ten or means ‘ten more than’. The word eleven originated from the Germanic ainlif meaning “one left” (after ten is taken). The word twelve then comes from twalif, meaning that two is left after ten is taken. Only the remaining first two letters of twelve tell us that it is connected to the number two.
Thirteen originates from the Old English reotiene (from reo meaning ‘three’ and tene which translates as ‘ten more than’).
To ensure that students develop the concepts related
to ‘ten more than’ we encourage them to practice
modelling numbers using materials such as icy-pole
sticks and counters.
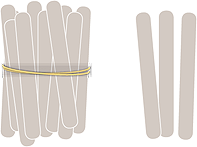
Tens-frames give a sense of the ten and the more than:
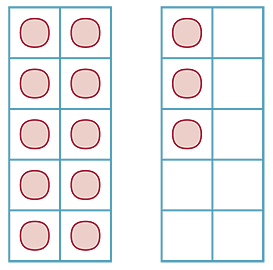
The teen numbers
Once we get past the number thirteen, there is a pattern in the number words that helps us understand the place value of the collection we are counting. This is more difficult in English than in some other languages.
In Mandarin, there is a unique symbol for each of the numbers to ten, then these are combined to make the numbers to 99.

The number 11 is written using the numerals for 10 and 1
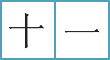 shi yi
shi yi
The number 12 is written using the numerals for 10 and 2
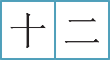 shi er
shi er
The number 13 is shi san (ten and three), 14 is shi si (ten and four), and so on. When you get to 20, you say er shi (two tens), and then 21 is er shi yi, (two tens and one), 22 is er shi er (two tens and two). So 87 is ba si qi.
PLACE VALUE: TWO ‘TENS’ AND BEYOND
Students should experience counting using manipulatives such as icy-pole sticks and counters with numbers that are large enough for them to see the need to make and use ‘tens’. We want them to become accustomed to organising the items they are counting into ‘tens’ as an efficient means of finding the total of the count.
So, a collection such as this

is organised in tens for easy counting

and the tens are counted first: “Ten, twenty, thirty, thirty-one, thirty-two, thirty-three, thirty four.” There are thirty-four counters.
This can also be demonstrated using base-ten arithmetic blocks,

on the number line,

and using tens frames.

The place-value columns reinforce the idea of ‘how many tens’ and ‘how many ones’.
So 34 is recorded in place-value columns as follows:
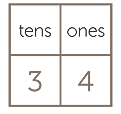
When the children are comfortable with the numbers beyond ten, we can extend some of the activities for developing number sense that were used earlier. This is a good teaching strategy, as the children are already comfortable with the activity with smaller numbers.
Classroom activity
Block patterns
Provide blocks or counters and ask children to arrange the same number of counters in different ways.
For example,
Classroom activity
Sticky notes
Prepare overlapping sticky notes or place-value cards to reveal the place value
of digits in numbers.

This shows that 34 = 30 + 4
Children who have developed the ability to count should continue to do so, expanding their repertoire beyond ten or even one hundred or one thousand. Counting forwards and backwards from different starting points including zero helps with fluency with numbers, is connected to arithmetic and can be used with fractions and decimals.
Counting backwards
Many children will be able to recite the backwards counting sequence from ten and will even add zero on the end “10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0!” as in a countdown for a rocket taking off, but understanding of what is happening as we subtract one from the set to show the number before should be reinforced by using hands-on materials. Going up and down by one and by two prepares the way for addition and subtraction.
Whisper counting
Whisper counting is a precursor to skip counting. When whisper counting by 3s, you say every third number loudly. Gradually say the skip counted numbers louder and louder and the other numbers softer and softer. Increase the speed of counting until the child can count entirely in skip count mode (3, 6, 9, 12, 15...). You can also clap (hop, ring a bell, etc.) instead of whispering as you move to skip counting. Give children time to develop and feel successful with one type of skip-count before moving to the next one.
Classroom Activity
Whisper counting
The teacher and the child each take a role in counting together.
Start by taking turns to count
a![]() I say 1, you say 2, I say 3, you say 4, …
I say 1, you say 2, I say 3, you say 4, …
b![]() I say 1 very quietly, you say 2, I say 3 very quietly, you say 4, …
I say 1 very quietly, you say 2, I say 3 very quietly, you say 4, …
c![]() You imagine me saying 1, then you say 2, then you image me saying 3,
You imagine me saying 1, then you say 2, then you image me saying 3,
then you say 4, …
d![]() Repeat all these steps with the teacher starting at 2, and then at 0.
Repeat all these steps with the teacher starting at 2, and then at 0.
Skip counting
Skip counting is an essential step in the development of arithmetic, so there is a great deal to learn from it. Start with counting by 2s, then 10s, 5s, and finally by 3s, 4s and so on.
Classroom Activity
Counting by 2s
1 a Ask the child to arrange ten blocks in two equal rows and then count to check that there are five columns.
b Now have the child count the ten blocks counting each column in turn.
c Now make the big leap and get the child to count the blocks in twos by pointing to each column in turn and running through the even numbers. The really big idea here is that the final number, 10, is indeed the total number of blocks, and there needs to be quite a bit of checking backwards and forwards while the child makes certain that this ‘clever’ method of counting does indeed end up with the total number of blocks.
d Repeat with other even numbers
2 The next step is adding two with blocks.
a Put out the eight blocks, and repeat everything.
b Bring up two more blocks and ask how any blocks there are now. You might notice that s/he will dutifully count the blocks in ones and get ten.
c Invite the child to count the blocks in twos, and be delighted when she gets the same answer.
d Repeat this many times, until eventually the child, on being faced with ten blocks
in two rows, and another two blocks, will claim immediately that there are 12.
Make sure that s/he checks!
The number 100 is an important one for children to understand. It is the next place in the place value system after ‘tens’, as with the number 834 shown below
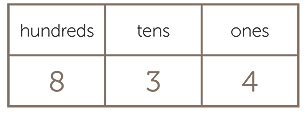
One hundred has some interesting properties.
 We can count to 100 by tens. So a child would say 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
We can count to 100 by tens. So a child would say 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.- 100 can be ripped apart in many different ways.
- 100 can be arranged into a square array made
from ten rows of ten.
Classroom Activity
Rip apart 100
Give children a zip-lock bag and a number of counters, icy-pole sticks or coloured match sticks. Ask them to count out 100. Use the counters to show how 100 can be ripped apart in many different ways. Ask the children to make statements about the different ways they have ‘ripped part’ the number 100. For example, 87 + 13 = 100
As the numbers that students can cope with expands, so naming of numbers and the structure of the place-value system expands to accommodate larger and larger numbers.
Each digit in a number has a place value depending on its position. These positions can be thought of as columns labelled by powers of ten, with the powers increasing from right to left as illustrated in the following table.

When reading Hindu-Arabic numerals, the digit with the largest place value is read first. Thus the number 7352 is read as “seven thousand, three hundred and fifty-two”, and we think of it in columns as illustrated in the following table.
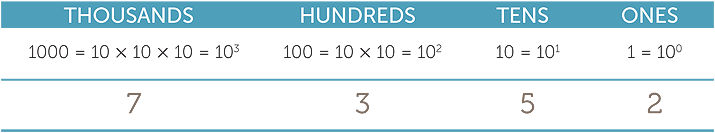
These labels are made explicit when we write numbers in expanded form. For example, 7352 = 7 × 1000 + 3 × 100 + 5 × 10 + 2.
Classroom activity
Sticky notes
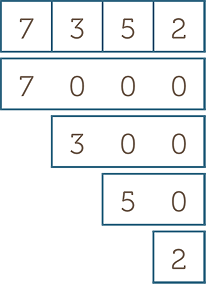 The sticky notes activity can be extended to
The sticky notes activity can be extended to
any number of places. Prepare overlapping
sticky notes or place-value cards to reveal
the place value of digits in numbers.
This shows that 7352 = 7000 + 300 + 50 + 2
The importance of zero
The digit 0 is essential in the Hindu-Arabic system because it acts as a place-holder. In the number 302, the 0 tells us that there are ‘no tens’.
Multiplying a number by ten shifts each digit one place to the left. Because there is now nothing in the ones column, we put a 0 in that column as a place-holder. The following table illustrates the process for 35 × 10 = 350.

Dividing by ten shifts the digits one step to the right, and requires decimals unless the last digit in the original number was 0. The following table illustrates this process for 350 ÷ 10 = 35.

Conventions about spacing and naming
A number with many digits can be hard to read. We cluster the digits in groups of three, starting from the ones place, and separate different groups by a thin space. By convention we do not put a space in a four-digit number. Thus we write 7352, but 17 352 and 2 417 352.
The nested method that we use to name the columns enables us to read very large numbers using a few basic words such as thousands and millions.
Classroom Activity
Use place-value houses to gather digits into groups of three and to aid in the naming of larger numbers.

So we write the number shown in the place value houses above as 1 427 596 and we say one million, four hundred and twenty-seven thousand, five hundred and ninety-six’. Converting between words and numbers and vice versa are important skills.
The following table summarises some column names and their values.
|
Column value |
Name |
|||||
|
1 |
100 |
one (unit) |
||||
|
10 |
101 |
ten |
||||
|
100 |
102 |
hundred |
ten × ten |
|||
|
1000 |
103 |
thousand |
ten × hundred |
|||
|
10 000 |
104 |
ten thousand |
||||
|
100 000 |
105 |
hundred thousand |
||||
|
1 000 000 |
106 |
million |
thousand × thousand |
|||
|
10 000 000 |
107 |
ten million |
||||
|
100 000 000 |
108 |
hundred million |
||||
|
1 000 000 000 |
109 |
billion |
thousand × million |
|||
|
1 000 000 000 000 |
1012 |
trillion |
||||
|
10100 |
googol |
|||||
The convention is slightly different when we write about money. It is standard accounting practice to separate the groups of digits by a comma. For example, the average annual salary in Australia was close to $64,200 in 2009. This can cause confusion for two reasons.
Firstly, people often see numbers in the context of money and tend to always write large numbers with commas to separate groups of digits.
Secondly, the use of a comma is not a world-wide standard. In continental Europe the groups of digits are separated by points and what we call a decimal point is replaced by a comma. The average annual salary in Spain might be 21.500 euros, but a coffee might only cost 1,20 euros.
Children’s understanding of place value improves dramatically once they start working with the formal algorithms for addition, subtraction, multiplication and division. These algorithms will be covered in other modules. When using the algorithms there are a number of common errors related to place value.
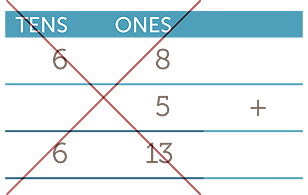
For example, a common error is to enter two digits into a single column when carrying out the addition algorithm.
|
|
|
|
|
(Correct |
(Wrong) |
Another common error is forgetting to use 0 as a place marker when performing division.
|
|
|
|
|
(Correct) |
(Wrong) |
As we mentioned in the motivation, the existence of fast and efficient algorithms for arithmetic is a major advantage of the Hindu-Arabic numerals.
This module has dealt with whole numbers. Once students have mastered whole numbers, we introduce them to integers (the whole numbers together with the negative numbers −1, −2, −3, …) and rational numbers (positive and negative fractions).
The development of the concept of number can be described with the aid of the following diagram.

School mathematics normally follows the historical development of numbers and introduces students first to whole numbers then to positive fractions, then to integers,
and finally to the rational numbers.
Note that when we discuss the historical development of this topic we are always talking about the same numbers. The history of numeration is all about the evolution
of numerals.
Early civilizations developed different ways of writing numbers. Many of these ways were cumbersome and made it hard to do arithmetic. The most basic and oldest known system of numeration involves tally marks.
THE BABYLONIANS
The two earliest civilisations known to have developed writing and written number systems are the Egyptian and Mesopotamian civilisations centred on the modern countries Egypt and Iraq. Mesopotamia probably began to develop as small city-states between 6000 and 7000 years ago.
For various reasons, Mesopotamian mathematics is called Babylonian mathematics and quite a lot is known about it and its users, despite the fact that to date the only clay tablets discovered date from about 1600 BC, 1000 BC and 300 BC.
The Babylonian number system was in base 60 so the number 1, 5, 13 is
1 × 602 + 5 × 60 + 13 = 3913 in base 10.
This, of course, means that 60 digits from 0 to 59 are needed. In 1600 BC a space was used as a place holder as in 1, 0, 13 but by 300 BC the symbol 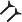 was used as a place holder. The remaining 59 digits were created using a base 10 system. So 34 was drawn as 10, 10, 10, 1, 1, 1, 1 in a neat character grouping. By 1600 BC the system also represented sexagesimal (base 60) fractions so, depending on the context, 1, 5, 13 could also represent
was used as a place holder. The remaining 59 digits were created using a base 10 system. So 34 was drawn as 10, 10, 10, 1, 1, 1, 1 in a neat character grouping. By 1600 BC the system also represented sexagesimal (base 60) fractions so, depending on the context, 1, 5, 13 could also represent 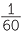 +
+ 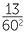 +
+ 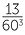 . This sexagesimal number system had all the features of the modern decimal place-value system except for the sexagesimal point.
. This sexagesimal number system had all the features of the modern decimal place-value system except for the sexagesimal point.
THE EGYPTIANS
The Egyptians used a system of numeration based on powers of ten, but it was not a place-value system. They used the following hieroglyphs for powers of ten and simply drew as many of each as they needed.
|
|
|
|
|
|||
|
1 |
10 |
100 |
1000 |
10 000 |
100 000 |
106 |
For example, the number 7352 was written as:
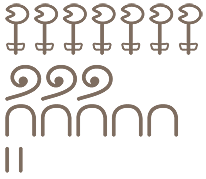
Later, when the Egyptians started writing on papyrus, they developed a short-hand system based on hieratic numerals illustrated in the table below. Hieratic means “of priests” and reflects the close connection between religion and education at the time.
Hieratic numerals allowed people to write numbers more succinctly and with greater speed than before.

ROMAN NUMERALS
Once civilisations moved from hieroglyphic (picture-based) to alphabet-based writing, letters were used as numerals. The best-known example is the system of Roman numerals, but earlier systems were also developed using the Greek and Hebrew alphabets.
The basic numerals are listed in the following table:
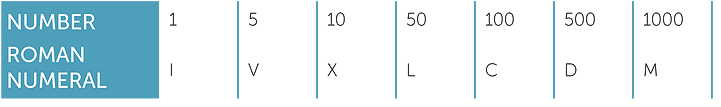
Roman numerals are added whenever they were listed in decreasing order, so LXVII represents 50 + 10 + 5 + 1 + 1 = 67. The value of a numeral does not change depending on its location, except in a very local sense. If a numeral is placed immediately to the left of the next-biggest numeral then the smaller numeral is subtracted from the larger; so XI represents 10 + 1 = 11 whereas IX represents 10 − 1 = 9, but 49 would not be written as IL. Forty-nine is written as XLIX.
HINDU-ARABIC NOTATION
The Hindu-Arabic notation was probably developed in India. A place-value system using 9 digits and a space or the word kha (for emptiness) as place marker was used in India the 6th century AD. By the 9th century the system had made its way to the Arab world (including Persia and Al-Andalus in what is now Spain). The digit 0 evolved from “.” and was used in both Madhya Pradesh (Northern India) and the Arab world by the 10th century.
Leonardo of Pisa, known as Fibonacci, learned to use the notation from merchants in Africa when he was a boy. His book, Liber Abaci, written in 1202 contained a description of the notation. This book popularized the Hindu-Arabic system in Europe. At about the same time, Maximus Planudes wrote a treatise called The Great Calculation entirely devoted to the Hindu- Arabic notation and the algorithms of arithmetic.
It is no coincidence that the word digit also means the fingers and thumbs on our hands. The fact that we use a base-ten place value system is almost certainly a consequence of a natural tendency to count on our fingers.
The inconsistencies in the use of commas and points to separate groups of digits or whole numbers from fractional parts when writing about money is one of several examples of cultural differences in mathematics. Countries colonized or influenced by Britain (including the USA, India and Malaysia) use a comma to separate blocks of 3 digits when writing amounts of money, whereas countries colonized or influenced by continental European countries (including South America and Vietnam) use a point. In Canada, a comma is used in the English speaking west of the country and a point in the French-speaking east. These types of considerations should be taken into account when working with families from other cultural backgrounds.
The Child’s Understanding of Number, R. Gelman, and C. R. Gallistel, Harvard University Press, (1978)
Children’s understanding of mathematics, K.M. Hart (Ed.), London: John Murray, (1981)
Young Children as Mathematicians: Theory and Practice for Teaching Mathematics, Dianna Mannigel, Wentworth Falls NSW. Social Science Press, (1992)
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()