The Improving Mathematics Education in Schools (TIMES) Project
Experiences before starting school
On their arrival at school, small children are likely to be aware that the world of numbers exists, and may be able to:
- Recite the numbers up to 20 in order.
- Write the numerals 0 to 9.
- Grasp the connection between the numeral ‘3’, the word ‘three’ and a picture such as
 or
or  .
.
Addition and subtraction are two of the ways we work with numbers. We call them arithmetical operations. The word operation comes from the Latin ‘operari’, meaning to work or toil. Of the four arithmetical operations on numbers, addition is the most natural.
Subtraction and addition are inverse operations.
For example, 6 = 4 + 2 is equivalent to 6 − 4 = 2 and also 6 − 2 = 4.
The ability to add numbers in your head is used when you play, or watch sport and when you buy a couple of items at the shops.
Formal or written algorithms are useful when larger numbers make mental calculations difficult. While there are many ways to calculate with arithmetic, the commonly taught algorithms have remained in constant use because they provide an accurate and efficient means to the answer. It is usual for children to develop some basic mental strategies before they are taught formal algorithms.
A student will not develop a number-sense, or fluency with operations, if they move to calculators too quickly. Once an understanding of numbers has been developed, calculators and computers can be used with some confidence that any data-entry errors that are inconsistent with our number sense will be identified. A relatively common example of someone working without a sense of number is the person at the check-out who tries to charge a large sum for an inexpensive item simply because the cash register tells them to, without pausing to think that perhaps the code for the item was incorrect.
The development of solid understanding of addition and subtraction is essential for the development of later concepts including other arithmetical operations, calculations arising from measurements and algebra.
A child can develop the basic ideas related to addition whilst investigating the place value system. However, there are some basic skills that are useful foundations necessary for addition and subtraction of whole numbers:
- Some ability to decompose small numbers into tens and ones.
- Some understanding of place value. (See the module, Counting and Place Value.)
- Counting forwards and backwards by ones and skip-counting.
- The use of the number line to place numbers in relation to other numbers.
- The use of the number line to compare numbers to thirty.
- The ability to make a judgment about the relative size of two or more sets of objects as a pre-cursor to finding the difference between them.
Children’s early experience of addition and subtraction may include an understanding that ‘when I add, I get more’ and ‘when I subtract, I have less than what I started with’. Later, when they have some experience with negative numbers, they will learn that this is not always true.
When we combine two or more disjoint collections of objects, the total number of objects is the sum of the numbers in each of the collections. For example, in the picture below there are 4 pineapples in the first set and 2 pineapples in the second set,

so we say there are 6 pineapples altogether and we can write 4 + 2 = 6.
If we start with 6 pineapples and take away 2, we are left with 4. We can write 6 − 2 = 4.

There is a great deal of language related to the concepts of addition and subtraction.
![]() Addition − and, add, plus, put together with, sum
Addition − and, add, plus, put together with, sum
![]() Subtraction − take away, minus, subtract, difference
Subtraction − take away, minus, subtract, difference
Some of those words are used imprecisely outside of mathematics. For example, there is no exact amount of brown sugar that I need to add to my porridge to make it tasty. It is important that children are exposed to a variety of different terms that apply in addition and subtraction situations and that the terms are used accurately. Often it is desirable to emphasise one term more than others when introducing concepts, however a flexibility with terminology is to be aimed for.
Looking at where words come from gives us some indication of what they mean. The word ‘sum’ comes from the Latin summus and means highest. In Latin, less is written as minus, hence our use of the word to mean subtraction.
Use of the word ‘sum’
It is important that we use the language related to addition correctly. Many years ago students were told to ‘do their sums’ and this could apply to any calculation using any of the four basic operations. This is an inaccurate use of the word ‘sum’. Finding the ‘sum’ of two or more numbers means to add them together. Teachers at this level should take care not to use the word ‘sum’ for anything but addition.
The symbols + and −
The first use of the symbols + and − for addition and subtraction in Europe occurred during the 17th Century. Until then, it was common to use the letter P for plus and the letter M for minus.
Once students are becoming fluent with the concept of addition and subtraction then the symbolic notation, + for addition and − for subtraction, can be introduced. Initially, the ideas will be explored through a conversation, then written in words, followed by a combination of words and numerals and finally using numerals and symbols. At each step, when the child is ready, the use of symbols can reflect the child’s ability to deal with abstract concepts.
The use of the = symbol
It is important that children see the = symbol as a sign for equality. Unfortunately, many children think of = as a ‘put the answer here’ symbol and never develop the ability to think of = as a balance between equivalent statements. One way to avoid this misconception is to present the statement in different ways so
3 + 1 = 
![]() can also be written as
can also be written as  = 3 + 1
= 3 + 1![]() or
or![]() 4 =
4 =  + 1
+ 1
Making connections between equivalent statements is also desirable. As children become familiar with addition and subtraction they may begin to write statements such as
3 + 1 = 2 + 2 since both are equal to 4.
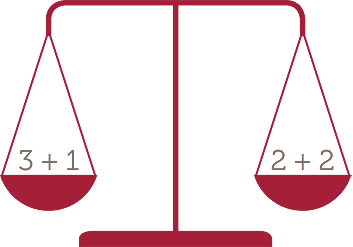 The = symbol can be thought of as a balance in the same way a set of scales balances when the two sides are equivalent. Many teachers use this idea with blocks or other objects of the same size and mass on a set of classroom scales to model addition and subtraction.
The = symbol can be thought of as a balance in the same way a set of scales balances when the two sides are equivalent. Many teachers use this idea with blocks or other objects of the same size and mass on a set of classroom scales to model addition and subtraction.
ADDITION AND SUBTRACTION WITH SINGLE-DIGIT NUMBERS
In the early years of school, a feeling for mathematics is developed through the use of stories, games and conversations accompanied by concrete objects such as toys, pebbles or counters and virtual manipulatives such as interactive whiteboard objects and items that can be moved around on a computer screen. With practice, students will come to visualize objects and manipulate them mentally to assist with calculations. We group all of these types of objects and call them manipulatives.
At this stage, the focus is on the use of numbers up to ten. As the child’s repertoire develops, larger numbers can be introduced. A further development in the child’s understanding will be for these early strategies to become mental strategies.
Much work is sometimes needed with concrete objects before these concepts can be wholly abstracted. As each strategy for carrying out addition and subtraction is developed with the students, there is a similar approach:
The teacher may spend more time on any one of these steps, depending on the needs of the students.
The approach is outlined below for the example 2 + 3 = 5
- Introduce the idea with real-life contexts and concrete objects. There are two girls and three girls sitting at a table in our classroom. How many girls are there altogether? Teacher draws the following or acts out the situation with the students.

- Explain the action in words.
Say: “There are two girls and three girls. There are five girls altogether.”
Write: Two girls and three girls is five girls. - Use numerals instead of number words in a sentence. 2 girls and 3 girls is 5 girls
- Introduce symbols for the action of addition or subtraction. 2 + 3 is 5
- Use the = symbol for equality. 2 + 3 = 5
- Think of other situations to illustrate this problem.
2 girls + 3 girls = 5 girls
2 monkeys + 3 monkeys = 5 monkeys
2 stars + 3 stars = 5 stars
and so on…
One more and one less
Starting with a number that they know, children can be introduced to addition and subtraction through the ideas of ‘one more’ and ‘one less’. These ideas will be familiar to the child who has experienced counting forwards and backwards by ones. Then, we can build the understanding by talking about ‘two more’ and ‘two less’ than a particular number and so on.
In the beginning, these ideas should be discussed in conjunction with the use of collections of concrete objects.
Counters can be used to show addition following the steps as before
 |
 |
||
| Three | One more than three is four | ||
| 3 + 1 is 4 | |||
| 3 + 1 = 4 | |||
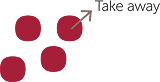
| We can also use counters to demonstrate subtraction. | |||
 |
 |
||
| Four | One less than four is three | ||
| 4 take-away (subtract or minus)1 is 3 | |||
| 4 − 1 is 3 | |||
| 4 − 1 = 3 | |||
‘One more’ can be illustrated on the number line:
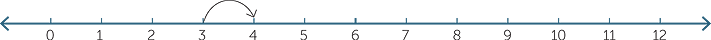
‘One less’ can also be illustrated on the number line:
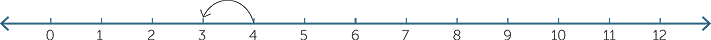
After some time exploring one and two more and one and two less, children begin to recall the addition or subtraction ‘fact’ quickly, without having to think for very long about it. We call this quick or automatic recall of facts, and this comes from understanding the processes involved, not just memorisation.
Addition with single-digit numbers
In their first year of school, before the concepts of addition and subtraction are introduced, children work with small numbers and represent them in different ways, showing their understanding of the number system and the ways we can combine and decompose numbers.
For example, they may use tens-frames with counters to illustrate their understanding that ten is 4 and 6 or 3 and 7 as shown:
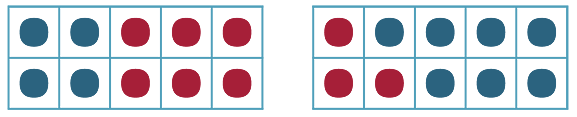
They may demonstrate the different ways to ‘make a number’ using coloured blocks as shown below. In each case, different words have been used to illustrate the variety of vocabulary related to this exercise.
| 7 equals zero add seven |  |
|
| 1 and 6 make 7 |  |
|
| 2 plus 5 is 7 |  |
|
| 7 is 3 plus 4 |  |
|
| four add three is seven |  |
|
| the sum of 5 and 2 is 7 |  |
|
| 6 and one more makes 7 |  |
|
| 7 plus nothing = seven |  |
It is useful for students to become adept at all of the different ways to decompose each number under ten and include these in their repertoire of facts.
For example, 7 = 7 + 0 = 6 + 1 = 5 + 2 = 4 + 3 = 3 + 4 = 2 + 5 = 1 + 6 = 0 + 7
The quick recall of these makes more complex calculations much simpler and efficient later on.
Once the numbers to ten are known, then students can build to twenty and beyond. Knowledge of addition and subtraction with small numbers helps with the more difficult ones. For example, knowing that 6 + 3 is 9 is essential when calculating 26 + 3 = 29.
classroom activity
You will need a beach ball and a permanent marker. Write the numbers 0 to 20 on a beach ball. Pass the beach ball around the class. The teacher describes a procedure or operation to be carried out using the number that lands nearest the right thumb of the person who catches the ball. For example, if a child catches the ball and the number nearest their right thumb is 7. Some suggestions:
 Double the number
Double the number- Say one more than the number
- Tell the class the number that is two less than the number
- Add 6 to the number
- Add 17 to the number
- Tell the class one way to ‘rip apart’ the number
- Say the number needed to make-up to the next ten
Zero
When zero is added to any number, the number is unchanged.
For example,
![]() 5 + 0 = 5 = 0 + 5.
5 + 0 = 5 = 0 + 5.
This is true for all numbers. Hence, we call zero the identity element for addition of
whole numbers.
The identity element for multiplication is 1. When any number is multiplied by 1 the number is unchanged. For example,
![]() 5 × 1 = 5 = 1 × 5
5 × 1 = 5 = 1 × 5
It is important to have this conversation with young children in very simple terms, using lots of examples in the early stages of developing understanding about addition.
Addition on the number line
The number line gives another picture to aid in understanding the addition. Each addition is a jump to the right.
So we can show 4 + 7 = 11 on the number line:

Tens complements
In this module we use the word decompose for the act of breaking a number into smaller parts. In the classroom, teachers might be less formal in their language and use phrases such as ‘pull apart’ and ‘rip apart’ as well as decompose.
Fluency with the different ways to decompose ten is the basis of calculating strategies to come. Since ten is central in our number system, rapid recall of the tens complements is an important skill:
10 = 0 + 10 = 1 + 9 = 2 + 8 = 3 + 7 = 4 + 6 = 5 + 5 = 6 + 4 = 7 + 3 = 8 + 2 = 9 + 1 = 10 + 0
In the early years of schoolling, understanding of the tens complements can be modelled with blocks or counters or shown on the number line.
Use of doubles and near-doubles
Doubles of each of the single-digit numbers can be demonstrated using concrete materials and matching one for one.
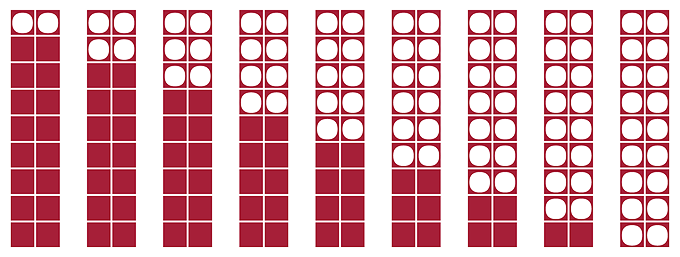
So we get ‘the doubles’
1 + 1 = 2, 2 + 2 = 4, 3 + 3 = 6, 4 + 4 = 8, 5 + 5 = 10, 6 + 6 = 12, 7 + 7 = 14,
8 + 8 = 16, 9 + 9 = 18…
Instant recall of the doubles is a useful skill.
Once the doubles have been mastered the ‘near-doubles’ are the natural next step. For example to calculate 5 + 6 the child might say “I know that 5 + 5 is 10 so 5 + 6 must be 11” and so on.
The doubles can be used in reverse to solve subtractions too. For example, if a child is trying to calculate 12 − 6, they may say “double six is 12, so 12 − 6 must be 6”.
The addition table
It is essential that students can do all the additions in the addition table for two single-digit numbers before they progress to larger numbers. No standard addition algorithm will help students do these additions − they are the building blocks of the addition algorithm.

Fluency with the addition table provides a milestone for understanding for the student and a key stage in the child’s development that the teacher should be aware of. The more automatic these are, the easier the student will find addition and subtraction in the future.
Before moving on to subtraction algorithms, students need to be fluent in all subtractions for which the addition table of single-digit numbers provides the complementary additions. For example, 13 = 8 + 5 gives 13 − 5 = 8 and 13 − 8 = 5.
Once students have grasped addition with single digit numbers and two-digit numbers to around twenty, then they should progress to the larger numbers. A firm understanding of place value is necessary before embarking on this stage of the journey. Many of the strategies for the numbers over 20 build on those used with the small numbers.
Some addition strategies are more useful than others depending on the numbers used. The strategies described earlier for one-digit and two-digit numbers can become mental strategies after much practice. The key to successful and efficient use of mental strategies is to choose the best strategy for the numbers involved. In some cases the best strategy may be the formal algorithm.
Adding single digit numbers
Once the additions to 20 have been mastered, they can be used to solve similar problems where one of the numbers is larger by ten, or a multiple of ten.
For example, if we know that 8 + 7 = 15, then 18 + 7 is ten more, so 18 + 7 = 25
and 28 + 7 = 35 and so on.
Using concrete objects for addition beyond 20
Having a firm understanding of the importance of ‘ten’, and of place-value in general, is necessary before embarking on this stage. To introduce the idea of the ten as a unit, we can make bundles of ten with concrete objects.
Icy-pole sticks bundled into a ten with an elastic band can be used to represent the two numbers to be added.
To add 19 to 12, first we make each number using icy-pole sticks. Bundling each ten with an elastic band.

Then we add the two numbers by pushing the two sets of icy-pole sticks together. We group them into tens and ones,

making new bundles of ten where possible from the loose ‘ones’.
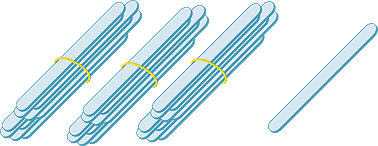
and we find that 19 + 12 is 31.
The next step is to use MAB blocks in the same way, but this time we trade ten ones for one ten in the final step.
Adding a single-digit number to a two-digit number without ‘carrying’
The first step is to understand that this simplifies to the addition of two single-digit numbers. Using hands-on materials is necessary in the early stages. Students then need to mentally apply decomposition and associativity to produce arguments such as the following.
![]() 22 + 5 =(20 + 2) + 5 = 20 + (2 + 5) = 20 + 7 = 27
22 + 5 =(20 + 2) + 5 = 20 + (2 + 5) = 20 + 7 = 27
This is decomposition followed by the use of the associative rule.
When children are using the number line, we can identify which children are still counting on by ones

from those that are skip-counting by fives.

Adding a single-digit number to a two-digit number with carrying
Once the previous case is mastered, students should be progressed to the extra complication of the need to go over the ten or to ‘carry’ a ten. In the first instance, students would use tens complements as illustrated below.
28 + 5 = 28 + 2 + 3 = 30 + 3 = 33
On the number line, this corresponds to jumping to the first number, then jumping to the nearest ten above it, then jumping the rest of the way. The mental strategy essentially involves calculating the size of this last jump.

Alternative strategies should also be investigated. Different strategies should be recognized as equally valid and their relative merits discussed. In particular, students should be introduced to the process used in the standard algorithm in an informal way. For example,
![]() 28 + 5 = 20 + 8 + 5 = 20 + 13 = 33
28 + 5 = 20 + 8 + 5 = 20 + 13 = 33
We observe that this argument reduces to a decomposition and two applications of adding two single-digit numbers, with one of the additions taking place in the tens column.
Adding two two-digit numbers with no carrying involved
Mental strategies for adding two-digit numbers usually involve decomposing one of them and reducing the problem to one, or a combination, of the cases already discussed. We illustrate this with the example 24 + 15.
First add ones then add tens.
This approach corresponds to
![]() 24 + 15 = (24 +5) + 10 = 29 + 10 = 39
24 + 15 = (24 +5) + 10 = 29 + 10 = 39
This is the approach that is formalised in the standard algorithm. On the number line, this corresponds to skip-counting as illustrated below.

First add tens then add ones.
This involves the calculation
![]() 24 + 15 = 24 + 10 + 5 = 34 + 5 = 39
24 + 15 = 24 + 10 + 5 = 34 + 5 = 39
This is a valid approach. Indeed, developmentally it often comes before the previous technique. It is messier when applied algorithmically, so it is important that students who naturally discover this method also understand the previous approach.
On the number line this corresponds to implementing the second and third jumps above in the opposite order.

Adding two two-digit numbers with carrying involved
The next level of complication involves introducing ‘carries’. We illustrate various techniques using 28 + 15.
First add ones then add tens
![]() 28 + 15 = 28 + 5 + 10 = 33 + 10 = 43
28 + 15 = 28 + 5 + 10 = 33 + 10 = 43
First add tens then add ones
![]() 28 + 15 = 28 + 10 + 5 = 38 + 5 = 43
28 + 15 = 28 + 10 + 5 = 38 + 5 = 43
This technique requires revisiting the tens after the ones have been dealt with.
Build to tens
In this technique we decompose one number to create a tens complement for the other. This can usually be done in more than one way. For example
![]() 28 + 15 = 28 + 2 + 13 = 30 + 13 = 43 and 28 + 15 = 23 + 5 + 15 = 23 + 20 = 43.
28 + 15 = 28 + 2 + 13 = 30 + 13 = 43 and 28 + 15 = 23 + 5 + 15 = 23 + 20 = 43.
Our choice of approach for subtraction depends on the numbers involved. We usually calculate 20 − 17 using complementary addition, whereas we calculate 20 − 3 directly by taking away. Both correspond to the same addition fact 20 = 17 + 3.
Once students start using an algorithm, they might be less likely to develop new strategies. It is therefore important that students are given the opportunity to develop a variety of useful strategies before an algorithm is introduced.
Subtraction as take-away
Subtraction can be thought of as removing some objects from a set of objects.
If we start with 9 keys

And take away 7

We are left with 2 keys

This can be shown on the number line. A subtraction can be thought of as a jump to the left on the number line.
So, for 9 − 7 = 2, we start at the number nine, and take a jump of 7 to the left.

9 − 7 = 2
Subtraction as difference
There is another way to think about subtraction, as the difference between the size of two collections. This helps us answer questions of the type “What is the difference between 9 and 7?” This can be shown using counters.
We line up 9 counters and then line up 7 counters, placing them so that there is one-to-one correspondence between the collections as far as possible:

and we can see that there is a difference of 2 in the size of the collections. So we say that the difference between 9 and 7 is 2.
Difference arises naturally when comparing the heights of two people.
For example, Harry is 123cm tall and Ally is 112cm tall. How much taller is Harry than Ally? We calculate the difference between Harry’s height and Ally’s height and conclude that Harry is 11 cm taller than Ally or Ally is 11cm shorter than Harry.
Subtracting as “adding on”
Sometimes we add to solve subtraction situations. To calculate the subtraction 5 − 2 we can ask “What do you add to 2 in order to get to 5?” This can also be illustrated on the number line.
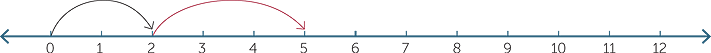
That is 5 − 2 = 3
One example of this is “I have 5 pencils and my brother has 2, so I have 3 more pencils than my brother”.
Once students have grasped subtraction with single digit numbers and two-digit numbers to around twenty, then they should progress to the larger numbers. It is at this point that the student will need a firm understanding of place value. Many of the strategies for the numbers over 20 build on those used with the small numbers.
Using concrete objects for subtraction beyond 20
When we explored the use of concrete objects for addition beyond 20, we used icy-pole sticks and explained that the next step would be to use MAB Blocks. In this section, we will use MAB blocks and allow the reader to determine how the icy-pole sticks might be used as the introductory step for subtraction.
Subtraction without trading
For example, to subtract 34 from 76 we make the number 76 using 7 tens and 6 ones with MAB

then take-away 4 ones and 3 tens, which leaves 42.

Subtraction with trading
Trading, or decomposition, relies on the student understanding that ten ones can be traded for one ten.
To calculate 76 − 39, we make the number 76 using 7 tens and 6 ones with MAB.

The next step is to take 9 ones. To have enough ones we need to ‘trade’ one ten for ten ones:
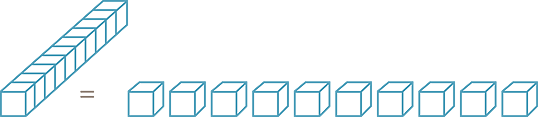
making 6 tens and 16 ones

Now we can take 9 ones and 3 tens, which results in
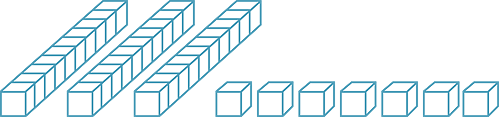
the calculation 76 − 39 = 37.
The trading is an important step.
| 76 − 39 | ||
| = | 60 + 16 − (30 + 9) | |
| = | 60 − 30 + 16 − 9 | |
| = | 30 + 7 | |
| = | 37 |
Single-digit subtraction with no change to ‘columns’
When a student sees 68 − 5, they must recognize that the mental calculation is not much more complicated than 8 − 5 and conclude that 68 − 5 = 63. In doing so, they are mentally decomposing 68 and calculating
![]() 68 − 5 = 60 + (8 − 5) = 63
68 − 5 = 60 + (8 − 5) = 63
Decomposition is a basic component of all subtraction algorithms.
Single digit subtraction with change to ‘columns’
Students should be asked to consider calculations such as 62 − 5 = 57 and encouraged to perform the subtraction in different ways including:
- Counting backwards and keeping track of the steps.
For example,
- Breaking the number apart into manageable steps.
For example, 62 − 5 = 60 − 3 = 57
- Mentally trading one ten for ten ones.
For example, 62 − 5 = 50 + 12 − 5 = 57
Subtraction by equal addition
The principle of equal addition is the observation that if you add the same amount to two numbers, their difference does not change.
In the example,
![]() 37 − 18 = 39 − 20 = 19,
37 − 18 = 39 − 20 = 19,
we have added 2 to both 37 and 18 to make the calculation easier.
Note that the principle of equal addition also tells us that if you subtract the same amount from two numbers their difference does not change. This can be used in a mental subtraction such as
![]() 115 − 65 = 100 − 50 = 50
115 − 65 = 100 − 50 = 50![]() or
or![]() 115 − 65 = 110 − 60 = 50.
115 − 65 = 110 − 60 = 50.
THE RELATIONSHIP BETWEEN SUBTRACTION AND ADDITION
Each addition statement gives two subtraction statements.
For example, 4 + 6 = 10 gives 10 − 4 = 6 and 10 − 6 = 4.
As children build understanding about addition and subtraction, it is important that they become accustomed to making these connections.
We can use addition to solve subtraction problems because subtraction is the inverse operation to addition. To “undo” an addition we perform the corresponding subtraction and vice-versa. This relationship makes it tempting to assume subtraction behaves in a similar way to addition, but this assumption is incorrect and this thinking can be the source of many errors in arithmetic.
Addition satisfies the following important properties.
The any-order property for addition states that a list of whole numbers can be added two at a time in any order to give the same result.
The any-order property of addition is a consequence of two properties.
Addition is commutative, in the sense that a + b = b + a for all numbers a and b.
For example, 14 + 6 = 6 + 14
Addition is associative, in the sense that (a + b) + c = a + (b + c) for all numbers,
b, and c.
For example, (3 + 2) + 6 = 3 + (2 + 6)
Subtraction is not as well-behaved as addition.
Subtraction is not commutative. For example, 2 − 4 ≠ 4 − 2.
Subtraction is not associative. For example, 6 − (4 − 1) ≠ (6 − 4) − 1.
In particular, the any-order property of addition does not transfer to subtraction. With subtraction, the order in which operations are performed is critical. Failing to observe and understand this can cause many arithmetic errors.
classroom activity
Write the following numbers on the board (or choose some of your own):
![]() 16
16![]() 29
29![]() 4
4![]() 13
13![]() 42
42![]() 10
10![]() 19
19![]() 23
23![]() 17
17![]() 30
30![]() 6
6![]() 46
46![]()
Ask students to select two or three numbers and show a connection between them using + for addition or − for subtraction and = for equality and any of the strategies the students know for addition or subtraction.
For example,
- Double 23 is 46, so 23 + 23 = 46
- 23 + 6 = 29, so 29 − 23 = 6 and 29 − 6 = 23
An algorithm works most efficiently if it uses a small number of strategies that apply in all situations. So algorithms do not resort to techniques, such as the use of near-doubles, that are efficient for a few cases but not useful in the majority of cases. The benefit of an algorithm is that it can become an automated process that, once understood, provides an accurate and efficient means to finding a solution. Algorithms are dependable and efficient tools in mathematics.
Algorithms for addition and subtraction should not be introduced until students have started to develop a familiarity with basic addition and subtraction to twenty.
Most addition and subtraction algorithms rely on place value for their implementation. Thus the ability to line up numbers in their place value columns is a pre-cursor to the introduction of both the addition and subtraction algorithms.
the standard addition algorithm
As a procedure, the standard algorithm for addition works in the following steps.
- Align the digits in the numbers into columns of corresponding place value.
- Draw a line under the last number you are adding and put a + somewhere to note which operation you are performing.
- Starting from the rightmost column and working from right to left, perform the following subprocedure for each column.
- Add the digits in the column, including any carry digits.
- Write the units digit of your answer in the same column, but under the line.
- Make a note of any carry digits in the next column to the left.
If we want to add 39 to 45 we can use the addition algorithm.
|
|
|
|
|
|
We say, ‘9 ones plus 5 ones is 14 ones’. 14 ones is the same as 1 ten and 4 ones. Write 4 in the ones column and carry 1 ten |
|
|
|
Now look at the tens column. We say, ‘3 tens + 4 tens + 1 tens Write the 8 in the tens column. |
The addition algorithm can be extended to add any number of numbers of any size. All you need to do is add the columns from right to left, and carry whenever you get ten or more.
The digits are aligned in columns to ensure that like terms are added. The digits in smaller fonts are the carry digits and are reminders to add values into that column generated from the sum of the digits in the previous (that is, immediately to the right) column. In the standard algorithm, the location of the carry digits are habitual, as is the location of the + sign.
Misaligned columns
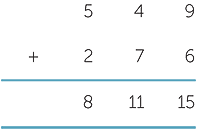
A common early error is to misalign the columns. For example, miscalculating 278 + 54 by writing

Entering a two-digit number into a single column
Another common error is to enter a two-digit number into a single column, thereby destroying the place-value alignment in the solution. For example,
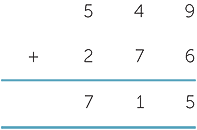
Forgetting to add the carry digits in the calculation
For example,
Adding several numbers together
When we use the standard algorithm to add several numbers together, new situations arise.
Adding within columns
When implementing the algorithm to add two numbers, the most complicated process we face when adding a column of digits is the sum of two single-digit numbers. When we use the algorithm to add more than two numbers, we may have to use mental arithmetic to add a single-digit number to a two-digit number. Consider the following example.

When adding the digits in the ones column we calculate 3 + 9 = 12 and then 12 + 6 = 18. Similarly, when adding the digits in the tens column we also need to use mental arithmetic to add a single-digit number to a two-digit number.
Higher carry digits
In some cases, the carry digits are greater than 1.
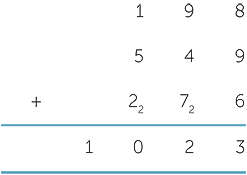
When we add a long list of numbers, the sum of a column may be a three-digit number. In this case we will need to add a single-digit number to a three-digit number, and the carry will be a two-digit number.
STANDARD SUBTRACTION ALGORITHMS
We need an algorithm for subtraction, just as we have an algorithm for addition. Algorithms must be robust − that is, they must be easy to remember and implement.
The special case
When each digit in the ‘bottom number’ is less than or equal to the digit in the ‘top number’, you simply subtract in each column.

The general case
We need to deal with subtractions such as
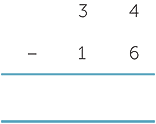
where the 6 is greater than the 4. There are several standard approaches to this, and we discuss the two most common.
The equal addition method (also known as ‘borrow and pay back’)
This method is based on the observation that adding 10 to both numbers does not change the difference between them. So we write
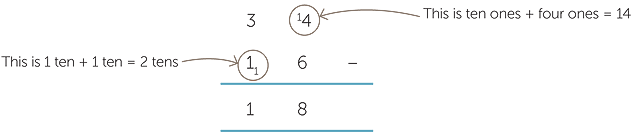
to mean that we add ten ones to 34 and one ten to 16. The algorithm works because, arithmetically, we are actually subtracting 26 from 44. The difference between 44 and 26 is the same as the difference between 34 and 16.
This can be seen on the number line:
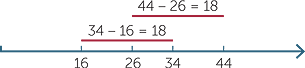
CLASSROOM ACTIVITY
Demonstrate 42 − 17 = 45 − 20 = 25 on the number line.
- Draw an accurate number line on the board, marking in benchmarks such as 0, 50, the multiples of ten and the numbers 42 and 17.
- Cut a streamer equal to the distance on the number line between 42 and 17.
- Slide the streamer along the number line to show that this is equal to 45 − 20 and to the distance between 0 and 25
In the subtraction below, we are adding ‘ten tens’ to the top line and adding one hundred to the bottom line.

If there are many zeroes, we may need to perform equal addition in several columns before we can complete the calculation, as illustrated below.

You can check that 3004 = 46 + 2958.
The traditional terminology for equal addition, “borrow and pay back”, is an unfortunate term because it does not accurately describe the process. The phrase “add the same to both numbers” is a more accurate description of the equal addition principle.
Decomposition method (also known as ‘trading’)
The names trading and decomposition come from the place-value representation of the numbers, as modelled by Diene’s blocks (MAB). The subtraction of one from the tens column and adding ten to the ones column can be viewed as the “long” block being traded for, or decomposed into, ten “ones”.
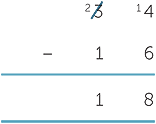
We calculate 34 − 16 by writing 34 as 20 + 14 instead of 30 + 4.
|
34 − 16 |
= (20 + 14) − (10 + 6) |
|
|
= (20 − 10) + (14 − 6) |
||
|
= 10 + 8 |
Algorithmically, we indicate the new regrouping as a conversion of one ten into ten ones.
Cascading trades
Consider the following calculation

This can get messy using the decomposition method if you don’t have a good number sense. We could implement the calculation one column at a time, but this is time consuming and can get untidy and hard to follow.

People often say `I haven’t got any tens’. But in fact they have 300 tens! The key is to think of the 3000 as 300 tens and shift one of the tens over to the ones column, leaving you with 299 tens.
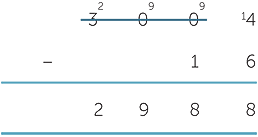
This way the calculation looks clean and is fast.
The advantages and disadvantages of the equal addition
and decomposition algorithms
An advantage of the equal addition method is that it is easier to use and produces a tidier and less cluttered layout. A disadvantage of the method is that the mathematics underpinning the technique has an extra layer of complexity.
An advantage of the decomposition method is that it is initially easier to explain, especially using place-value blocks. The algorithm depends on expressing one number in a more convenient format. A disadvantage is that the layout can get messy, mainly because of all of the markings, and this can lead to more errors.
CLASSROOM ACTIVITY
Calculate 842 − 678 using equal addition and using decomposition (trading) to compare the two techniques.
Understanding addition and subtraction of whole numbers is essential for the further study of arithmetic and mathematics. Multiplication of whole numbers can be thought of as repeated addition. Fluency with subtraction is essential for division. Subtraction is used when we perform division calculations, especially with the use of the division algorithm.
A strong number-sense is an invaluable advantage in the understanding of algebra. In particular, the process of decomposing and recombining numbers aids the understanding of general algebraic manipulations. A strong grounding in arithmetic sets a student up for success in algebra.
Consumer arithmetic contains a wealth of applications of addition and subtraction. These include basic calculations, such as finding the change in a financial transaction, to calculating discounts and mortgage repayments.
Addition, in the sense of measuring the size of combined sets, was probably done as soon as people counted. Addition itself does not change; 4 + 2 is six regardless of whether you write it as 6, VI or 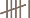 . Just as the history of number is really all about the development of numerals, the history of addition and subtraction is mainly the history of the processes people have used to perform calculations. The development of addition and subtraction are not documented because they are essentially prehistoric. The oldest written records of mathematical calculations date back over 4000 years to the ancient Egyptians and Babylonians. These documents include addition and subtraction problems, so we know that these operations were already used by then.
. Just as the history of number is really all about the development of numerals, the history of addition and subtraction is mainly the history of the processes people have used to perform calculations. The development of addition and subtraction are not documented because they are essentially prehistoric. The oldest written records of mathematical calculations date back over 4000 years to the ancient Egyptians and Babylonians. These documents include addition and subtraction problems, so we know that these operations were already used by then.
The development of the Hindu-Arabic place-value notation enabled the implementation of efficient algorithms for arithmetic and was probably the main reason for the popularity and fast adoption of the notation.
The word algorithm is derived from the name of Muhammad al-Khwārizmī, an Islamic astronomer and mathematician. In 825 AD he wrote a treatise entitled Book on Addition and Subtraction after the Method of the Indians. It was translated into Latin in the 12th century as Algoritmi de Numero Indorum. The term Algoritmi probably referred to
al-Khwarizmi rather than a general procedure of calculation, but the name has stuck.
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()




