The Cartesian plane

The general case

We can obtain a formula for the length of any interval. Suppose that \(P(x_1,y_1)\) and \(Q(x_2,y_2)\) are two points.

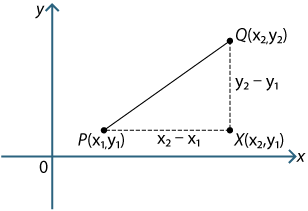
Form the right-angled triangle PQX, where X is the point \((x_2,y_1)\),

\(PX = x_2 − x_1\) or \(x_1 − x_2\) and \(QX = y_2 − y_1\) or \(y_1 − y_2\)

depending on the positions of \(P\) and \(Q\).

By Pythagoras' theorem:

\(PQ^2\)	\(=PX^2+QX^2\)
	\(=(x_2-x_1)^2+(y_2-y_1)^2\)

Therefore \(PQ = QP =\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)

Note that \((x_2-x_1)^2\) is the same as (\(x_1-x_2)^2\). Therefore it doesn't matter whether we go from \(P\) to \(Q\) or from \(Q\) to \(P\). The result is the same.

Distance between two points

Some other questions