The Cartesian plane

Question 1

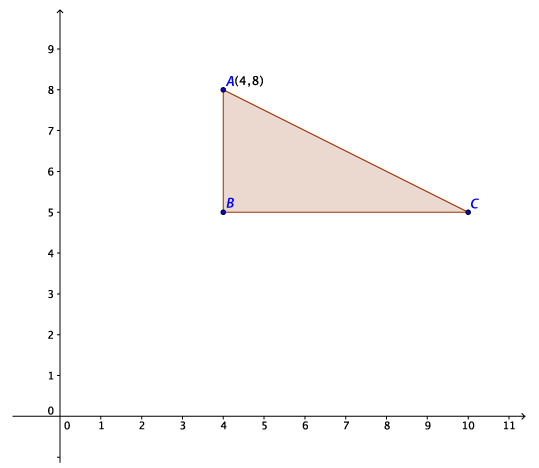
Right-angled triangle ABC with right angle at B on Cartesian plane. A above B marked with coordinates (4, 8). C is to the right of B.
The coordinates of point A are (4, 8).

AB is parallel to the y-axis and angle ABC is a right angle.
If AB = 3 and BC = 6, what are the coordinates of point C?

Solution

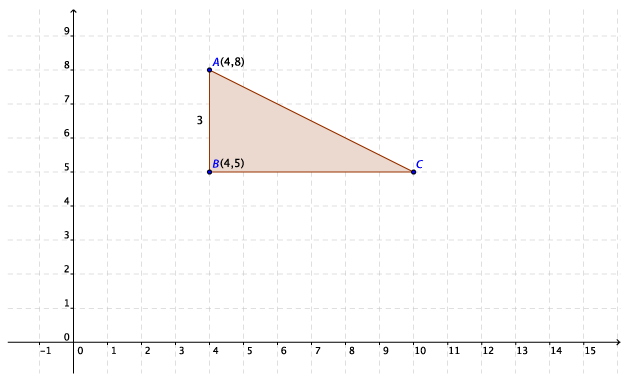
Right-angled triangle ABC with right angle at B on Cartesian plane. A above B marked with coordinates (4, 8). C is to the right of B. Coordinates of B (4, 5). Length AB = 3.

The coordinates of the point A are (4, 8).
The line segment (interval) AB is parallel to the y–axis and so the point B has x–coordinate 4.
The length of AB is 3 units.
So, the coordinates of B are (4, 5).
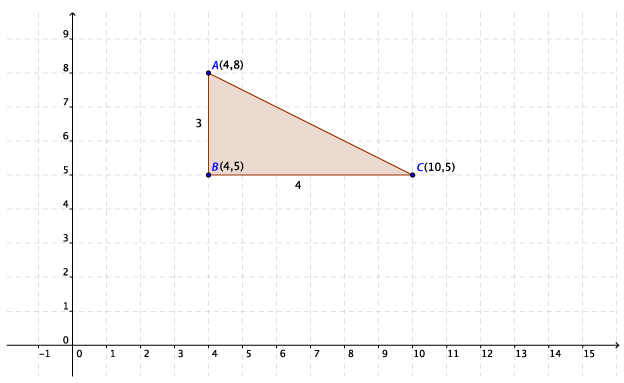
The line segment BC is parallel to the x–axis.
So, the y–coordinate of point C is also 5.
The length of BC is 6.
The coordinates of point C are (10, 5).

Right-angled triangle ABC with right angle at B on Cartesian plane. A above B marked with coordinates (4, 8). A with coordinates (4, 5) and C (10, 5)

Distance between two points

© Australian Mathematical Sciences Institute, except where indicated otherwise. This material is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported (CC BY-NC 3.0) licence http://creativecommons.org/licenses/by-nc/3.0/