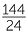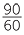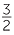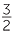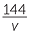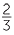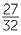The Improving Mathematics Education in Schools (TIMES) Project
- Fluency with the arithmetic of whole numbers and fractions.
- Familiarity with the basic units of distance, time, mass and volume.
- Sketching straight line graphs.
- Determining the gradient of a straight line graph.
- Familiarity with ratios and rates.
- Simple formulas and equations.
Doctors and nurses calculate how much of a medicine is to be administered by using
the ideas of proportion. For example, suppose that a medicine is to be administered at
20 micrograms per kg per min. If the patient weighs 56 kg, how many milligrams should the patient receive in one hour?
People working in science, finance and many other areas look for relationships between various quantities of interest. These relationships often turn out to be either linear or hyperbolic. That is, the graph relating these quantities is either a straight line or a hyperbola.
In this module we are mainly concerned with formulas (see the module, Formulas) for which the associated graphs are either straight lines or rectangular hyperbolas. In the first case we have direct proportion and in the second case inverse proportion.
To take a very simple example: I = 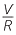 is Ohm’s law, relating V the voltage (potential difference), I the current and R the resistance of the conductor.
is Ohm’s law, relating V the voltage (potential difference), I the current and R the resistance of the conductor.
Ohm’s law is fundamental in the study of electricity. If R is a constant, I is directly proportional to V. If V is a constant, I is inversely proportional to R. In the module, Rates and Ratios, the formula d = vt connecting distance travelled d, time taken t and speed V was introduced and discussed. For a constant speed, the distance travelled is proportional to time travelled and for a fixed distance, the time taken is inversely proportional to the speed.
More complicated situations are also considered using proportion. A familiar example from science is that for a body moving with constant acceleration the distance travelled
is proportional to the square of the time travelling.
There are a huge variety of applications of proportion and this will become evident through the many examples given in the content section of the module.
A number of formulas from physics will be introduced in this module, however a knowledge of the associated physical principles is not a necessity for the reader.
In this module we will use the words ‘variable’ and ‘constant’ instead of the one
word ‘pronumeral’.
Definition
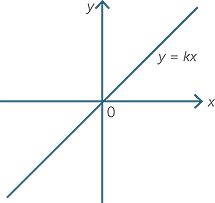
The variable y is said to be directly proportional to x if
![]() y = kx for some non-zero constant k.
y = kx for some non-zero constant k.
The constant k is called the constant of proportionality.
The statement, ‘y is directly proportional to x’, is written symbolically as
![]() y
y  x.
x.
 Sometimes in the literature the word variation is used instead of proportion.
Sometimes in the literature the word variation is used instead of proportion.
The graph of y = kx is a straight line passing through the origin. Its gradient k is the constant of proportionality. (The values that x can take are often the positive real numbers, but this is not always the case.)
Here is a simple example of direct proportion.
David drives from his home at a constant speed of 100km/h.
The formula for the distance d km travelled in t hours is
![]() d = 100t.
d = 100t.
David will go twice as far in twice the time, three times as far in three times the time and so on.
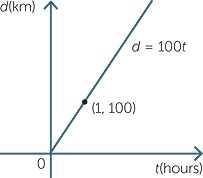
The graph of d against t is a straight line passing through the origin. In this example d is directly proportional to t and we write d  t. The constant 100 is the constant of proportionality and this is the gradient of the line.
t. The constant 100 is the constant of proportionality and this is the gradient of the line.
Notice that in this example the constant of proportionality is the speed, that is, a rate. Rates are one of the most common examples of proportion.
Rates and ratios have been considered in the module, Rates and Ratios. The ideas in
that module are further developed here and considered from a different perspective.
Rates
All constant rate situations, similar to the above example of the car travelling at constant speed, provide examples of direct proportion.
For example, if water is flowing into a tank at the rate of 5 litres/min, the amount of water V litres that has flowed into the tank after t minutes is given by the formula V = 5t. Thus the volume of water is directly proportional to the time that the water is flowing into it.
Here is a table of values for this situation.
| t | 1 | 2 | 3 | 4 |
| V | 5 | 10 | 15 | 20 |
We can see from the table that 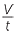 is a constant.
is a constant.
![]()
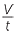 =
= 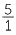 =
= 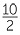 =
= 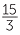 =
= 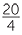 = 5.
= 5.
Thus the ratio V : t is constant.
![]() V : t = 5 : 1 = 10 : 2 = 15 : 3 = 20 : 4.
V : t = 5 : 1 = 10 : 2 = 15 : 3 = 20 : 4.
We can see from this example how constant rates, constant ratios and direct proportion are related.
Ratios
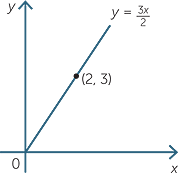
Suppose that the dimensions of a rectangle are in the ratio 3 : 2. Let x be the length of the rectangle and y the width. Then
![]() y : x = 3 : 2 or
y : x = 3 : 2 or 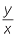 =
= 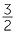 or y =
or y = 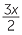 .
.
The width y of the rectangle is directly proportional to the length of the rectangle.
The constant of proportionality is 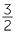 . The graph of y against x is a straight line through
. The graph of y against x is a straight line through
the origin with gradient 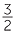 .
.
EXAMPLE
A ribbon has width 3cm and a length lcm is cut off. The area Acm2 of the ribbon cut off is given by the formula A = 3l. Write a proportion statement in words and in symbols, state the constant of proportionality and sketch the graph of A against l.
Solution
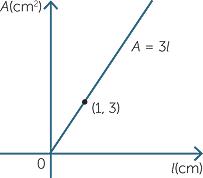 Since A = 3l, A is directly proportional
Since A = 3l, A is directly proportional
to l and we can write A  l. The constant
l. The constant
of proportionality is 3.
Properties of direct proportion
The following are three important properties of proportion.
| Property 1 | x  x x |
(Reflexivity) |
| Property 2 | If y  x then x x then x  y y |
(Symmetry) |
| Property 3 | If y  x and x x and x  z then y z then y  z z |
(Transitivity) |
| Proof of property 1 | x = 1 × x. The constant of proportionality is 1. | |
| Proof of property 2 | y  x, there is a non-zero constant such that y = kx. x, there is a non-zero constant such that y = kx. |
|
Hence x = 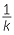 y, so x y, so x  y with constant of proportionality y with constant of proportionality 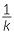 . . |
||
| Proof of property 3 | y  x, there is a non-zero constant k1 such that y = k1x. x, there is a non-zero constant k1 such that y = k1x. |
|
x  z, there is a non-zero constant k2 such that x = k2z. z, there is a non-zero constant k2 such that x = k2z. |
||
Hence y = k1k2z, so y  z with constant of proportionality k1k2. z with constant of proportionality k1k2. |
||
There are many applications that illustrate the second and third properties
of direct proportion.
Example of property 2
If a car is travelling at 60km/h the distance Skm travelled in t hours is given by
S = 60t. Here S  t and the constant of proportionality is 60. Rearranging gives
t and the constant of proportionality is 60. Rearranging gives
t = 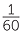 S. Hence t
S. Hence t  S and the constant of proportionality is
S and the constant of proportionality is 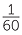 .
.
Example of property 3
A rice crop requires 40kg per hectare of a nitrogen nutrient fertilizer and the cost per kg
is 50¢. Let A hectares be the area, n be the number of kilograms of fertilizer required, and
$C be the total cost of fertilizer. We have n = 40A and C = 0.5n. This means n  A and
A and
C  n. Hence C
n. Hence C  A. We can see that C = 20A, so C
A. We can see that C = 20A, so C  A.
A.
Further examples of direct proportion
There are many examples of direct proportion. Here are some elementary examples to show how ubiquitous this idea is.
From commerce
- When we read an oil price of $72 a barrel we are assuming that the price of a quantity of oil is directly proportional to the number of barrels. Most cost per unit problems involve direct proportion.
- The amount of GST payable on an item is directly proportional to the cost of the item. The constant of proportionality is 10%.
- For a given interest rate, for example 6% per annum, the amount of interest earned over a fixed period is directly proportional to the amount invested.
- Exchange rates. The cost of an item in euros is proportional to its cost in dollars.
From measurement
- Conversions between units usually involves direct proportion. For example converting centimetres to metres or feet to metres. There are examples where conversion of units does not involve direct proportion, such as converting Fahrenheit to Centigrade.
- The depth of water in a container that is a right prism with its ‘base’ horizontal is directly proportional to the volume of water, and the volume is directly proportional to the depth of the water
- The perimeter of a regular polygon is directly proportional to the length of one side.
- The circumference of a circle is directly proportional to the radius of the circle with constant of proportionality 2π. Conversely, the radius of a circle is directly proportional to the circumference of the circle. (C = 2πr and r =
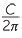 )
) - On a map drawn to scale, the distance between any two points on the map is proportional to the distance between the two locations that the points represent,
with the constant of proportionality being the scale of the map.
From science
- The mass of a body is proportional to its volume. The constant of proportionality is
the density of the body. For example, the density of water is 1 gram/cm3. (The formula is m = ρV) - The acceleration of a body is proportional to the resultant force acting on it.
The constant of proportionality is the mass. (The formula is a =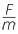 )
) - The force acting on a certain object due to gravity is proportional to the object's mass. The constant of proportionality between the mass and the force is known as gravitational acceleration.
- For a constant force acting on a body, the work done by the force is proportional to the distance through which the body moves. (The formula is W = Fd)
- The gravitational potential energy of a body above the earth’s surface is proportional to the height of the body above the earth’s surface. The proportionality constant is the product of the mass and gravitational acceleration.
- For a body moving in a circle with constant angular speed, the linear speed (tangential speed) is proportional to the angular speed. The constant of proportionality is the radius of the circle. (The formula is v = ωr)
- Archimedes’ principle: The weight of the displaced fluid is directly proportional to the volume of the displaced fluid. In simple terms, the principle states that the buoyancy force on an object is equal to the weight of the fluid displaced by the object.
- Charles’ law: At constant pressure, the volume V of a given mass of an ideal gas increases or decreases by the same factor as its temperature T on the absolute temperature scale (i.e. the gas expands as the temperature increases).
The properties of direct proportion can be usefully applied in each of the examples above. Here are two other important examples.
Currency exchanges (an example of property 2): Convert Australian dollars to United States dollars and United States dollars to Australian dollars. (The reciprocal of the proportionality constant used for the first conversion is applied for the second.)
Unit conversions (an example of property 3): Change metres to millimeters by first changing metres to centimetres and then changing centimeters to millimetres.
EXERCISE 1
The medical example which begins the motivation section also uses property 3.
Medicine is to be administered to a patient at 20 micrograms/kg/min. If the patient weighs 56kg, how many milligrams should the patient receive in one hour?
EXERCISE 2
In 2008 during the global financial crisis one Australian dollar was worth 0.618 United States dollars. How much was one United States dollar worth in Australian dollars?
(Think about the golden ratio after completing this.)
Finding the constant of proportionality
If y is proportional to x, the proportionality constant can be found if just one value of x and the corresponding value of y are given.
EXAMPLE
The variable y is proportional to the variable x. When x = 4, y = 11. Find the proportionality constant, and hence write the formula for y in terms of x.
Solution
Since y is proportional to x, there is a constant k such that y = kx.
When x = 4, y = 11, so 11 = 4k and k = 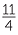 .
.
Hence y = 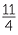 x.
x.
The procedure for solving this question was as follows.
- Write the proportion statement as an equation involving a constant k.
- Use the information in the question to find the value of k.
- Rewrite the formula with the calculated value of k.
Proportionality to a square or a cube
A metal ball is dropped from the top of a tall building, and the distance it falls is recorded each second.
From physics, the formula for the distance d m that the ball has fallen in t seconds is
![]() d = 4.9t2.
d = 4.9t2.
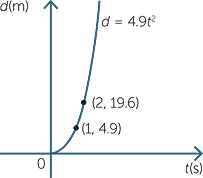 In this case, we say that d is directly proportional
In this case, we say that d is directly proportional
to the square of t. When we plot the graph of d
against t the graph is half the parabola.
But what happened to our straight line through the origin which we expect from direct proportion? We can obtain a straight line by plotting d against t2 rather than against t.
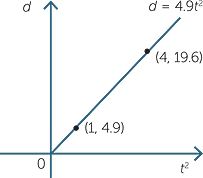
| t | 0 | 1 | 2 | 3 |
| t2 | 0 | 1 | 4 | 9 |
| d | 0 | 4.9 | 19.6 | 44.1 |
The gradient of this line is 4.9.
This is now a straight line passing through the origin, with gradient 4.9.
We can see that d is proportional to t2, and we write this as d  t2.
t2.
This means that for any two values t1 and t2 with corresponding values d1 and d2,
![]()
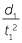 =
= 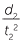 = 4.9.
= 4.9.
So once again the ratio is a constant and the gradient of the line is the constant of proportionality.
There are many examples where one quantity is proportional to the square
or cube of another. Here are some other elementary examples:
- The area of a circle is directly proportional to the square of its radius.
(The formula is A = πr2) - The volume of a sphere is directly proportional to the cube of its radius.
(The formula is V =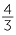 πr3)
πr3) - The period of a simple pendulum is directly proportional to the square root of its length. (This is an approximation for small arcs of oscillation.) We note that if y

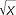
then x y2.
y2. - The volume of a square-based prism of constant height is proportional to the
square of the length of a side of the base. - The kinetic energy of a body is proportional to the square of its speed.
(The formula is E =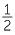 mv2)
mv2)
As we have seen above, to find the constant of proportionality just one pair of values
is needed.
EXAMPLE
From physics, it is known that the energy E μJ (this is the abbreviation for microjoules) of an object in motion is directly proportional to the square of its speed V m/s. If an object travelling at a speed of 10 m/s has energy 400 μJ, find:
a![]() the constant of proportionality.
the constant of proportionality.
b![]() the formula for E in terms of v.
the formula for E in terms of v.
c![]() the energy of an object travelling at a speed of 15 m/s.
the energy of an object travelling at a speed of 15 m/s.
d![]() the speed if the moving object has energy 500 μJ.
the speed if the moving object has energy 500 μJ.
Solution
| a | The energy of the object is directly proportional to the square of its speed. | |||
| That is | E | = kv2, for some constant k. | ||
| Now | E | = 400 when V = 10, | ||
| so | 400 | = 100k | ||
| k | = 4. | |||
| b | From part a | E | = 4v2. | |
| c | When V = 15 |
|||
| E | = 4 × 152 | |||
| = 900, so its energy is 900 μJ. | ||||
| d | When E = 500, | 500 | = 4 × v2 | ||
| v2 | = 125 | ||||
| v | = |
||||
| = 5 |
EXAMPLE
The mass, m grams of a plastic material required to mould a solid ball is directly proportional to the cube of the radius r cm of the ball. If 40 grams of plastic is needed
to make a ball of radius 2.5 cm, what size ball can be made from 200 grams of the same type of plastic?
Solution
We know that m = kr3, where k is a constant and
| m = 40 when r = 2.5 | ||
| Thus | 40 = k × (2.5)3 | |
| k = 2.56. |
So the formula is m = 2.56r3
| When m = 200, | 200 = 2.56r3 |
| r3 = 78.125 | |
| r = |
|
| r ≈ 4.27 cm |
EXERCISE 3
The power p kW needed to run a boat varies as the cube of its speed s m/s. If 400 kW will run a boat at 3 m/s, what power is needed to run the same boat at 5 m/s?
If one quantity is proportional to another, we can work out what happens to one of the quantities when the other is changed.
Let y = kx for a positive constant k.
If the value of x is doubled, then the value of y is doubled. The best way to demonstrate this is to substitute a particular value of x.
For example if we substitute x = 7 then y = 7k and when x = 14 gives y = 14k.
Similarly, if the value of x is tripled then the value of y is tripled. We can use this with any proportion question.
EXAMPLE
Given that a  b3, what is the change in a when b is
b3, what is the change in a when b is
a![]() doubled
doubled ![]() b
b![]() halved?
halved?
Solution
Since a  b3, a = kb3 for some positive constant k.
b3, a = kb3 for some positive constant k.
| a | To see the effect of doubling b, choose b = 1. Any value can be chosen but b = 1 is the easiest to deal with. | ||
| When b = 1, | a = k | ||
| When b = 2, | a = 8k | ||
| When b is doubled, a is multiplied by 8. | |||
| b | When b = 1, | a = k | |
When b = 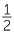 |
a = 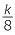 |
||
| When b is halved, a is divided by 8. | |||
Direct proportion summary
- y is directly proportional to x if there is a positive constant k such that y = kx.
- The symbol used for ‘is proportional to’ is
 . We write y
. We write y  x.
x. - If y is directly proportional to x, then the graph of y against x is a straight line through
the origin. The gradient of the line is the constant of proportionality.
Definition
The variable y is said to be inversely proportional to x if
![]() y =
y = 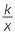
for a constant k. The number k is called the constant of proportionality.
The statement that, ‘y is inversely proportional to x’ is written symbolically as y 
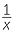 .
.
Notice that this could also be read as ‘y is directly proportional to 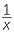 ’.
’.
The useful properties of inverse proportion are different from those of direct proportion. We list three important properties here.
- If y

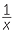 , then x
, then x 
 .
. - y

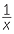 is equivalent to xy = k for a positive constant k. That is, the product is a constant. This is often a useful way to check when given data in table form.
is equivalent to xy = k for a positive constant k. That is, the product is a constant. This is often a useful way to check when given data in table form. - If y

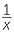 and x
and x 
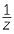 then y
then y  z.
z.
Velocity and time provide a good example of inverse proportion.
| We know that distance = speed × time | or | d = vt | ||
Rearranging gives time =  |
or | t = 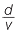 |
Now let the distance between two towns be 72km. The time t hours taken to cover this distance at v km/h is given by the formula
![]() t =
t = 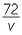
This is an example of inverse proportion. We write t 
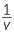 and say that t is inversely proportional to v, with constant of proportionality 72.
and say that t is inversely proportional to v, with constant of proportionality 72.
The graph of t against v is a part of a rectangular hyperbola but the graph of t against 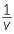
is a straight line with gradient 72.
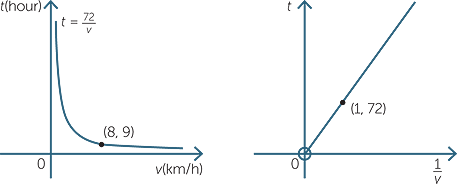
EXAMPLE
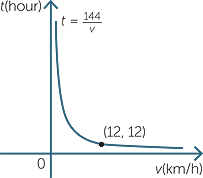
Suppose that two towns A and B are 144 km apart.
a Write down the formula for the time t hours taken when the journey from A to B is undertaken at a speed of v km/h.
b Draw a graph of t against v.
c If the car is driven at 24km/h, how long does it take to complete the journey?
d If the trip takes 90 minutes, what is the constant speed a car would need
to travel at?
Solution
| a | t = 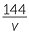
|
b |
|
| c |
|
When v = 24, t |
= |
|
|
= 6 hours |
||||
| d |
|
When t = |
|
|
|
So v |
= 144 × |
|||
|
= 96 km/h |
||||
There are many examples of inverse proportion in the topics covered at school. For example,
- A length 100 m of ribbon is to be divided amongst n people. The length that each person receives is inversely proportional to the number of people.
- For cylinders with volume 2 m3, the height of the cylinder is inversely proportional to the area of the base.
- The force between two charged objects is inversely proportional to the square of the distance between their centres.
- The illumination from a source of light is inversely proportional to the square of the distance from the source.
EXERCISE 4
The volume V cm3 of a gas kept at a constant temperature is inversely proportional to the pressure P kPa. If the volume is 500 cm3 when the pressure is 80 kPa, find the volume when the pressure is 25 kPa. (This an example of Boyle’s law)
EXERCISE 5
If a is inversely proportional to the cube of b and a = 2 when b = 3, find
|
a |
a when b = 2 |
b |
b when a = |
As with direct proportion, we can work out the effect on one variable of changing the other one.
EXAMPLE
Given that a 
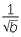 , what is the change in a when b is
, what is the change in a when b is
|
a |
doubled |
b |
halved? |
Solution
Since a 
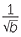 , we know that a
, we know that a![]() = k for some positive constant k.
= k for some positive constant k.
| a | When b = 1, | a | = k | ||
| When b = 2, | a |
= k | |||
| a | = 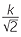 |
||||
| ≈ 0.707k |
So a is approximately 70.7% of its previous value.
Hence doubling b decreases a by approximately 29.3%.
| b | When b = 1, | a | = k | ||
| When b = 12, | a × 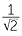 |
= k | |||
| a | = |
||||
| ≈ 1.414k |
That is, a is 141.4% of its previous value, hence halving b increases a
by approximately 41.4%.
EXERCISE 6
Given that y 
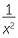 , what is the percentage change in
, what is the percentage change in
a![]() y when x is decreased by 10%
y when x is decreased by 10% ![]() b
b![]() x when y is increased by 10%?
x when y is increased by 10%?
Inverse proportion summary
- If y is inversely proportional to x then y is directly proportional to
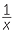 .
. - We write y

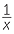 when y =
when y = 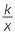 or xy = k, where k is a positive constant.
or xy = k, where k is a positive constant. - If y is inversely proportional to x then the graph of y against
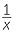 is a straight line and
is a straight line and
the gradient of the line is equal to the constant of proportionality. - If y

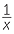 then for any two values x1 and x2 and the corresponding values y1 and y2:
then for any two values x1 and x2 and the corresponding values y1 and y2:
x1 y1 = x2y2 = k.
Proportionality in several variables
Often a particular physical quantity is dependent on several other variables. For instance, the distance d a motorist travels depends on both the speed v at which he travels and for the time t he travels, d = vt.
More generally, If y = kxz for a positive constant k we say that y is directly proportional to x and z. Similarly, if a = 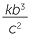 for a positive constant k we say that a is directly proportional to b3 and inversely proportional to c2.
for a positive constant k we say that a is directly proportional to b3 and inversely proportional to c2.
EXAMPLE
Assume a is directly proportional to b and to the square of c. If a = 36 when b = 3 and
c = 2, find a when b = 4 and c = 1
Solution
| a |  bc2 bc2 |
||
| so | a | = kbc2 for some constant k |
Substituting known values to find k.
| 36 | = k × 3 × 22 | ||
| k | = 3. | ||
| Hence | a | = 3bc2 |
When b = 4 and c = 1, a = 3 × 4 × 12 = 12
EXERCISE 7
The electrical resistance R ohms in a wire is directly proportional to its length L m and inversely proportional to the square of its diameter d mm. A certain wire 100 m long with
a diameter 0.4 mm has a resistance 1.4 ohms.
a Find the equation connecting R, L and D.
b Find the resistance (to one decimal place) of a wire of the same material if it is 150 m in length and has a diameter of 0.25 mm.
c If the length and diameter are doubled, what is the effect on the resistance?
d If the length is increased by 10% and the diameter is decreased by 5%, what is the percentage change on the resistance? (Give your answer correct to one decimal place.)
Two very important cases of direct proportion to several variables are the two inverse square rules.
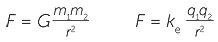
The first one is the fundamental law for gravitational force, and the second Coulomb’s law for electrostatic force between two electric charges. For the fundamental law of gravitation, R is the distance between the masses m1 and m2 and for Coulomb’s law it is the distance between the charges q1 and q2.
Other applications of proportion
Important examples arise in mathematics where there is direct proportion to a function. One important case is where y  2ax which provides a model for both exponential growth and exponential decay.
2ax which provides a model for both exponential growth and exponential decay.
An interesting case of proportion is Snell's Law. When light is refracted through a transparent substance, the angle θ of incidence is related to the angle Φ of refraction
by the equation
![]() sin θ = k sin Φ, for some constant k, called the refractive index.
sin θ = k sin Φ, for some constant k, called the refractive index.
Thus one has to take the sine of both the angles to obtain a statement of proportionality.
Functions and calculus
This topic is the beginning of the students understanding of the applications of functions and should begin to indicate the extent of applications of mathematics in many diverse areas. It leads on to all aspect of the study of functions and of calculus. A graphical introduction to rates is provided by the ideas of proportion.
The history of proportion starts with the ancient Greeks. It was developed in Book V of Euclid and used for geometry in Book VI. Many of the questions raised in Euclid were not satisfactorily resolved until the work of Weierstrass, Cantor and Dedekind in the 19th century. Some of this is discussed in the module, Rates and Ratios.
Proportion is such a fundamental idea it appeared in more mundane manifestations.
One such case is the following:
Rule of three
The rule of three was a shorthand version for a particular form of cross multiplication, often taught to students by rote. Here is an example of the type of problem.
If three bananas cost 60 cents how much will 7 bananas cost? Using the rule of three you would multiple 60 by 7 and divide by 3.
The method is equivalent to solving the equation, 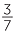 =
= 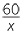 . Without modern algebraic notation the language to explain why the rule of three works was difficult to explain.
. Without modern algebraic notation the language to explain why the rule of three works was difficult to explain.
The Rule of Three originated from the Hindu mathematicians Brahmagupta (circa 628 AD) and Bhaskara (circa 1150 AD). It appeared in Europe from the 15th century and was extremely popular with merchants. An English arithmetician of the 17th century wrote, ‘The rule of three is commonly called the golden rule ; and indeed it might be so termed; for as gold transcends all other metals so doth this rule all others in arithmetic.’
Of course, we can rewrite the solution to this question in terms of the proportion statement, ‘Cost of n bananas in cents = 20n’.
The ideas of ratios were also used in Greek science. For example Archimedes
(287 − 212 BC) achieved results about the balancing of a uniform bar. We illustrate
this through an example.
A weight of 3 kilograms is placed 120 cm from the fulcrum on which a bar is balanced. Balance can be achieved if a weight of m kilograms is placed x cm away from the fulcrum on the other side of the fulcrum so that mx = 120 × 3. Hence the distance at which the weight is placed from the fulcrum necessary for balance is inversely proportional to the weight. The modern term for this product is the moment.
Archimedes treatise On floating bodies also contains material which uses proportions. Archimedes’ principle mentioned earlier in this module is an example of his results in
this area.
Proportion, science and mathematics
We will briefly discuss the development of some aspects of mathematics and science up to the early 18th century. We cannot attempt to give any complete picture of this but comment that science and mathematics developed very closely together up until modern times and proportion was a central concept in this development.
The roots of a lot of mathematics lie in the physical sciences.
Some progress had been made in medieval times. The Merton Scholars at Oxford in the mid fourteenth century studied motion with constant acceleration and the following was attributed to them.
A body moving with uniformly accelerated motion in a given time exactly the same distance it would move at constant velocity equal to its instantaneous velocity at the midpoint of the time period under consideration.
Nicole of Oresme (1323 − 1382) developed a diagrammatic representation of motion. He arrived at a representation of the distance travelled as an area whose two dimensions (which are represented by perpendicular lines) were was time and the other velocity. He thus introduced an idea very similar to rectangular coordinates. His conclusions were to be reiterated and further developed by Galileo. This work was done well before a clear notion of coordinate geometry had been developed.
Proportion was part of the language of the mathematics and physics from the time of Galileo (1564 − 1642). Many manuscripts originating from the Greeks came from the Byzantine Empire and the Arabs, and many thought that these manuscripts were the catalyst for the rebirth of scientific thought In Europe. Galileo achieved the result that for a body moving with constant acceleration the distance travelled is proportional to the square of the time of travel.
Kepler (1571 − 1630) also was familiar with the work of the ancient Greeks. He followed Copernicus and developed his theories further. His laws of planetary motion use the language of proportion.
Kepler's laws are:
- The orbit of every planet is an ellipse with the Sun at one of the two foci.
- A line joining a planet and the Sun sweeps out equal areas during equal intervals of time. In terms of proportion this can be written as, ‘The area swept out in a given time interval by the line joining the sun to the planet is proportional to the length of the time interval’.
- The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
Huygens (1629 − 95) obtained further results and found that for a body moving in a circular path at constant speed v has acceleration directed towards the centre of the circle of 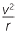 . The force acting on the particle is proportional to the square of the velocity and inversely proportional to the radius of the circle.
. The force acting on the particle is proportional to the square of the velocity and inversely proportional to the radius of the circle.
Sir Isaac Newton’s (1642 − 1727) work followed on from the earlier scientists discussed above. He was born in the year that Galileo died. He explained mathematically the results obtained by Galileo and Kepler. He used calculus, which he had developed, to achieve these results. He obtained the fundamental law for gravitational forces, F = G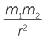 , which can be read as, ‘Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is directly proportional to the product of the two masses and inversely proportional to the square of the distance between the point masses.’
, which can be read as, ‘Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is directly proportional to the product of the two masses and inversely proportional to the square of the distance between the point masses.’
Newton’s second law of motion is also framed in terms of proportion.
‘A change in motion is proportional to the motive force impressed and takes place in the straight line in which that force is impressed’ (F = ma).
Proportion continued to be a key idea through the 18th and 19th centuries and its importance, of course, continues to this day.
EXERCISE 1
67.2 milligrams
EXERCISE 2
1.618 (a decimal approximation of the golden ratio)
EXERCISE 3
1852 kW
EXERCISE 4
1600cm3
EXERCISE 5
| a | 6.75 | b | 4 |
EXERCISE 6
| a | y is increased by approximately 23.5% | b | x has decreased by approximately 4.7% |
EXERCISE 7
| a | R = 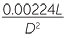 |
b | 5.4 ohm | |||
| c | resistance is halved | d | resisistance is increased by 21.9% |
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()