The Improving Mathematics Education in Schools (TIMES) Project
- Facility with solving linear equations
- All of the content of the module, Factorisation.
- Facility with arithmetic of positive and negative numbers
In the module, Linear Equations we saw how to solve various types of linear equations. Such equations arise very naturally when solving elementary everyday problems.
A linear equation involves the unknown quantity occurring to the first power, thus,
for example,
![]() 2x − 7 = 9
2x − 7 = 9
![]() 3(x + 2) − 5(x − 8) = 16
3(x + 2) − 5(x − 8) = 16
![]()
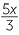 = 8
= 8
are all examples of linear equations.
Roughly speaking, quadratic equations involve the square of the unknown. Thus, for example, 2x2 − 3 = 9, x2 − 5x + 6 = 0, and 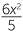 − 4x = 2x − 1 are all examples of quadratic equations. The equation
− 4x = 2x − 1 are all examples of quadratic equations. The equation 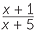 =
= 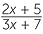 is also a quadratic equation.
is also a quadratic equation.
The essential idea for solving a linear equation is to isolate the unknown. We keep rearranging the equation so that all the terms involving the unknown are on one side of the equation and all the other terms to the other side. The rearrangements we used for linear equations are helpful but they are not sufficient to solve a quadratic equation. In this module we will develop a number of methods of dealing with these important types of equations.
While quadratic equations do not arise so obviously in everyday life, they are equally important and will frequently turn up in many areas of mathematics when more sophisticated problems are encountered. Both in senior mathematics and in tertiary and engineering mathematics, students will need to be able to solve quadratic equations with confidence and speed. Surprisingly, when mathematics is employed to solve complicated and important real world problems, quadratic equations very often make an appearance as part of the overall solution.
The history of quadratics will be further explored in the History section, but we note here that these types of equations were solved by both the Babylonians and Egyptians at a very early stage of world history. The techniques of solution were further refined by the Greeks, the Arabs and Indians, and finally a complete and coherent treatment was completed once the notion of complex numbers was understood. Thus quadratic equations have been central to the history and applications of mathematics for a very long time.
A quadratic is an expression of the form ax2 + bx + c, where a, b and c are given numbers and a ≠ 0.
The standard form of a quadratic equation is an equation of the form
![]() ax2 + bx + c = 0, where a, b and c are given numbers and a ≠ 0.
ax2 + bx + c = 0, where a, b and c are given numbers and a ≠ 0.
We seek to find the value(s) of which make the statement true, or to show that there are no such values.
Thus, for example, the values x = 3 and x = 2 satisfy the equation, x2 − 5x + 6 = 0. This is easily checked by substitution.
These values are called the solutions of the equation. Linear equations that are written in the standard form , ax + b = 0, a ≠ 0, have one solution. Quadratic equations may have no solutions, one solution, or, as in the above example, two solutions.
There are two special types of quadratic equations, that are best dealt with separately.
Quadratic equations with no term in x
When there is no term in x we can move the constant to the other side.
EXAMPLE
Solve x2 − 9 = 0.
Solution
| x2 − 9 | = 0 | |
| x2 | = 9 | |
| x | = 3 or x = −3. |
(Note that this equation can also be solved by factoring using the difference of squares identity. While this is a valid approach, it makes a simple problem appear complicated, which is, in general, not a good way to do mathematics.)
Quadratic equations with no constant term
EXAMPLE
Solve x2 − 9x = 0.
Solution
In this case, we can write
![]() x2 − 9 = 0
x2 − 9 = 0
![]() x(x − 9) = 0
x(x − 9) = 0
Since the product of the two factors is 0, one or both of the factors is zero, x(x) − 9 = 0.
so![]() x = 0 or x − 9 = 0
x = 0 or x − 9 = 0
Hence the two solutions are or x = 0, or x = 9.
These two methods work just as well when the coefficient of x2 is not one.
The two previous examples were relatively easy since in the first case it was easy to isolate the unknown while in the second, a common factor enabled the left-hand side to be easily factored.
Solving quadratic equations with three terms
We will now deal with the equation ax2 + bx + c = 0 in which neither a nor b nor c are zero.
There are three basic methods of solving such quadratic equations:
- by factoring
- by completing the square
- by the quadratic formula
Each method is important and needs to be mastered. Different situations will require different approaches, and while the last two methods always work, the method of factoring is very quick and accurate, provided the equation has rational solutions.
Solving quadratic equations by factoring
The method of solving quadratic equations by factoring rests on the simple fact, used in example (2) above, that if we obtain zero as the product of two numbers then at least one of the numbers must be zero.
That is, if AB = 0 then A = 0 or B = 0
In the module, Factorisation, we first saw how to factor monic quadratics, then we learnt how to factorise non-monic quadratics.
To factor x2 + bx + c we try to find two numbers whose sum is b and whose product is c. We now apply this idea to solving quadratic equations.
EXAMPLE
Solve x2 − 7x + 12 = 0.
Solution
We factor the left-hand side by finding two numbers whose product is 12 and whose sum is −7. Clearly, −4, −3 are the desired numbers. We can then factor as:
![]() x2 − 7x + 12 = 0
x2 − 7x + 12 = 0
![]() (x − 4)(x − 3) = 0
(x − 4)(x − 3) = 0
Since the product of the two factors is zero, one of the factors is zero.
| Thus | x − 4= 0, or x − 3 = 0 | |
| so | x = 4, or x = 3 |
The same method can also be applied to non-monic quadratic equations. A non-monic quadratic equation is an equation of the form ax2 + bx + c = 0, where and are given numbers, and a ≠ 1 or 0. This is the general case.
Thus 2x2 + 5x + 3 = 0 is an example of a non-monic quadratic equation.
EXAMPLE
Solve the equation 2x2 + 5x + 3 = 0.
Solution
Using the factoring method from the module Factorisation , we multiply 2 and 3 to give 6 and find two numbers that multiply to give 6 and add to give 5. The desired numbers are 2 and 3. We use these numbers to split the middle term and factor in pairs.
![]() 2x2 + 5x + 3 = 0
2x2 + 5x + 3 = 0
![]() 2x2 + 2x + 3x + 3 = 0
2x2 + 2x + 3x + 3 = 0 ![]() (split the middle term)
(split the middle term)
![]() 2x(x + 1) + 3(x + 1) = 0
2x(x + 1) + 3(x + 1) = 0
![]() (x + 1)(2x + 3) = 0
(x + 1)(2x + 3) = 0
We can now equate each factor to zero and obtain
![]() x + 1 = 0, or 2x + 3 = 0
x + 1 = 0, or 2x + 3 = 0
![]() x = −1, or x = −
x = −1, or x = − .
.
As was pointed out in the module, Factorisation, the order in which the middle terms are written does not affect the final factorisation, and hence does not effect the solutions of the quadratic.
EXERCISE 1
Solve the equations.
a![]() 4x2 − 20 = 0
4x2 − 20 = 0 ![]() b
b![]() x2 − x − 12 = 0
x2 − x − 12 = 0![]() c
c![]() 3x2 + 2x − 8 = 0
3x2 + 2x − 8 = 0
Note: While the values of which satisfy 2x2 + 5x + 3 = 0 are x = −1 or x = − , we often say that the solution of 2x2 + 5x + 3 = 0 are x = −1 and x = −
, we often say that the solution of 2x2 + 5x + 3 = 0 are x = −1 and x = − .
.
Common simplifications of quadratics
It is often convenient to simplify a quadratic equation before any method of solution is applied.
- If the coefficient of x2 is negative multiply through by −1.
−x2 + 5x −6 = 0 becomes x2 − 5x + 6 = 0 - ‘multiply out fractions’
 −
− 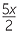 + 3 becomes x2 − 5x + 6 = 0
+ 3 becomes x2 − 5x + 6 = 0 - If there is a common factor divide through by it.
3x2 − 15x + 18 = 0 becomes x2 − 5x + 6 = 0
Equations that can be rearranged to be a quadratic equation in standard form
The standard form for a quadratic equation is ax2 + bx + c = 0, a ≠ 0.
We may however, be given a quadratic equation that is not in this form and so our first step is to re-write the equation into this standard form.
EXAMPLE
Solve 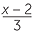 =
=  .
.
Solution
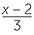 |
=  |
|||
| x(x − 2) | = 3 × 5 | (cross-multiplication) | ||
| x2 − 2x | = 15 | |||
| x2 − 2x − 15 | = 0 | (Rearrange) | ||
| (x + 3)(x − 5) | = 0 | |||
| x + 3 | = 0 or x − 5 = 0 | |||
| x | = −3 or x = 5 | |||
EXERCISE 2
Solve  −
− 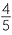 =
= 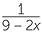 .
.
Applications
EXAMPLE
A rectangle has one side 3cm longer than the other. The rectangle has area 28cm2.
What is the length of the shorter side?
Solution
Let x cm be the length of the shorter side. The other side has length (x + 3)cm.
Area = x(x + 3) = 28cm2
![]() x2 + 3x − 28 = 0
x2 + 3x − 28 = 0
![]() (x − 4)(x + 7) = 0
(x − 4)(x + 7) = 0
![]() x − 4 = 0 or x + 7 = 0
x − 4 = 0 or x + 7 = 0
![]() x = 4 or x = −7
x = 4 or x = −7
Since length must be positive, the solution to the problem is x = 4. The shorter side has length 4cm.
EXERCISE 3
Each number in the sequence 5, 9, 13, 17, … is obtained by adding 4 to the previous number. The sum S of the first n numbers in the sequence is given by S = 2n2 + 3n.
How many numbers must be added to make the sum equal to 152?
Completing the square
The quadratic equations encountered so far, had one or two solutions that were rational. There are many quadratics that have irrational solutions, or in some cases no real solutions at all.
For example, it is not easy at all to see how to factor the quadratic x2 − 5x − 3 = 0.
Indeed it has no rational solutions. We will see shortly that the solutions are x = 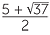
and x = 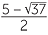 .
.
To deal with more general quadratics, we employ a technique known as completing the square. Historically, this was the most commonly used method of solution.
The technique of completing the square is used not only for solving quadratic equations, but also in further mathematics for such things as:
- finding the centre and radius of a circle − given its algebraic equation,
- finding the maximum or minimum of a quadratic function,
- finding the axis of symmetry of a parabola,
- putting integrals into standard form in calculus.
This is an important technique that will appear in other settings and so is a basic skill that students who intend to proceed to senior mathematics need to master.
In the early stages, students will need to be told when to apply which method.With experience, they will use completing the square whenever they cannot see how to apply the factor method shown above. The method of completing the square works in every case, including the situation in which the factor method applies.
In earlier modules we have seen the two identities referred to as perfect squares:
![]() a2 + 2ab + b2 = (a + b)2 and a2 − 2ab + b2 = (a − b)2.
a2 + 2ab + b2 = (a + b)2 and a2 − 2ab + b2 = (a − b)2.
Thus, for example, x2 + 6x + 9 = (x + 3)2 and x2 − 4x + 4 = (x − 2)2.
Notice that in the quadratics above, the constant term in each case is the square of half the coefficient of x. The method of completing the square simply involves adding in a number make a given quadratic expression into a perfect square.
Completing the square in an expression
We begin by completing the square on the quadratic expression x2 + 2x − 6.
We focus on x2 + 2x and ask: What number must be added to x2 + 2x to make the expression into a perfect square?
The key step is to take half the coefficient of and square it. The same rule applies when the coefficient of is x negative.
In this case, the answer is 1, since x2 + 2x + 1 = (x + 1)2.
This can be seen diagrammatically, where a square is added to 'complete the square’.
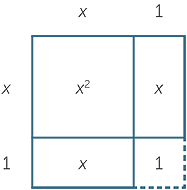
We can then write:
| x2 + 2x − 6 | = (x2 + 2x + 1) − 1 − 6 | (add and subtract 1) | ||
| = (x + 1)2 − 7. |
In the case when the coefficient of x is odd, we will need to use fractions. For example,
to complete the square on x2 − 3x + 1, we note that half of −3 is − and
and  . Hence we have x2 − 3x + 1 = x2 − 3x +
. Hence we have x2 − 3x + 1 = x2 − 3x +  −
−  + 1 = x −
+ 1 = x −  2 −
2 −  .
.
Solving quadratic equations by completing the square
We can now apply the method of completing the square to solve quadratic equations. To complete the square for an equation, we will add in a factor on each side to produce a square.
EXAMPLE
Solve x2 + 2x − 6 = 0.
Solution
It is easiest to move the constant term onto the other side first and then complete the square.
| x2 + 2x − 6 | = 0 | |||
| x2 + 2x | = 6 | |||
| x2 + 2x + 1 | = 7 | (Add 1 to both sides to produce a square) | ||
| (x + 1)2 | = 7 |
We can now take the positive and negative square roots to obtain
| x + 1 = |
||
| so, | x = −1 + |
Notice that the solutions are irrational, and so this equation could not be easily solved using the factoring method.
EXAMPLE
Solve x2 − 6x − 2 = 0.
Solution
| x2 − 6x − 2 | = 0 | ||
| x2 − 6x + 9 − 9 − 2 | = 0 |
||
| (x − 3)2 | = 11 | ||
| x − 3 | = 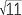 or x − 3 = − or x − 3 = −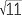 |
||
| Hence | x | = 3 + 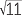 or x = 3 − or x = 3 − 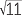 . . |
|
There are, of course, quadratic equations which cannot be solved using real numbers.
For example, if we apply the method to the equation x2 − 6x + 12 = 0, we obtain
(x − 3)2 = −3 and (x − 3)2 ≥ −3 since the equation cannot be solved.
EXERCISE 4
Solve x2 − 5x − 3 = 0 by completing the square and also show that x2 − 5x + 7 = 0 has
no solutions.
Non-monic quadratics
You will have noticed that we have not solved any non-monic quadratics by completing the square. This is generally rather tricky for students to complete and non-monic quadratics that cannot be solved by factoring can always be solved using the quadratic formula.
To solve a non-monic quadratic by completing the square, it is easiest to divide the equation by the leading coefficient and so make the quadratic monic. This will lead to fractions as the following example shows.
EXAMPLE
Solve 3x2 − 5x + 1 = 0.
Solution
Divide the equation by 3 and shift the constant term to the other side.
| 3x2 − 5x + 1 | = 0 | |
x2 −  x x |
= −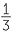 |
|
x2 −  x + x +  |
=  − − 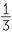 |
|
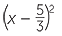 |
= 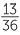 |
|
| So, | x | = 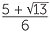 or x = or x = 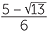 . . |
As mentioned above, these solutions can also be found using the quadratic formula.
The quadratic formula
The method of completing the square always works. By applying it to the general quadratic equation ax2 + bx + c = 0 we obtain the well-known quadratic formula.
To derive the formula, we will begin by multiplying the equation through by 4a, which although not the usual first step in completing the square, will make the algebra much easier.
![]() ax2 + bx + c = 0
ax2 + bx + c = 0
![]() 4a2x2 + 4abx + 4ac = 0
4a2x2 + 4abx + 4ac = 0
We now note that (2ax + b)2 = 4a2x2 + 4abx + b2 so adding b2 will produce a square.
![]() 4a2x2 + 4abx = −4ac
4a2x2 + 4abx = −4ac
![]() 4a2x2 + 4abx + b2 = b2 − 4ac
4a2x2 + 4abx + b2 = b2 − 4ac
![]() (2ax + b)2 = b2 − 4ac.
(2ax + b)2 = b2 − 4ac.
We pause at this stage to note that if b2 − 4ac is negative, then there is no solution.
If b2 − 4ac is positive, we then proceed to take the positive and negative square roots to solve for x. If b2 − 4ac is equal to 0, then there will only be 1 solution. We suppose then that b2 − 4ac is positive and proceed to find the solutions.
![]() (2ax + b)2 = b2 − 4ac
(2ax + b)2 = b2 − 4ac
![]() 2ax + b =
2ax + b =  or 2ax + b = −
or 2ax + b = −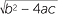
![]() x =
x = 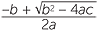 or x = −
or x = −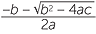 .
.
This last formula is called the quadratic formula, sometimes written as x = 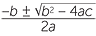 .
.
If the quantity b2 − 4ac = 0 then there will only be one solution, x = −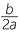 .
.
In this case, the quadratic will be a perfect square. The quantity b2 − 4ac plays an important role in the theory of quadratic equations and is called the discriminant.
Thus, in summary, when solving ax2 + bx + c = 0, first calculate the discriminant b2 − 4ac. Then,
- if b2 − 4ac is negative, then there is no solution.
- if b2 − 4ac is positive, then the solutions are x =
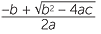 , x = −
, x = −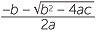 .
. - if b2 − 4ac is zero, then there is only one solution x = −
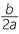 .
.
While students do not need to learn the derivation of the formula, they do need to remember the formula itself.
Note: If b2 − 4ac is zero, then the quadratic is a perfect square.
EXAMPLE
Solve x2 − 10x − 3 = 0 by
a using the formula. b completing the square.
Solution
| a | Here a = 1, b | = −10, c = −3, | |
| so b2 − 4ac | = 100 + 12 | ||
| = 112. |
x = 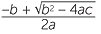 |
|
or | |
x = 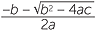 |
||
x = 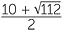 |
or | x = 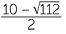 |
||||
x = 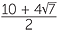 |
or | x = 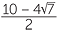 |
(Simplify the surd.) | |||
x = 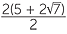 |
or | x = 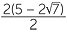 |
||||
x = 5 + 2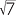 |
or | x = 5 − 2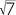 |
| b | x2 − 10x − 3 | = 0 | |||||
| x2 − 10x + 25 − 25 − 3 | = 0 | ||||||
| (x − 5)2 | = 28 | ||||||
| x − 5 | = 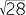 |
|
or | |
x − 5 = −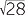 |
||
| x | = 5 + 2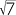 |
or | x = 5 − 2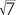 |
EXERCISE 5
Re-solve the quadratic equation 3x2 − 5x + 1 = 0 using the quadratic formula.
A further application
One very interesting application involves a number known to the Greeks as the golden ratio.
A golden rectangle is a rectangle such as ACDF drawn below, with sides of length 1 and x, and with the property that if a 1 × 1 square (BCDE)is removed, the resulting rectangle (ABEF) is similar to the original one. That is, ACDF is an enlargement of ABEF.
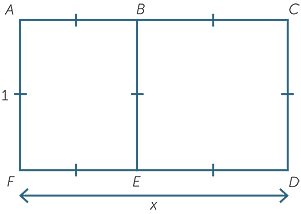
The Greeks regarded the relative dimensions of the rectangle ABEF as ‘most pleasing
to the eye’. The front facade of the Parthenon has its sides in this ratio.
Since the rectangles are similar, their sides are in proportion. Now EF = x − ED = x − 1,
and  =
= 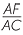 . Thus,
. Thus, 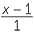 =
=  .
.
We can multiply both sides by and re-arrange to form a quadratic equation.
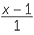 =
= 
x2 − x = 1
x2 − x − 1 =0.
Applying the quadratic formula, with a = 1, b = −1, c = −1 and b2 − 4ac = 5, we have
![]() x =
x = 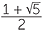
![]() or
or ![]() x =
x = 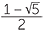 .
.
The second of these numbers is negative and so cannot be the solution of the given problem. Hence the value of x is 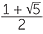 which is approximately, correct to three decimal places. This number is called the golden ratio and arises in several places in mathematics, some of the them quite unexpected.
which is approximately, correct to three decimal places. This number is called the golden ratio and arises in several places in mathematics, some of the them quite unexpected.
Equations reducible to quadratics
We conclude out discussion by mentioning equations that are not strictly quadratic, but can be reduced to a quadratic equation by a simple substitution.
EXAMPLE
Solve 22x − 5 × 2x − 24 = 0.
Solution
Put u = 2x then the equation becomes u2 − 5u − 24 = 0.
This equation factors as (u − 8)(u + 3) = 0
and so or u = 8 or u = −3.
Replacing u, we have 2x = 8, 2x = −3.
The second equation has no solution, since 2x > 0, while the first equation has solution x = 3.
EXERCISE 6
Solve the equation (x2 − 2x)2 − 11(x2 − 2x) + 24 = 0.
In the module, The quadratic function, we will look in detail at the graphs of the quadratic function y = ax2 + bx + c, which represents a parabola. The technique of completing the square that we have gone through in this chapter will be used to find the axis of symmetry of the parabola.
Quadratic inequalities
Replacing the sign = with an inequality sign produces a quadratic inequality. These have many applications including finding the domain and range of a given function.
The method of solution is similar to that for solving quadratic equations.
EXAMPLE
Solve x2 − x − 2 < 0.
Solution
Factoring the equation, we have (x − 2)(x + 1) < 0
Now if the product of two numbers is negative, then the numbers must have opposite sign. Since (x − 2) is smaller than (x + 1), we have (x − 2) < 0 and (x + 1) > 0 giving x < 2
and x > −1.
We can combine these to write, −1 < x < 2.
Cubic equations
Cubic equations are generally not covered in detail in the school syllabus, but arise as a natural generalization of quadratic equations.
For example, x3 − x + 2 = 0 is an example of a cubic equation.
In the module, Polynomials, a factoring method will be developed to solve cubic equations that have rational roots.
Just as there is quadratic formula for solving quadratic equations, there is also a cubic formula for solving cubic equations. There is a simple procedure for taking a general cubic equation and removing the term involving Thus, we may assume that our cubic is in the form x3 − px + q = 0. (This is sometimes called a depressed cubic, or a cubic in Weierstrass form).
In this case, a clever procedure, going back to the 15th century, enables us to solve the cubic and write the solution as
![]() x =
x = 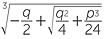 +
+ 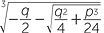 .
.
The quantity 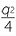 +
+ 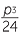 under the square root sign above is called the discriminant of the cubic. Cubic equations may have either 1, 2 or 3 real roots. The above formula only produces 1 real root.
under the square root sign above is called the discriminant of the cubic. Cubic equations may have either 1, 2 or 3 real roots. The above formula only produces 1 real root.
EXERCISE 7
Apply the formula to find a real root of x3 − x − 1 = 0. (Using calculus, it can be shown that this equation has only 1 real root.)
Perhaps surprisingly, quadratic equations are known from quite early on in the history of mathematics. The Babylonians were solving quadratic equations as early as 2000 BC. Their method of solution was different from ours and was expressed verbally as a series of steps (with no proof.) They also solved non-linear simultaneous equations that lead in standard algebra to quadratics. For example, x + y = 10, xy = 5.
The Babylonian method of solution
It should be emphasised that the following method, although interesting, is not recommended for the classroom.
We illustrate using the equation x2 − 2x − 8 = 0.
| Step 1 | Take the constant term on the other side and factor the left-hand side. | |
| x(x − 2) = 8. | ||
| Step 2 | Put a equal to the average of these terms, that is a = x − 1. Then x = a + 1, (x − 2) = a − 1. |
|
| Step 3 | Substitute and solve for using the difference of squares identity. | |
| x(x − 2) = 8 | ||
| (a + 1)(a − 1) = 8 | ||
| a2 − 1 = 8 | ||
| a2 = 9. |
Now the Babylonians did not use negative numbers, so for them the only solution is a = 3, and so x = 4.
This method can also be used to find irrational solutions.
EXERCISE 8
Use the Babylonian method to solve x2 + 2x − 6 = 0.
The first known occurrence of a quadratic equation in Egyptian mathematics occurs in the Berlin Papyrus, dating from the Middle Kingdom in Egypt (c.2160−1700). The problem is:
To divide 100 square measures into two squares such that the side of one of the squares shall be three fourths the side of the other.
Translated into modern notation, this problem requires us to solve the simultaneous equations
![]() x2 + y2 = 100, and y =
x2 + y2 = 100, and y =  x.
x.
The Egyptians gave the solution as a sequence of unexplained steps which basically use ideas of proportion.
The Greeks also solved quadratic equations, but used graphical/geometric methods to do so.
Euclid (Book 2, Proposition 11) solved the quadratic x2 + ax = a2 geometrically. The method used was basically a form of completing the square.
In later books in the Elements (e.g. Proposition 11 in Book IV), Euclid gives geometric constructions equivalent to solving a general quadratic equation. There is no algebraic solution in Euclid.
Throughout antiquity various rules were given for special cases and types of quadratics.
The so-called Hindu Rule was first given by Sridhara in about 1025. It said:
Multiply both sides of the equation by a number equal to four times the [co-efficient] of the square, and add to them a number equal to the square of the original [co-efficient] of the unknown quantity. [Then extract the root].
That is, given ax2 + bx = c multiply by 4a and add to b2 obtain 4a2x2 + 4abx + b2 = b2 + 4ac, whence 2ax + b = + , and so the equation can be solved. Notice that is essentially our derivation of the quadratic formula.
, and so the equation can be solved. Notice that is essentially our derivation of the quadratic formula.
Al-Khwarizmi (9th century A.D.), in the first Arabic text-book on algebra, solves quadratics of the form x2 + ax = b by completing the square.
He adds  a2 to both sides and obtains x +
a2 to both sides and obtains x +  a =
a = 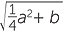 , from which he can extract x.
, from which he can extract x.
Many other general methods also have appeared.
Interestingly the first written appearance of the method using factorisation did not occur until 1631, and an explicit form of the quadratic formula does not appear until Vieta c.1580.
Although particular examples of cubic equations arose in antiquity, the general cubic equation was not solved until the 15th century, as was the quartic equation. Attempts to find formula for the solution of the quintic (equations of degree 5) and higher degree equations, in the same spirit as the quadratic formula, were shown in the 19th century to be impossible. That means that there is no general formula for the solution of equations of degree 5 or higher in terms of radicals, that is, using combinations of square, cube, fourth or higher roots alone.
EXERCISE 1
a x = ![]() or x = –
or x = –![]() b x = 4 or x = –3 c x = –2 or x =
b x = 4 or x = –3 c x = –2 or x = 
EXERCISE 2
x = 2 or x = 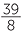
EXERCISE 3
n = 8
EXERCISE 4
x = 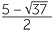 or x =
or x = 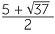
x2 – 5x + 7 = 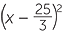 +
+ 
EXERCISE 5
x =  or x =
or x = 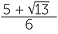
EXERCISE 6
x = –2 or x = –1 or x = 3 or x = 4
EXERCISE 8
x = –1 + ![]() or x = –1 –
or x = –1 –![]()
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

