The Improving Mathematics Education in Schools (TIMES) Project

return to index

Data Investigation and interpretation

Statistics and Probability : Module 3Year : 5

June 2011

PDF Version of module

return to top

Assumed background from F-4

It is assumed that in Years F-4, students have had many learning experiences involving choosing and identifying questions or issues from everyday life and familiar situations and planning statistical investigations that involve data in which observations fall into natural or assembled categories.

It is assumed that students have had learning experiences in recording, classifying and exploring such data, and have seen and used tables, picture graphs and column graphs of categorical data with natural or assembled categories.

It is assumed that some of these experiences involved count data with a small number of different counts that were treated as categories.

return to top

Motivation

Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.

A natural environment for learning statistical thinking is through experiencing the process of carrying out real statistical data investigations from first thoughts, through planning, collecting and exploring data, to reporting on its features. Statistical data investigations also provide ideal conditions for active learning, hands-on experience and problem-solving.

Real statistical data investigations involve a number of components: formulating a problem so that it can be tackled statistically; planning, collecting, organising and validating data; exploring and analysing data; and interpreting and presenting information from data in context. A number of expressions to summarise the statistical data investigative process have been developed but all provide a practical framework for demonstrating and learning statistical thinking. One description is Problem, Plan, Data, Analysis, Conclusion (PPDAC); another is Plan, Collect, Process, Discuss (PCPD).

No matter how it is described, the elements of the statistical data investigation process are accessible across all educational levels.

return to top

Content

In this module, in the context of statistical data investigations, we introduce measurement data. We contrast measurement data with categorical data and count data, and also consider more general examples of count data than in the Year 4 module.

Some examples of measurement data are:

All measurement data need units of measurement and observations are recorded in the desired units of measurement.

In categorical data each observation falls into one of a number of distinct categories. Such data are everywhere in everyday life. Some examples are:

Sometimes the categories are natural, such as with gender or direction on a road, and sometimes they require choice and careful description, such as type of dwelling.

Each observation in a set of count data is a count value. Count data occur in considering situations such as:

This module uses a number of examples to illustrate these different types of data and to develop the statistical data investigation process through the following:

Such phases lend themselves to representation on a diagram, as follows.

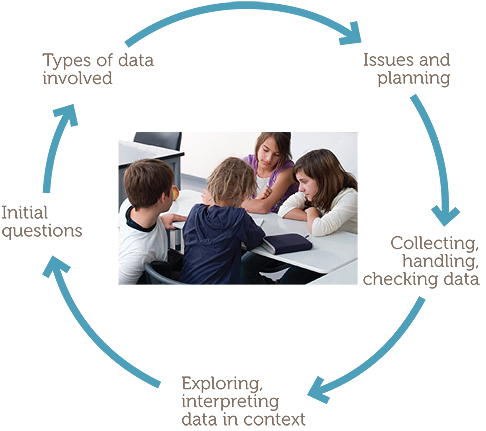
The examples consider situations familiar and accessible to Year 5 students, and build on the situations considered in F- 4.

return to top

Initial questions that can motivate an investigation.

The following are some examples of questions that involve collecting and investigating measurement, categorical or count data.

A
How long does it take you to get to school in the morning?

B
How tall are you? What is the length of your arm span from fingertip to fingertip when you stretch your arms out sideways? What is the difference between your span and your height? How does it compare with others in your class?

C
For how long can you balance a book on your head? How do you compare with others in your class? How much does it vary when you do it lots of times?

D
How many shots are there in a tennis game before each point is won? How much
do they vary over a whole match?

E
How much time is there between shots at goal in a football (soccer) match?
How much variation is there over a match?

F
How many passes are there in a football or netball match? How much does this number vary over matches?

G
How many vehicles go past your school every 2 minutes?

H
How many different types of trees are there in your school’s neighbourhood?
How would you classify them? How many trees are there of each type in the
playing fields of your school or in a local park?

I
How many times does the word 'Harry' appear per page in a Harry Potter book?
How much does this vary over pages?

J
How many different types of letterboxes are there in your neighbourhood?
How would you classify them? How many letterboxes of each type are there
in your neighbourhood?

The above are examples of just some of the many questions that can arise that involve measurement, count or categorical data. Some of these questions are used here to explore the progression of development of learning about data investigation and interpretation. The focus in this module in exploring and interpreting is on one dataset at a time; for example, in Example B, data on height and span would be explored separately to each other.

return to top

Measurement, categorical and count data

Before considering issues and planning, collecting, exploring and interpreting data with some of the above examples, the types of data are considered for all the examples. Also considered below are the general types of subjects − that is, on or from what will the observations be collected or observed.

A
The times for different students to get to school are measurement data. The observations are taken for each selected student.

B
The heights and spans of students are measurement data. There are two measurement variables, height and span, and from these can be calculated another, span-height. The observations are taken for each selected student.

C
How long different students can balance a book on their heads are measurement data. The observations are for each student. Repeatedly measuring how long one student can balance a book on his or her head gives a different type of set of measurement data in which the observations are taken for each attempt for that student.

D
Recording the number of shots before each point is won in a tennis match gives a set of count data. For each point we count the number of shots until the point is won. The observations are observed for each point.

E
Recording the times between shots at goal in a football (soccer) match gives a set of measurement data. The observations are observed for each shot at goal.

F
Recording the number of passes in a series of football or netball matches gives a set of count data. The observations are collected for each match.

G
Recording the numbers of cars passing in 2 minutes over a number of 2 minute intervals gives a set of count data. The observations are collected for each 2 minutes.

H
Type of tree is categorical. Classifying the trees in a region into types gives a set of categorical data. The observations are taken for each tree sampled.

I
Recording the number of times the word 'Harry' appears on a sample of pages from a Harry Potter book gives a set of count data. The observations are recorded for each selected page.

J
Type of letterbox is categorical. Classifying the letterboxes in your neighbourhood into types gives a set of categorical data. The observations are per type.

General statistical notes for teachers

Types of data − types of variables

When we collect or observe data, the ‘what’ we are going to observe is called a statistical variable. You can think of a statistical variable as a description of an entity that is being observed or is going to be observed. Hence when we consider types of data, we are also considering types of variables.

Measurement variables are examples of continuous variables; continuous variables can take any values in intervals. More about continuous variables is seen in Years 7 and upwards. Measurement data have units of measurement and are recorded with a certain precision that depends on the measuring instrument, the choice of the investigator and practical restrictions.

A categorical variable takes names or values that represent distinct categories. The categories are usually natural categories such as cat or dog, male or female, but often there are many possible categories or different possible descriptions. If so, we need to carefully choose our groupings and descriptions of them.

A count variable counts the number of items or people in a specified time or place or occasion or group.

return to top

Identifying issues and planning

In the first part of the data investigative process, one or more questions or issues begin the process of identifying the topic to be investigated. In thinking about how to investigate these, other questions and ideas can tend to arise. Refining and sorting these questions and ideas along with considering how we are going to obtain data that is needed to investigate them, help our planning to take shape. A data investigation is planned through the interaction of the questions:

Example B: heights and spans

The general topic is investigating heights and spans and their difference in Year 5 students. What are possible issues of interest? Both the sizes and the variation of heights and spans across the class are of interest. Why would we be interested in the difference of span-height? Again both the general sizes and variation of the differences are of interest. Perhaps the students can think of other reasons, for example, to do with manufacture of clothing.

There are two measurements to be made on each student. Heights should be measured without shoes. The same way of measuring heights and spans should be followed carefully. There may be guidelines given on the web for measuring height. Why would this be so? Perhaps because height is such an important variable in monitoring growth. Would there be as much interest in span? If not, why not?

An example of how heights were used in the past in relation to ages of children can be found at http://old.rsscse.org.uk/qca/resource6.htm

Example D: number of shots in points in tennis

There is always at least one shot with the first serve. So if the first serve is in and is an ace, there is just one shot. If a serve is a fault, do we count it as one of the shots of the point? It does not lead to a rally but it is a shot in the point. What we decide to do depends to some extent on the reason for our interest. Are we investigating length of rallies or are we interested in the numbers of shots from the point of view of the amount of effort needed in tennis? If we do not count faults and lets, then it is possible to have observations of zero. If we do count total number of shots then we include faults and lets.

There can be many shots in a rally before the point is won. We would need to decide if we are interested in top players’ matches or in matches played by students learning to play tennis. We could collect a dataset for just one match or even one set of a match, or we could collect our data by recording the number of shots in points chosen at random. Different students or groups of students could choose different matches or parts of matches to record the numbers of shots.

If we choose to look at top players’ matches, do we look at men’s or women’s matches? Although in some tournaments, men play best of 5 and women best of 3, the number of points can vary considerably over both men’s and women’s matches, so students could choose a match they would like to investigate and compare their data with others.

Example E: time between shots at goal in soccer

As with the tennis example, students’ interest may be in top level soccer such as Australian A league or the English Premier League or in matches played in their age group or an older age group. Unlike the tennis example, and because the variable is time between shots at goal, focus will tend to be on data collected for a match. As with the tennis example, different students or groups of students could choose different matches and compare their datasets.

An important point here is to decide what is a shot at goal and to describe this carefully so that different students/groups of students collect data with a consistent definition of shot at goal. Because number of shots at goal is one of the summary statistics that is quoted for soccer matches, some guidelines on defining a shot at goal should be available, or possibly are already known by students who have started playing soccer.

Example I: count of the word 'Harry' per page

The interest in this example is not only how often the word 'Harry' tends to appear per page of a Harry Potter book, but also on how variable this is across pages. A practicality is to decide whether to count words such as 'Harry’s'. It is most unlikely that a word like Harry would be hyphenated or apostrophised across pages but if students do find this on any selected pages, they would seek guidance.

Example J: types of letterboxes

As with much categorical data, an issue in planning in this example is choosing and carefully describing the categories. For example, letterboxes could be classified by type of material, size, elaborateness etc. If material, they could be classified by their major material, for example, brick, wood, metal, other.

Another aspect for discussion or selection by the teacher is choice of region. This point is taken up below.

return to top

Collecting, handling and checking data

Example B: heights, spans and differences
for year 5 students

Apart from everyone being measured in the same way with shoes off, the only other questions in relation to collecting these data relate to desired precision of measurement. For example, is the same tape measure to be used? Should the same person take all the measurements? Should we measure to the nearest cm or to the nearest 0.5cm? For usual values of height and span for Year 5 students, the extra precision obtained through using the same tape measure and same person to measure may be unnecessary. Because the values of the differences (span-height) are not familiar, reasonable care may be needed to obtain accurate measurements of these, but the variation is likely to swamp minor inconsistencies in measurements.

The recording sheet is simple and the first few rows would look like the following.

Student
name 		Height
in cm 		Span
in cm 		Span − height
in cm
Abigail 136.5 cm 135.5 cm −1 cm
Fred 132 cm 134.5 cm 2.5 cm
Jenny 134.5 cm 136 cm 1.5 cm

Example D: number of shots to win a point in tennis

If it is decided to collect the data for all the points in a match or a set, then the data collection is simply a matter of accuracy and reporting which match/set. As this data collection is in real time, it is advisable for at least pairs of students to work together.

It is likely and probably easier to manage that students at this level will prefer to focus on a set or a match. They may ask how many points they should observe, and may think they need to observe the same number of points if different datasets are to be collected. This is not necessary, and observing all of a set with differing number of points could add to the interest in exploring the data.

If it is decided to choose points from across sets or even across matches, how to choose them at random is not necessarily straightforward. Use of random numbers by the teacher would be required, but as instructions based on any sequence produced is likely to cause confusion at this level, it may be best simply to allow students to choose in a way they think is 'random'.

The recording sheet is again simple and the first few rows would look like the following.

Point Number of shots
1 3
2 12
3 5

Example E: time between shots at goal

A suggestion is that students choose between this example and the above example on number of shots in a tennis point, or possibly similar data from another sporting context, but with collected data in each available to the rest of the class for exploring and discussion. For this example, because of the need to decide and describe what constitutes a shot at goal, it would be a good idea to do a pilot to make it easier for students to see and agree. The decision and description as to what constitutes a shot at goal, may be made as simple as desired to suit the level of the students.

It is advantageous to use a stopwatch if possible and to work cooperatively. However if using a stopwatch causes any problems, the times are simple to record when working in a pair or triple, and the times between can be obtained later. If recording the times at which shots at goal occurred, the first few lines of a recording sheet, starting at 2pm could look like the following. So that the times between are 10 mins, 2 mins, 8 mins.

Shot Time of shot
1 2.10pm
2 2.12pm
3 2.20pm

Example I: count of 'Harry' per page

Trying to choose the pages at random from a Harry Potter book, on which to count the number of occurrences of the word 'Harry' per page, can be a source of fun and discussion. Although random numbers could be used, the students’ choices of pages are likely to be just as 'random' from the point of view of number of occurrences of the word. As with all the above examples, the collection and recording is simple, with a recording sheet looking like:

Page Count of 'Harry'
5 7
43 15
49 5

Example J: types of letterboxes

The choice of region and organisation of collecting these data needs to be managed for safety reasons, avoiding of doubling-up of recording, and to obtain consistency in categorisation. Once students have decided and described their classifications of letterboxes, a small pilot will help in consistent classification. A recording sheet could look like:

Letterbox Type
2, Pumpkin Ct wood
4, Pumpkin Ct metal
6, Pumpkin Ct brick

General statistical notes for teachers

Each of the above examples demonstrates how planning a statistical investigation involves identification of the variables to be observed (what data are we going to collect) and the 'subjects' or 'experimental units' of the investigation − that is, on what we are going to collect or observe our variables?

But these examples also naturally introduce early notions of the question: of what are our data representative? With respect to heights, is our class representative of Australian Year 5’s? Of this age group 200 years ago? Of this age group in other countries? Is the tennis match or soccer match we chose representative of matches at that level? Is the region in which we looked at letterboxes representative of the city or a larger region?

return to top

Exploring and interpreting data

It is in exploring data that we use presentations, including graphical and summary presentations.

Categorical data are summarised by the number of observations that fall in each category. These are called the frequencies of the data − how often did each category occur. These frequencies can be presented in a table or can be graphed by a column graph in which each category has a column and the heights of the columns represent the frequency of the observations that fall in that category. Column graphs are also called barcharts.

Count data are also summarised by the number of observations that fall in each
category, where the categories correspond to the different possible count values that
the observations take. If most observations are for only a few different counts, but there are also a few large or unusual counts, these are sometimes grouped together in a category and the count data are treated as categorical (See examples in the module,
Data Investigation and Interpretation − Year 4)

Frequencies of categories or of count values are the numbers of observations in the data that fall into each category or that take each count value. It is frequencies that provide the information on how likely are the different categories or count values − which tend to occur more frequently and which tend to occur less frequently.

Measurement data can be presented by dotplots. A dotplot plots quantitative data, with a dot on the graph for each value in the set of quantitative data. If a value occurs 3 times, there are 3 dots in a line above that value. Hence the heights of the columns of dots give the frequencies of the data values. If there are many observations in the dataset, each dot might represent two or three observations. For measurement data, a dotplot is a plot of the 'raw' data with no grouping of values. So if a set of measurement values is not large and has many different values, a dotplot is not very informative, but a dotplot is usually an excellent way to have a first look at data. Count data can also be represented by a dotplot.

Dotplots are easily done by hand and are also available in most statistical software.

General statistical notes for teachers

Measurement data are observed in units of measurement and are recorded correct to some unit of measurement. In this module, we just see simple plots of frequencies of the different values observed in the data, but in later modules we see that measurement data values are actually small intervals. For example, 'the boy has a height of 140cm' is more correctly said as 'the boy has a height between 139.5 and 140.5 cm'

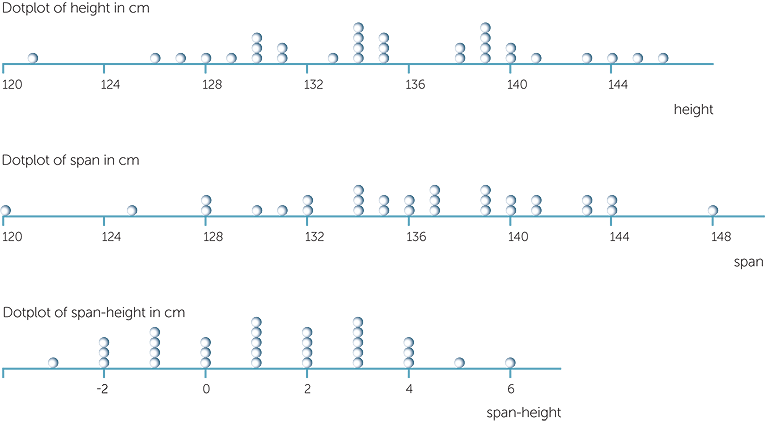
Example B: heights, spans and span-height

Below are some dotplots of height, span and span-height (all in cm) for 30 Year 5 students. The dotplots show that both the heights and the spans vary from about 120 cm to 146cm in height and 148 cm in span. So these plots indicate that the spans and heights may be close to similar. The dotplot of span-height shows that students’ spans vary from 3cm less than height up to 6 cm more than their height, with more students having their spans slightly greater than their heights.

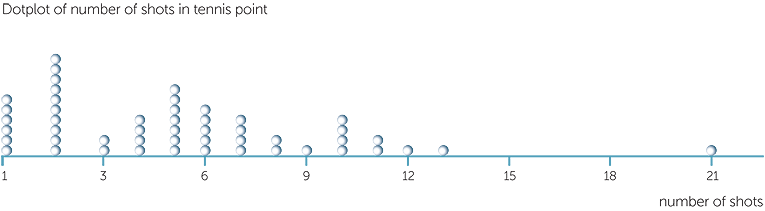
Example D: number of shots to win a point in tennis

Below is a dotplot of the number of shots in each point in a set of tennis. We see that there were 6 points that were won with an ace on the first serve, and that even more points were won with just two shots − so either a fault and then an ace or a first serve in and then a winning return. If the number of shots went beyond two, there tended to be at least a few more shots, and in some cases many more, before the point ended.

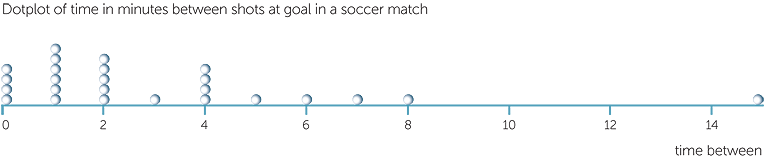
Example E: time between shots at goal in soccer

Below is a dotplot of the time in minutes between shots at goal in a soccer match. Because the times are rounded to the nearest minute, there are 4 that have been rounded to 0 − these were probably 'second' or 'third' rebound shots within the goal square. There are quite a few low times and a small number of greater times with one of 15 minutes.

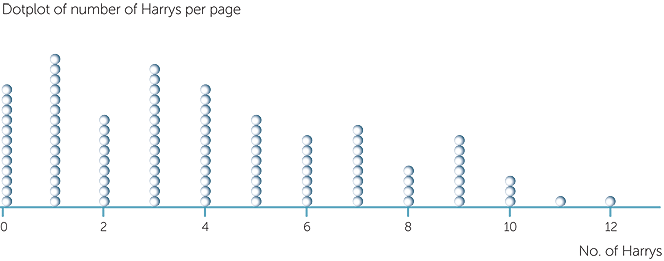
Example I: number of Harrys per page

Below is a dotplot of the numbers of Harrys per page from 100 pages chosen randomly from a Harry Potter book. Most of the pages have low numbers of Harrys, but, like the datasets above on numbers of shots in tennis points and time between shots at goal in soccer, there are some pages with 6 to 12 occurrences of the word 'Harry'.

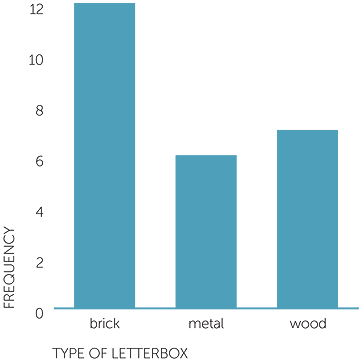
Example J: types of letterboxes

This is categorical data so a column graph is the appropriate graph. Below is a column graph of 27 letterboxes classified by their main material. Brick was the most common material, with metal and wood occurring in similar frequencies to each other.

graph of type of letterbox

return to top

Some general comments and links
from F-4 and towards year 6

As in Year 4, although the focus is on considering just one variable at a time, the above examples again illustrate the extent of statistical thinking involved in the initial stages of an investigation in identifying the questions/issues and in planning and collecting the data. The above examples also show that at least some indications of concepts of 'what do our data represent' and variation in data across samples, tend to arise naturally in everyday situations that are very familiar to young students.

The examples here focus on a measurement, count or categorical variable and consider two types of graphs. Measurement variables are continuous variables (they take values in intervals); count and categorical variables are discrete variables (they take separated values). The word 'continuous' should be used as students progress to the higher years.

Dotplots are for quantitative data and column graphs are for categorical data. Both types of graphs show the frequencies of the different values in the dataset, but the distances between ticks along the x-axis in a dotplot are quantitative and meaningful, whereas the arrangement of categories along the x-axis in a column graph is arbitrary and the distances between the columns have no meaning. Column graphs are sometimes used for count data with only a few different values, but usually to use column graphs for count data, the count data need to be converted to categorical data with the last category being 'more than …'. The examples above show how information can be lost in many situations by such grouping.

Although some of the examples in Year 5 involve more than one variable and the motivating questions do in fact include, or teeter on including, comparisons of data for one variable across categories of another categorical variable, such comparisons have been only lightly touched on. In Year 6 we restrict attention again to categorical variables, but start considering the possibility of association between variables. Does the behaviour of one of the variables depend on the other?

 

The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.

The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.

© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/

Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.

AMSI ICE-EM