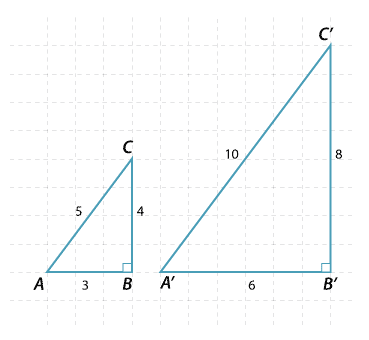Content description

Use similarity to investigate the constancy of the sine, cosine and tangent ratios for a given angle in right-angled triangles (ACMMG223)

Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)

Similarity of right-angled triangles

The triangles pictured are similar (SSS), that is the corresponding sides are in the same ratio. Hence the matching angles are the same.

Detailed description

For any right-angled triangle similar to triangle ABC, the ratio of the matching sides will be the same.

\begin{align}\dfrac{BC}{B^\prime C^\prime}=\dfrac{CA}{C^\prime A^\prime}=\dfrac{AB}{A^\prime B^\prime}=\dfrac{2}{1}\end{align}

Notice that we can also write

\begin{align}\dfrac{BC}{CA}=\dfrac{B^\prime C^\prime}{C^\prime A^\prime}=\dfrac{4}{5}, \ \dfrac{BC}{AB}=\dfrac{B^\prime C^\prime}{A^\prime B^\prime}=\dfrac{4}{3} \ \text{and} \ \dfrac{CA}{AB}=\dfrac{C^\prime A^\prime}{A^\prime B^\prime}=\dfrac{5}{3}\end{align}

That is, once the angles of a triangle are fixed, the ratios of the sides of the triangle are constant. In a right-angled triangle, we only need to know one other angle and then the angle sum of a triangle gives us the third angle. Hence, in a right-angled triangle, if we know one other angle, then the ratios of the sides of the triangle are constant.

This is the basis of trigonometry.