![]()
Finding angles
Example 2
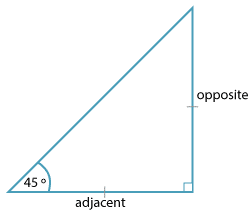
This is an isosceles right angled triangle and tan 45° = 1.
We can say that is the inverse tangent of 1.
We write tan\(^{−1}\)1 = 45°.
Similarly,
sin\(^{−1}\) 0.5 = 30° as sin 30° = 0.5.
A calculator give cos 27° = 0.8910 (correct to 4 decimal places) and so:
cos\(^{−1}\) 0.8910 \(\approx\) 27°.
We read sin\(^{−1} \ x\) as inverse sine of \(x\) and cos\(^{−1}\ x\) as inverse cosine of \(x\).
Example 3
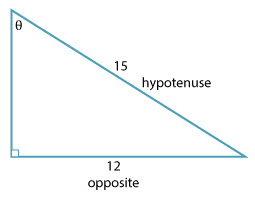
Find the value of \(\theta\) correct to the nearest degree.
Solution
This problem involves opposite and hypotenuse so use sine.
\begin{align}\text{sin} \ \theta \ &= \ \dfrac{12}{15} \\ &= \ \dfrac{4}{5} \\ \theta &= \ \text{sin}^{–1}(\dfrac{4}{5}) \\ &\approx 53.1301° \ (\text{correct to} \ 4 \ \text{decimal places}) \\ &\approx 53° \ \text{to the nearest degree}.\end{align}