Special angles
The angles 30°, 45° and 60° appear frequently in trigonometry and their sine, cosine and tangent ratios can be expressed using rational numbers and surds.
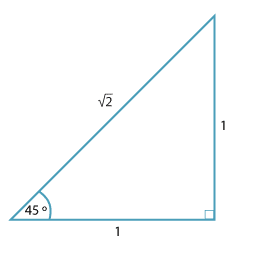
The value of the trigonometric ratios for 45° can be found from the diagram below. It is an isosceles triangle with shorter sides 1.
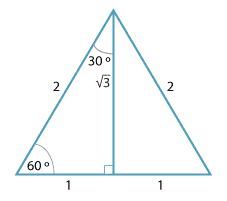
The value of the trigonometric ratios for 30° and 60° can be found from the diagram below.
It is an equilateral triangle of side length 2, with the bisector of one angle drawn.
The values are given in the table below
| \(\theta\) | sin \(\theta\) | cos \(\theta\) | tan \(\theta\) |
|---|---|---|---|
| 30° | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{1}{\sqrt{3}}\) |
| 45° | \(\dfrac{1}{\sqrt{2}}\) | \(\dfrac{1}{\sqrt{2}}\) | 1 |
| 60° | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{1}{2}\) | \(\sqrt{3}\) |
Students need to either learn the table or remember the triangles to construct the table.
By complementary angles, note that sin 60° = cos 30°, cos 60° = sin 30°, and sin 45° = cos 45°.
In fact it is always the case that cos (90° – \(\theta\)) = sin \(\theta\) and sin (90° – \(\theta\)) = cos \(\theta\), where \(\theta\) is measured in degrees. This can be seen by drawing a triangle, marking the reference angle as \(\theta\)°, and then the remaining acute angle as 90° – \(\theta\)°.
  |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Terms of use  |
