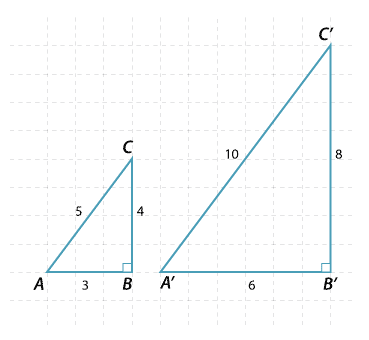The triangles pictured are similar (SSS), that is the corresponding sides are in the same ratio. Hence the matching angles are the same.

Detailed description

For any right-angled triangle similar to triangle ABC, the ratio of the matching sides will be the same. It doesn’t matter what the size of the right angled triangle, the ratio of the matching sides will be the same.

\begin{align}\dfrac{BC}{B^\prime C^\prime}=\dfrac{CA}{C^\prime A^\prime}=\dfrac{AB}{A^\prime B^\prime}=\dfrac{2}{1}\end{align}

Notice that we can also write

\begin{align}\dfrac{BC}{CA}=\dfrac{B^\prime C^\prime}{C^\prime A^\prime}=\dfrac{4}{5}, \ \dfrac{BC}{AB}=\dfrac{B^\prime C^\prime}{A^\prime B^\prime}=\dfrac{4}{3} \ \text{and} \ \dfrac{CA}{AB}=\dfrac{C^\prime A^\prime}{A^\prime B^\prime}=\dfrac{5}{3}\end{align}

Once the angles are fixed, the ratios of the sides are constant.