Volume of cylinders

Cylinders are ubiquitous in everyday life. For example tinned food normally comes in a can whose shape is a cylinder.

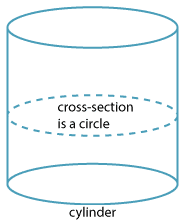
If we slice a cylinder parallel to its base, then each cross-section is a circle of the same size as the base.

Thus a cylinder has the same basic property as a prism, and we will take the formula for the volume of a cylinder to be the area of the circular base times the height. We cannot prove this formula rigorously at this stage, because the proof involves constructing the cylinder as a limit of prisms.

If the base circle of the cylinder has radius r, then we know that the area of the circle is A = πr². If the height of the cylinder is h, then its volume is:

Volume of a cylinder = Ah = πr²h.

 

Example 5

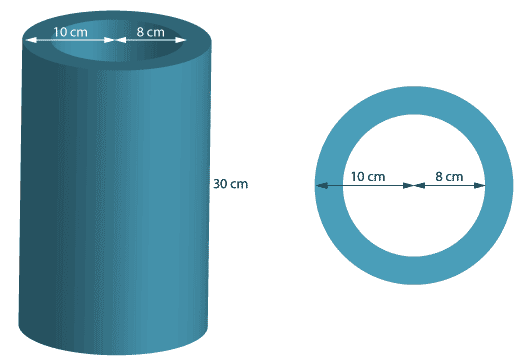
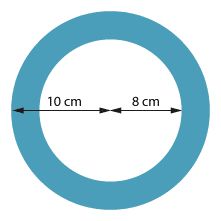
A thermos flask of height 30 cm is in the shape of two cylinders, one inside the other. It has an inner radius of 8 cm and an outer radius of 10 cm. What is the volume between the two cylinders?

Detailed description

Solution method 1

The volume between the cylinders will be the difference in volume.

\begin{align}\text{Volume of the outer cylinder} &= \text{area of the base}\ ×\ \text{height}\\ &= π × 10^2 × 30\\ &= 3000 π\ \text{cm³}.\\ \text{Volume of the inner cylinder}\ &= π × 8^2 × 30\\ &= 1920π\ \text{cm³}.\\ \text{Hence the volume between the cylinders}\ &= 3000π\ – 1920π\\ &= 1080π\ \text{cm³}\\ &\approx 3392.92\ \text{cm³ (correct to two decimal places)}.\end{align}  

Solution method 2

\begin{align}\text{Volume}\ &= \text{area of the base × height}\\ \text{Area of the base}\ &= \text{area of the annulus pictured}\end{align}

Detailed description

\begin{align}\text{Area}\ &= π × 10^2\ –\ π × 8^2\\ &= π × (10^2\ –\ 8^2 )\\ &= π × (100\ –\ 64)\\ &=36π\ \text{cm²}.\\ \text{Hence volume}\ &= 36π × 30\\ &=1080π\ \text{cm³}\\ &\approx 3392.92\ \text{cm³ (correct to two decimal places)}.\end{align}