![]()
Surface area of cylinders
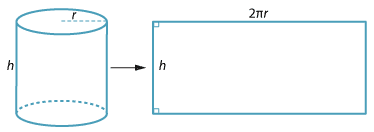
Consider a cylinder with base radius r and height h. If we roll it along a flat surface through one revolution as shown, the curved surface traces out a rectangle of width the height of the cylinder and length the circumference of the circle.
\begin{align}\text{Circumference of a circle} &= 2πr\\ \text{Area of the curved surface of a cylinder} &= 2πrh\\ \text{Area of a circle} &= πr²\end{align}Example 3
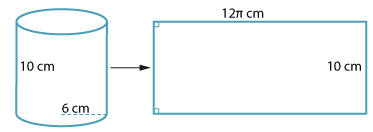
Calculate the surface area of the cylinder with height 10 cm and base radius 6 cm.
Solution
and

Work in terms of π and only approximate at the last step.