Volumes of other solids with constant cross-section

The volume of any solid with constant cross-sectional area can be found by using the same formula:

Volume = Ah where A is the area of the base and h is the height.

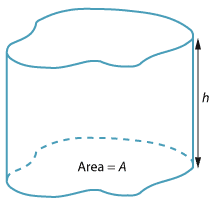
Ensure that the base, the constant cross-sectional area, is identified first as the objects are not necessarily lying on their base.

Example 3

Find the volume of the shape pictured.

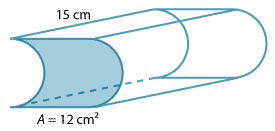
Solution

\begin{align}V &= A h\\ &= 12 × 15\\ &= 180\ \text{cm³}.\end{align}  

Example 4

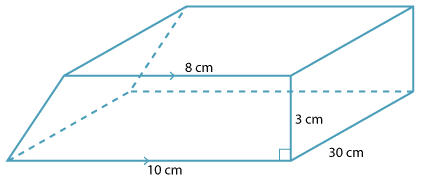
Find the volume of the solid pictured.

Detailed description

Solution

The cross sectional area (base) is the trapezium face.

\begin{align}A &= \dfrac{1}{2} × 3 × (8 + 10)\\ &= 27\ \text{cm²}\\ h &= 30\ \text{cm}\\ V &= Ah\\ &= 27 × 30\\ &= 810\ \text{cm³}.\end{align}