Example 2

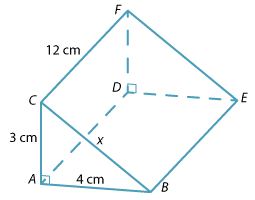
Calculate the surface area of the triangular prism pictured.

Detailed description

Solution

This prism has the measurements as shown. In order to calculate the area of the top rectangular face, we need to use Pythagoras' theorem to calculate the length of the hypotenuse of the base triangle.

By Pythagoras' theorem in \(\triangle ABC\):

\begin{align}x² &= 3² + 4²\\ &= 25\\ x &= \sqrt{25}\\ &= 5\end{align}

The surface area is comprised of:

\begin{align}\text{Two triangles with area} \dfrac{1}{2} × 3 × 4 &= 6\ \text{cm²}\\ \text{One rectangle with area}\ 5 × 12 &= 60\ \text{cm²}\\ \text{One rectangle with area}\ 3 × 12 &= 36\ \text{cm²}\\ \text{One rectangle with area}\ 4 × 12 &= 48\ \text{cm²}.\end{align}

So the surface area of the triangular prism is 2 × 6 + 60 + 36 + 48 = 156 cm².