![]()
Gradient of an interval
The gradient is a measure of the steepness of a line. There are several ways to measure steepness. In coordinate geometry the standard way to define the gradient of an interval AB is \(\dfrac{rise}{run}\) where rise is the change in the y-values as you move from A to B and run is the change in the x-values as you move from A to B. We will use the pronumeral m for gradient.
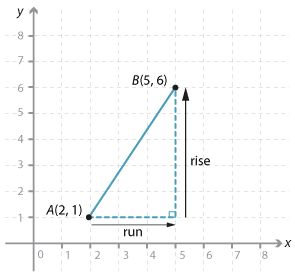
Given the points A(2, 1) and B(5, 6):
Gradient of the line interval \(AB = \dfrac{rise}{run} =\ \dfrac{6 - 1}{5 - 2} =\ \dfrac{5}{3}\).
Notice that as you move from A to B along the interval the y-value increases as the x-value increases. The gradient is positive.
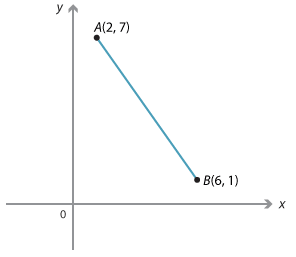
Given the points A(2, 7) and B(6, 1):
Gradient of the line interval \(AB =\dfrac{rise}{run}=\dfrac{1 - 7}{6 - 2}=\dfrac{-6}{4}=-\dfrac{3}{2}\)
or
Gradient of interval \(BA =\dfrac{rise}{run}=\dfrac{7 - 1}{2 - 6}=-\dfrac{3}{2}.\)
Notice that in this case the y-value decreases as the x-value increases. The gradient is negative.
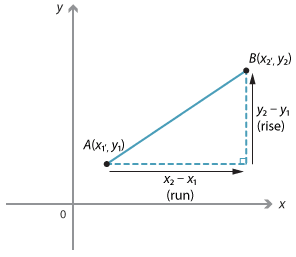
General gradient of an interval
\begin{align}\text{Gradient of line interval}\ AB &= \dfrac{rise}{run}\\\\ m &= \dfrac{y_2 - y_1}{x_2 - x_1}.\end{align}Note that since \(\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{y_2 - y_1}{x_2 - x_1}\) it does not matter which point we take as the first and which point we take as the second.
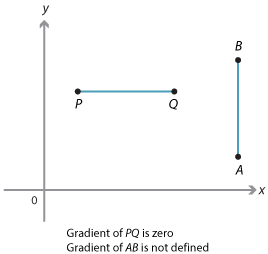
If the interval is vertical, the run is zero
and the gradient of the interval is not
defined. This is shown by interval AB.
If the interval is horizontal, the rise is zero
as shown by interval PQ. The gradient of
the interval is zero.