![]()
The midpoint of an interval
The coordinates of the midpoint of a line interval can be found using averages as we will see.
We first deal with the situation where the points are horizontally or vertically aligned.
Example 1
Find the coordinates of the midpoint of the line interval AB, given the following points:
- \(A(1, 2)\) and \(B(7, 2)\)
- \(A(1, −2)\) and \(B(1, 3)\)
Solution
- AB is a horizontal line interval, the midpoint is at (4, 2), since 4 is halfway between 1 and 7.
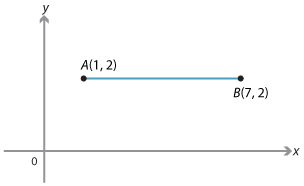
Note that 4 is the average of 1 and 7, that is: 4 = \(\dfrac{1 + 7}{2}\). - The midpoint of AB has coordinates \((1, \dfrac{1}{2})\).
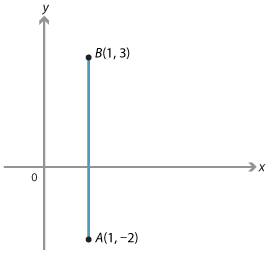
Note that \(\dfrac{1}{2}\) is the average of 3 and \(-2\).




