![]()
Variability
To investigate further, thirty samples of 30 balls are taken and the number of red balls in each sample is recorded.
| 8 | 9 | 9 | 11 | 10 | 11 | 6 | 12 | 10 | 14 | 11 | 14 | 9 | 9 | 12 |
| 12 | 12 | 7 | 10 | 13 | 5 | 9 | 10 | 12 | 10 | 11 | 10 | 10 | 8 | 6 |
This is summarised in the table below.
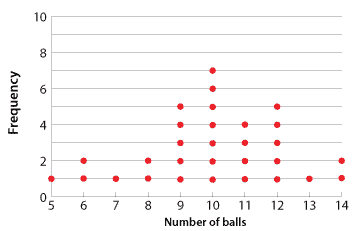
| Number of red balls | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | 1 | 2 | 1 | 2 | 5 | 7 | 4 | 5 | 1 | 2 |
So, we can see that 9 red balls were obtained from five of the samples, 10 from seven of the samples and so on.
We can represent these results in a dot plot, as shown below.
Detailed description
Now we can look at the frequency of each proportion (relative frequency), shown below.
| Proportion of red balls | 25% | 30% | 35% | 40% | 45% | 50% | 55% | 60% | 65% | 70% |
|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | 1 | 2 | 1 | 2 | 5 | 7 | 4 | 5 | 1 | 2 |
So, we can see that the sample proportion of red balls varies greatly, from 25% to 70%. At this stage, we have no method for determining the limitations of our estimate.
There is always variability in the proportion with random sampling. More work will need to be done before the relative frequency can be used in any way to estimate the number of red balls in the bin.




