Example 1

Find the circumference of a circle:

1. whose diameter is 14 cm
2. whose radius is 21 cm.

Give each answer:

1. in terms of π
2. as an approximate value, using π ≈ \(\dfrac{22}{7}\)
3. as an approximate value using π ≈ 3.14.

Solution

\begin{align}{\bf \text{a i}}\hspace{20px} C &= \pi d\\\\&= 14\pi\ \text{cm}\end{align}	\begin{align}{\bf \text{a ii}}\hspace{15px} C &= 14\pi\\\\&\approx 14 ×\dfrac{22}{7}\\\\&= 44\ \text{cm}\\\\\end{align}	\begin{align}{\bf \text{a iii}}\hspace{10px} C &= 14\pi\\\\&\approx 14 × 3.14\\\\&= 43.96\ \text{cm}\end{align}
\begin{align}{\bf \text{b i}}\hspace{20px} C &= 2\pi r\\\\&= 2 × \pi × 21\\\\&= 42\pi\ \text{cm}\end{align}	\begin{align}{\bf \text{b ii}}\hspace{15px} C &= 42\pi\\\\&\approx 42 ×\dfrac{22}{7}\\\\&= 132\ \text{cm}\end{align}	\begin{align}{\bf \text{b iii}}\hspace{10px} C &= 42\pi\\\\&\approx 42 × 3.14\\\\&= 131.88\ \text{cm}\end{align}

Note that the answers in parts ii and iii are only approximate, since we have used an approximation for π.

Example 2

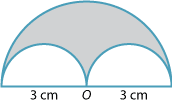
The figure is obtained by removing the two semicircles from the large semicircle. What is the exact perimeter of the shaded region?

Detailed description

Solution

This perimeter consists of half the circumference of the large circle (a semicircle) plus two small semicircles, or one whole small circle.

Radius of large circle = 3 cm

Radius of small circles = 1\(\dfrac{1}{2}\) or \(\dfrac{3}{2}\) cm

Hence the perimeter = \(\pi × 3 + 2 × \pi × \dfrac{3}{2} = 6\pi\) cm

Example 3

A circle has circumference 50π cm. Find the radius of the circle.

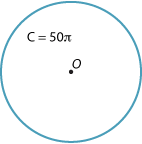
Solution

\begin{align}\text{Circumference}\ &= 2\pi r\\\\ 2\pi r &= 50\pi\\\\ r &=\dfrac{50\pi}{2\pi}\\\\ &= 25\ \text{cm}\end{align}