The formula for area of a circle

The dissections shown above strongly suggest that the correct formula for the area of a circle with radius r is

A formal proof of this result requires an understanding of the concept of limits, which will be studied in senior mathematics.

Example 1

1. Find the area of a circle whose radius is 7 cm.
2. Find the area of a circle whose diameter is 7 cm.

Give each answer:

1. in terms of π
2. as an approximate value, using \(\pi \approx \dfrac{22}{7}.\)

Solution

\begin{align}{\bf \text{a i}}\hspace{22px} A &= \pi r^2\\\\ &= 49\pi\ \text{cm}^2\end{align} \begin{align}{\bf \text{a ii}}\hspace{18px} A &= 49\pi\\\\ &\approx 49 × \dfrac{22}{7}\\\\ &= 154\ \text{cm}^2\end{align}

b i Since the diameter is 7 cm, the radius is \(\dfrac{7}{2}\ \text{cm}\)

\begin{align}{\bf \text{b ii}}\hspace{18px} A &=\dfrac{49}{4}\pi\\\\ &\approx \dfrac{49}{4} × \dfrac{22}{7}\\\\ &=38\dfrac{1}{2}\ \text{cm}^2\end{align}

Example 2

A circle has area \(1386\ \text{cm}^2.\) Using \(\pi \approx\dfrac{22}{7},\) find the approximate value of the radius.

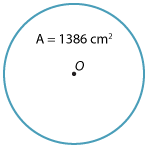
Solution

\begin{align}A &= \pi r^2\\\\ \pi r^2 &= 1386\\\\ r^2 &= \dfrac{1386}{\pi}\\\\ &\approx 1386 ÷\dfrac{22}{7} \\\\ &\approx \dfrac{1386}{1}× \dfrac{7}{22} \\\\ &= 441\\\\ r &= \sqrt{441}\\\\ &= 21\ \text{cm}\end{align}

Example 3

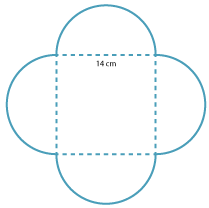
Four semicircles are drawn along the edge of a square with side length 14 cm.

1. Find the area of the entire region, giving your answer in terms of π.
2. Find the approximate value of the area, using \(\pi \approx \dfrac{22}{7}\) .

Solution

1. Area region = area of the square + 2 × area of the circle
   \begin{align}\text{Area square} &= 14 × 14\\\\ &= 196\ \text{cm}^2\end{align} \begin{align}\text{Radius of circle} &= 7\ \text{cm}\end{align} \begin{align}\text{Area of circles} &= 2 × \pi × 7^2\\\\ &= 2 × \pi × 49\\\\ &= 98\pi\ \text{cm}^2\end{align} Hence the area of the region = (196 + 98π) cm\(^2\)
2. \begin{align}\text{Area} &≈ 196 + 98 × \dfrac{22}{7}\\\\ &= 196 + 308\\\\ &= 504\ \text{cm}^2\end{align}