Area of circles

We know that the area of a rectangle, with sides of lengths l and w, is calculated by the formula A = lw. We then used this formula, together with dissection arguments, to find the area of other figures bounded by straight lines.

The ancient Greek mathematician Archimedes came up with a number of clever ways to find a formula for the area of a circle in terms of the radius. The Greeks discovered that if you double the radius of a circle, then the area is increased by a factor of four. If you triple the radius, then the area increases by a factor of nine. They concluded that the area of a circle seemed to be related to the square of the radius.

Here we describe two ways to find the area of a circle.

Dissection using concentric circles

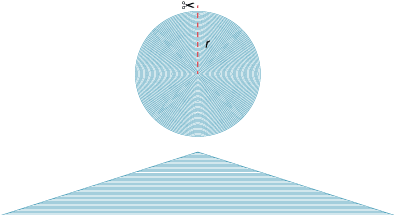
Imagine that a circle of radius r is made up of a large number of concentric circular pieces of very thin string. The circles are then cut along a radius, and the pieces of string are straightened out and laid one on top of the other as shown in the diagram below to form a shape that is approximately a triangle. The thinner the pieces of string, the closer we come to a triangle.
The base of the triangle is the circumference of the circle, πd or 2πr and the height of the triangle is the radius r of the original circle.

Hence the area inside the circle is approximately the area of the triangle:

\begin{align}\text{Area}\ = \dfrac{1}{2} × \text{base} × \text{height} &= \dfrac{1}{2} × 2\pi r × r\\\\ &= \pi r^2\end{align}

Dissection by sectors

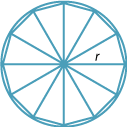
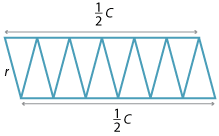
The second way of finding the area is to dissect the circle into sectors, just as you would a pizza. These sectors can then be arranged alternately, as in the diagram below, to form a shape that is approximately a rectangle whose width is r and whose length is half the circumference, that is, πr, The smaller the sectors, the closer the shape is to being a rectangle. Thus the area is approximately:

\begin{align}\text{Area}\ = \text{length} × \text{width} &= \pi r × r\\\\ &= \pi r^2\end{align}

Detailed description