Definition of a circle

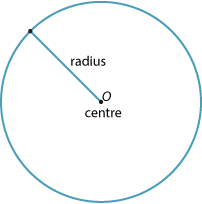
A circle is the path traced out by a point, moving in a plane, that is always a fixed distance (the radius) from a fixed point (the centre).

Parts of the circle

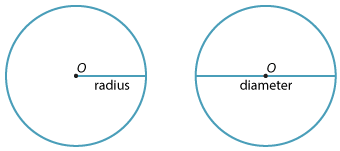
Any interval (or line segment) drawn from the centre of a given circle to any point on the circle is called a radius (plural radii).

Any interval joining two points on the circle and passing through the centre is called the diameter of the circle.

Detailed description

Because every radius has the same length and every diameter has the same length, we often use the words 'radius' and 'diameter' to refer to either the interval in question or the length of that interval. Thus the diameter of a circle is twice the radius of that circle.

A diameter divides the circle into two congruent parts. Each part is called a semicircle. If we draw a radius perpendicular to the diameter in a semicircle, we obtain two congruent quadrants.

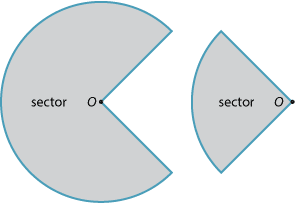
Any two radii divide the circle into two pieces. Each piece is called a sector (from the Latin word secare − to cut).

Features of the circle

• A circle is formed by all points that lie a fixed distance r from a fixed point O.
• Any interval drawn from the centre to a point on the circle is called a radius of the circle.
• Any interval joining two points on the circle and passing through the centre is called a diameter of the circle.
• A diameter divides the circle into two equal parts. Each part is called a semicircle.
• If a radius is drawn cutting a semicircle into two equal parts, then each part is called a quadrant.
• Any two radii divide the circle into two pieces. Each piece is called a sector.