The RHS congruence test

We have seen that two sides and a non-included angle are, in general, not enough to determine a triangle up to congruence. When the non-included angle is a right angle, however, we do obtain a valid test. In this situation, one of the two specified sides lies opposite the right angle, and so does the hypotenuse.

The test is therefore given the initials RHS for 'Right angle', 'Hypotenuse, 'Side'.

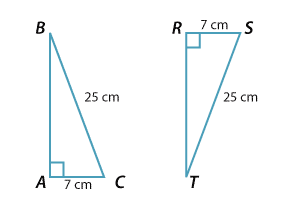
Here \(\triangle ABC \equiv \triangle RTS\). Any right-angled triangle with hypotenuse of length 25 cm and one other side of length 7 cm is congruent to triangle \(ABC\).