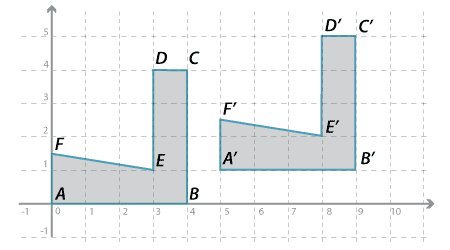
Two plane figures are called congruent if one can be moved by a sequence of translations, rotations and reflections so that it fits exactly on top of the other figure.
The example above involves a translation of 5 to the right and 1 up. The two hexagons are congruent.
In the second diagram the second hexagon has been obtained from the first by a rotation of 270 ° clockwise about \(B\) and then a translation of 1 unit to the right. Note that the orientation of the shape has not changed. Once again, the two hexagons are congruent.
  |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Terms of use  |
