The SSS congruence test

• If the three sides of one triangle are respectively equal to the three sides of another, then the two triangles are congruent.
• If we are given the lengths of the three sides of a triangle, then only one such triangle can be constructed up to congruence.

The initials SSS stand for 'Side', 'Side', 'Side'.

You need to be given three side lengths of a triangle (two is not enough) to be able to construct a triangle that is unique up to congruence.

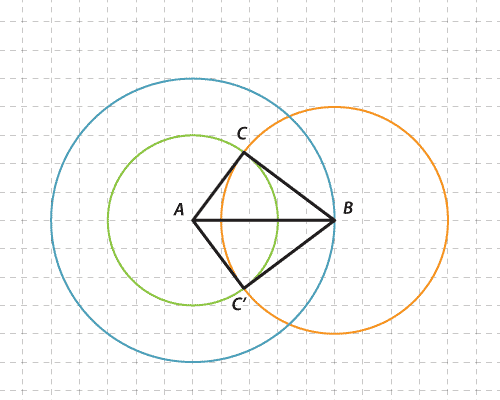
A three-sided triangle is constructed in the following stages.

• A blue circle with the centre A and with a radius of 5 units is drawn.
• Point B is marked on this circle.
• An orange circle with the centre B and a radius of 4 is drawn.
• A green circle with a radius of 3 and the centre A is drawn.
• The green and orange circles intersect at C and C′.

Detailed description

This method can be used for constructing any triangle where three lengths have been given. (The sum of the two shortest lengths must be greater than the third length for the triangle to exist.)