![]()
The real numbers and the rational numbers
We have seen that as we place halves, thirds, quarters, fifths, \(\ldots\) on the number line, the maximum gap between successive fractions tends to zero. Thus if α is any real number then rational numbers can be placed increasingly close to α. Thus we can use rational numbers to approximate a real number correct to any required order of accuracy.
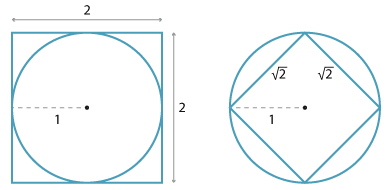
For example, the diagrams above show a circle of area \(\pi\) enclosed in a square of area 4, and enclosing a square of area 2, which proves that 2 < \(\pi\) < 4.
Archimedes improved greatly on this result by using regular polygons with 96 sides, and was able to prove that \(3\dfrac{10}{71}<\pi<3\dfrac{1}{7}\).