![]()
Constructing real numbers
Rational numbers
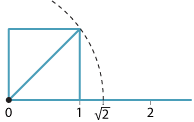
We know that every rational number can be plotted on the number line.
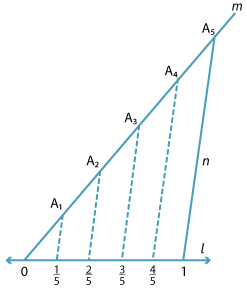
Here is an example illustrating the construction of \(\dfrac{1}{5}, \dfrac{2}{5}, \dfrac{3}{5} \text{and} \dfrac{4}{5}\).
Starting with 0 and 1 on l, draw any line m through 0 (m ≠ l).
Choose a point A1 on m, (A1 ≠ 0).
With a compass construct equally spaced points 0, A1, A2, A3, A4 and A5 on m.
Join A5 to 1 − call this line n.
Finally, construct four lines parallel to n through A1, A2, A3, A4 meeting l at four points.
These points on l are equally spaced, so we have constructed \(\dfrac{1}{5}, \dfrac{2}{5}, \dfrac{3}{5} \text{and} \dfrac{4}{5}\) on the line l.
Irrational numbers on the number line
We can place the square root of any whole number on the number line using Pythagoras'
theorem.
For example, to plot \(\sqrt{2}\) we first construct a
square on the interval from 0 to 1. Then we draw the diagonal from 0, which has
length \(\sqrt{2}\), and use compasses to place this length
on the number line.
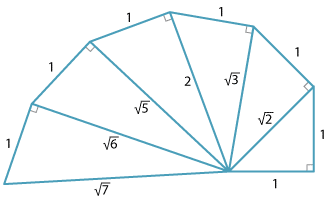
Other surds and Pythagoras
The diagram illustrates how the square roots of some other integer values can be constructed. Using the same methods as above, these irrational numbers can be placed on the number line.