Constructing real numbers

Rational numbers

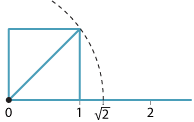
We know that every rational number can be plotted on the number line.
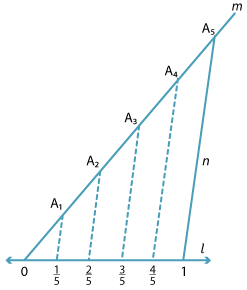
Here is an example illustrating the construction of \(\dfrac{1}{5}, \dfrac{2}{5}, \dfrac{3}{5} \text{and} \dfrac{4}{5}\).
Starting with 0 and 1 on l, draw any line m through 0 (m ≠ l).
Choose a point A₁ on m, (A₁ ≠ 0).
With a compass construct equally spaced points 0, A₁, A₂, A₃, A₄ and A₅ on m.
Join A₅ to 1 − call this line n.
Finally, construct four lines parallel to n through A₁, A₂, A₃, A₄ meeting l at four points.
These points on l are equally spaced, so we have constructed \(\dfrac{1}{5}, \dfrac{2}{5}, \dfrac{3}{5} \text{and} \dfrac{4}{5}\) on the line l.

Irrational numbers on the number line

Detailed description

We can place the square root of any whole number on the number line using Pythagoras' 
theorem.
For example, to plot \(\sqrt{2}\) we first construct a 
square on the interval from 0 to 1. Then we draw the diagonal from 0, which has 
length \(\sqrt{2}\), and use compasses to place this length 
on the number line.

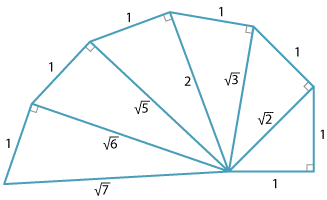
Other surds and Pythagoras

The diagram illustrates how the square roots of some other integer values can be constructed. Using the same methods as above, these irrational numbers can be placed on the number line.

Detailed description