The real numbers

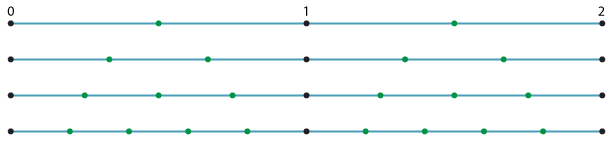
Think about graphing the rational numbers between 0 and 2 on the number line. First we graph \(\dfrac{1}{2},\) 1\(\dfrac{1}{2},\) then the thirds, then the quarters, then the fifths, \(\ldots\). As we keep going, the gaps between the dots get smaller and smaller.

Detailed description

If we imagine the situation when all the infinitely many rational numbers have been graphed, there appears to be no gaps at all, and the rational numbers are spread out like pieces of dust along the number line. Surely every point on the number line has been accounted for by some rational number?

Not true! There are infinitely many numbers that we have not graphed, all rational multiples of \(\sqrt{2}\), including:

\(\sqrt{2},\ \dfrac{1}{2}\sqrt{2},\ \dfrac{1}{3}\sqrt{2},\ \dfrac{1}{4}\sqrt{2},\ \text{and} \dfrac{1}{5}\sqrt{2}\)

Of course, there are many more missing numbers, like \(\sqrt{2}\) and log\(_2\) 3 and \(\dfrac{\pi}{2}.\) We need a new definition of 'numbers' that will cover all these irrational objects, which are not rational numbers, but which we nevertheless want to think of as numbers. The solution is very simple – we make an appeal to geometry and define numbers using the geometrical idea of points on a line.

Definition

The real numbers are all of the points on the number line.

The set of real numbers consists of both the rational numbers and the irrational numbers.