![]()
Equations of lines
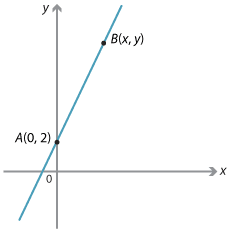
Consider the line with gradient 3 and y-intercept 2. This passes through the point A(0, 2). Let B(x, y) be any point on this line.
\begin{align}\text{Gradient of interval}\ AB &= \dfrac{rise}{run}\\ &= \dfrac{y − 2}{x − 0}\\ &= \dfrac{y − 2}{x}\end{align}The gradient of the line is 3.
\begin{align}\text{So} \dfrac{y − 2}{x}&= 3\\ \text{Rearranging} y − 2 &= 3x\\ y &= 3x + 2\end{align}So the coordinates of B(x, y) satisfies y = 3x + 2. This is called the equation of the line.
Conversely, suppose that B(x, y) satisfies the equation y = 3x + 2, then \(\dfrac{y − 2}{x − 0}\) = 3 and it passes though the point (0, 2) so the point lies on the line with gradient 3 and y-intercept 2.
We summarise this by saying that the equation of the line is y = 3x + 2.