Example 1

1. The graph of the line with equation y = 2x + 1.
   The y-intercept is 1 and the gradient = \(\dfrac{2}{1}\) = 2.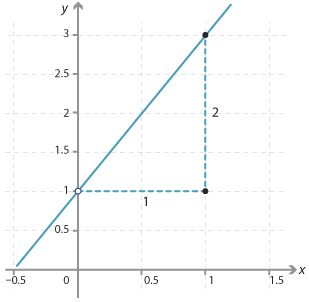
   
   Detailed description
2. The graph of the line with equation \(y=−2x+1.\)
   The y-intercept is 1 and the gradient \(y=\dfrac{−2}{1}=−2.\)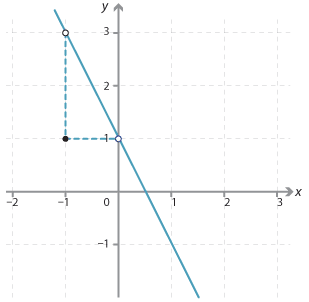
   
   Detailed description

In summary

Equations of the form y = mx + c

The graph of each equation is a straight line, m is the gradient of the line and c is the y-intercept. Conversely, if a straight line has gradient m and y-intercept c it has equation y = mx + c.

Example 2

Write down the gradient and y-intercept of the lines and state which way each slopes:

1. y = 9x + 2
2. y = −x + 8

Solution

1. The gradient is 9. The y-intercept is 2. The gradient is positive so the line slopes up from left to right.
2. The gradient is −1. The y-intercept is 8. The gradient is negative so the line slopes down from left to right.

Solution

1. The gradient is 9. The y-intercept is 2. The gradient is positive so the line slopes up from left to right.
2. The gradient is −1. The y-intercept is 8. The gradient is negative so the line slopes down from left to right.